Задача 3[9]

Докажите, что следующие числа не рациональны

а) ; б) ; в) ;

г) ; д) ; е) .

Решение:

а) если рационально, то и рационально, а это не так;

б) также как и в а);

в) возведите число в квадрат, и докажите, что результат не рационален.

г) аналогично доказательству иррациональности ; из следует, что и и делятся на ;

Кроме корней натуральных чисел и, вообще, корней различных многочленов с целочисленными коэффициентами действительные числа содержат бесконечное множество трансцендентных чисел. Например, число , равное половине длины единичной окружности, является трансцендентным числом. Число также является трансцендентным. Трансцендентные числа — это числа, которые не являются корнями никакого многочлена с целыми коэффициентами. Доказательство того, что есть трансцендентные числа, довольно сложное и мы углубляться в эту тему не будем.

Суть в том, что действительные числа содержат все возможные длины — какой бы кусочек веревки вы не отрезали, длина его всегда будет действительным числом. Действительные числа представляют собой полноценный набор чисел, которого, кажется, должно хватить для любых нужд. Но это не так. Существует ещё одно расширение чисел — комплексные числа. В комплексных числах можно брать корни из отрицательных чисел. Комплексные числа хороши ещё тем, что любой многочлен имеет среди этих чисел корень. Например, уравнения

не имеют корней в действительных числах, зато в комплексных числах имеют.

Что такое комплексные числа? Знакомство с мнимой единицей

Число называется мнимой единицей. Можно рассматривать мнимую единицу как формальный объект, который имеет следующее свойство:

Рисунок 2. Комплексная плоскость. Каждая точка на плоскости соответствует комплексному числу. Координаты и соответствуют действительной и мнимой части комплексного числа.

Примеры вычислений с мнимой единицей:

• ;

• ;

• ;

• .

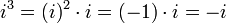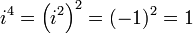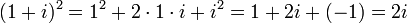Задача 4[8]

Вычислите следующие выражения:

а) ;

б)  ;

в) ;

г)  ;

д) ;

е) .

Решение

а)  ;

б) ;

в) ;

г) ;

д) ;

е) .

Определение 1

Комплексные числа  — это пара действительных чисел с заданными определенным образом операциями умножения и сложения. Комплексное число записывают как

Число называется действительной частью числа , а число  — мнимой частью числа . Их обозначают и соответственно:

Таким образом, комплексное число задается двумя действительными числами. Если интерпретировать эти числа как декартовы координаты, то получим естественное соответствие комплексных чисел и точек на плоскости (рис. 2).

Если в случае действительных чисел мы имели числовую прямую, то в случае комплексных чисел получаем числовую плоскость, которая называется комплексной плоскостью.

Задача 5[8]

Вычислите:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Решение

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Задача 6[9]

Вычислите:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Решение:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Операции сложения и умножения комплексных чисел осуществляются так, как если бы мнимая единица была переменной (а комплексные числа — многочленами от этой переменной), при этом .

Задача 7[9]

Докажите, что любой многочлен от можно свести к линейному двучлену .

Задача 8[8]

Вычислите: а) ; б) ; в) .

Решение

а) ;

б) ;

в) .

Задача 9[8]

Найдите комплексное число такое, что

а) ; б) ; в) ; г) .

Подсказка

Пусть

. Тогда из

следует

Задача 10[9]

Найдите два комплексных числа, сумма и произведение которых равны 2.

Задача 11[9]

Найдите сумму .

Решение: .

Подсказка:

Чему равны частичные суммы , , , ?

Задача 12[9]

Найдите .

Решение: .

Подсказка:

Чему равно ?

Задача 13[9]

Найдите все , для которых верно равенство .

Решение:

, , .

Подсказка:

.

Чисто мнимые числа

Определение 2

Число называется чисто мнимым, если .

Например, числа

чисто мнимые.

Задача 14[8]

Проверьте правильность следующих утверждений:

а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.

б) Произведение двух чисто мнимых чисел равно действительному числу.

в) Квадрат чисто мнимого числа равен действительному отрицательному числу.

г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.

Задача 15[8]

Найдите число , квадрат которого есть чисто мнимое число.

Решение

, .

Задача 16[8]

Найдите число , отличное от и , такое, что .

Решение

и .

Задача 17[9]

Найдите число, отличное от , куб которого которого равен .

Решение

и .

Задача 18[10]

Найдите (отметьте) на комплексной плоскости все числа , квадрат которых равен

a) чисто мнимому числу;

б) действительному числу;

в) действительному положительному числу.

Решение:

а)  — две пересекающиеся прямые , ;

б) или  — две пересекающиеся прямые , ; в)  — одна прямая .

Cопряженные числа. Модуль. Деление

Cопряженные числа

Определение 3

Пусть

Тогда число

называется комплексно-сопряженным или просто сопряженным к числу .

Комплексное число и комплексно-сопряженное к нему число отличаются знаком мнимой части, действительная часть у них одинаковая:

Задача 19[7]

Докажите, что .

Задача 20[8]

Найдите, чему равны выражения а) ;

б) ; в) для .

Решение

а) ; б) ; в) .

Задача 21[9]

Докажите тождества:

и

Задача 22[9]

Докажите, что

Подсказка Используйте задачу 21 и метод математической индукции.

Задача 23[9]

Пусть  — многочлен от . Докажите, что

Задача 24[8]

Докажите, что числа и действительные.

Задача 25[9]

Докажите, что многочлен от равный

где  — произвольное комплексное число, имеет действительные коэффициенты (если раскрыть скобки и привести подобные).

Задача 26[9]

Докажите, что если комплексное число является корнем трехчлена , где и — действительные числа, то тоже является корнем.

Задача 27[9]

Вычислите число .

Решение

.

Задача 28[9]

Найдите целые и такие, что

а) ; б) . Как отличаются ответы для а) и б)?

Задача 29[9]

Найдите целые и такие, что

а) ; б) . Как отличаются ответы для а) и б)?

Задача 30[9]

Даны числа и . Докажите, что , , целые числа при натуральном . Найдите .

Решение

. Подсказка При решении можно использовать формулу

Чему равно ?

Задача 31[9]

Число целое. Найдите его.

Решение

.

Задача 32[9]

Число целое. Найдите его.

Решение

.

Задача 33[9]

Даны два действительных числа и такие, что и  — целые числа. Докажите, что будет целым числом при любом натуральном .

Задача 34[9]

Даны два комплексных числа и такие, что и действительные числа. Докажите, что будет действительным числом при любом натуральном .

Задача 35[8]

Покажите, что

Модуль

Определение 4

Пусть . Модулем комплексного числа называется число

— длина отрезка на комплексной плоскости.

Посмотрите на рисунок 2. Модуль числа  — это длина отрезка .

Модуль комплексного числа есть неотрицательное действительное число. Модуль равен нулю тогда и только тогда, когда само число равно нулю.

Задача 36[8]

Домножьте на сопряженные следующие числа а) ; б) ; в) ; г) ;

д) ;

е) .

Задача 37[9]

Докажите тождество . Подсказка Пусть , . Запишите равенство

которое соответствует равенству

Таким образом, утверждение последней задачи равносильно следующему утверждению:

Модуль произведения комплексных чисел равен произведению их модулей.

Деление

Идея домножения на сопряженное помогает нам определить операцию деления комплексных чисел. Рассмотрим деление на примере:

Умножим и числитель и знаменатель на одно и то же число (это число, сопряженное знаменателю). Получим:

В знаменателе стоит  — действительное число. Разделить комплексное число на действительное не сложно: нужно просто действительную и комплексную часть разделить на это число. Получаем:

Алгоритм деления на комплексное число аналогичен алгоритму избавления от иррациональности в знаменателе. Например:

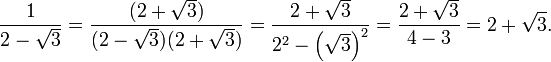
При делении комплексных чисел нужно числитель и знаменатель умножить на число, сопряженное к знаменателю. Тогда в знаменателе окажется действительное число — на него мы делить умеем: