Какие числа бывают

Прежде, чем изучать новые, комплексные числа, давайте вспомним числа, которые мы знаем. Самые простые числа — это натуральные, они обозначаются буквой :

1, 2, 3, 4, 5, 6, …

С помощью этих чисел мы считаем разные объекты. Натуральные числа мы можем складывать и умножать. Целые числа, обозначаемые , расширяют множество натуральных чисел — добавляют нуль и отрицательные числа. Наличие отрицательных чисел позволяет нам вычитать любое число из любого, тогда как «живя» в натуральных числах, при вычитании мы должны были всегда следить, чтобы из большего вычиталось меньшее. Вот примеры целых чисел:

Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы дробные числа . Их так же называют рациональными:

Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга и снова получать рациональное число (конечно, на ноль делить при этом нельзя). Следующее множество чисел, расширяющее множество рациональных чисел — это действительные (вещественные) числа .

Задача 1[8] Задача Архимеда

Докажите, что существуют иррациональные числа.

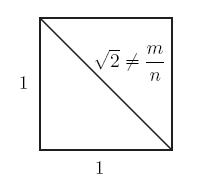
Рисунок 1. Длина диагонали единичного квадрата иррациональна

Решение.

Замечание: этот подход не является строгим в современном смысле. Нужно дать определение вещественных чисел и доказать, что среди них вообще существуют иррациональные числа. Например, в Фихтенгольце это делается с помощью Дедекиндового сечения, а уж потом доказывается, что корень из двух является примером такого числа.

Точнее эта задача звучит так: докажите, что есть отрезки, длина которых не является рациональным числом. Рассмотрим диагональ единичного квадрата. По теореме Пифагора, квадрат её длины есть

то есть

Докажем, что это число не рационально. Пусть это не так (применяем метод доказательства от противного). Тогда есть такие натуральные числа и , что

— несократимая дробь. Возведем равенство в квадрат и умножим на :

Отсюда следует, что четное, то есть , где какое-то натуральное число. Получаем:

Из последнего уравнения следует, что тоже четное число. Итак, мы получили, что и четные числа. Но вначале мы предположили, что несократимая дробь. Таким образом, получили противоречие. А значит, наше предположение, что существуют натуральные и такие, что

неверно. Конец решения.

Действительные числа очень обширны, с их помощью можно описывать любое количество вещества, любой объём жидкости, длину любого отрезка. Действительные числа можно складывать, вычитать, умножать, делить (только на ноль делить нельзя). Кроме того, можно брать корни из неотрицательных чисел и вычислять самые разные функции, например, синус, косинус, экспоненту и др. Действительные числа можно представлять в виде направленной прямой с выделенной точкой . Точке соответствует число . 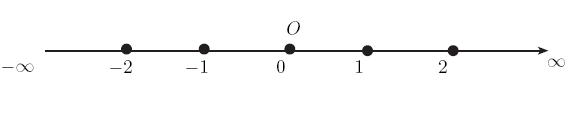Справа находятся положительные числа, а слева — отрицательные. Такое представление называется «числовой осью»:

Задача 2[8]

а) Может ли сумма двух иррациональных чисел быть рациональна? Если да, то приведите пример двух иррациональных чисел, сумма которых рациональна.

б) Приведите пример двух иррациональных чисел, сумма которых иррациональна. Докажите, что сумма действительно иррациональна.

Решение

а) ;

б) .