Переходные процессы в цепи, содержащей rlc

Переходный процесс в цепи, содержащей RLC (сопротивление, индуктивность и ёмкость) описывается дифференциальным уравнением второго порядка. Общее решение может иметь три разных вида, то есть в цепи второго порядка возможны три разных вида переходных процессов. На рисунке 55а изображена электрическая цепь второго порядка.

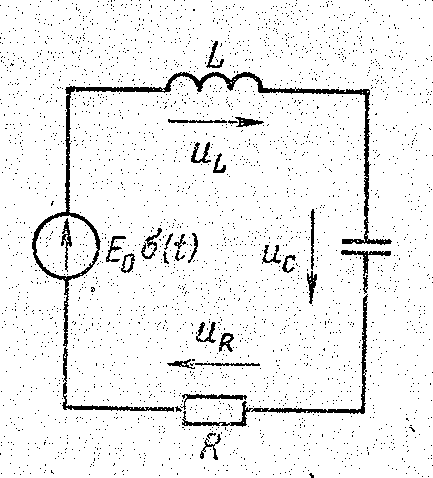
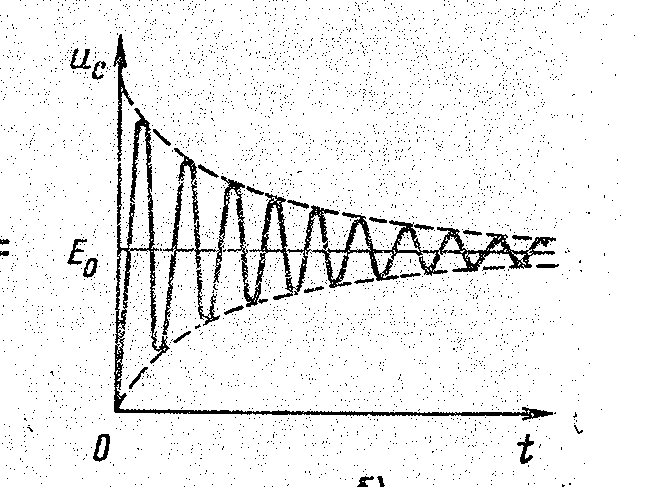
а б

Рисунок 55 Колебательный переходный процесс

ЭДС в момент времени t=0 создаёт скачок напряжения Е₀ . По окончании переходного процесса ёмкость должна зарядиться до напряжения Е₀. На рисунке 55б показан колебательный характер переходного процесса с частотой колебаний ω₀= . (Сравни с формулой для определения резонансной частоты в колебательном контуре). Колебания возникают из-за обмена энергией между ёмкостью и индуктивностью.

Характер процесса зависит от соотношения сопротивлений в контуре. Сопротивление R определяет потери в контуре. Если потери большие, то процесс быстро затухнет и будет проходить по экспоненте. Если потерь не будет R=0, то не будет и переходного процесса, будут незатухающие колебания, связанные с обменом энергиями между ёмкостью и индуктивностью. С увеличением значения R колебания начнут затухать и при каком-то значении R , первая полуволна пересечёт значение Е₀ всего один раз, снизу вверх, а дальше процесс практически закончится. Такой характер переходного процесса называется критическим. Он как бы вышел на колебательный (один раз пересёк Е₀ ), но колебательным не стал. При дальнейшем увеличении R процесс станет апериодическим и ни разу не пересечёт уровень установившегося значения Е_0. То есть, процесс будет по форме такой же, как в цепи первого порядка.

Лекция 10 резонанс в электрических цепях и беспроводная связь

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Резонанс в электрической цепи это явление в электрической цепи, содержащей участки, имеющие индуктивный и емкостной характер, при этом разность фаз напряжений и токов на входной цепи равна нулю. Это явление позволяет получить напряжение на ёмкости или индуктивности значительно больше напряжения питания (но, конечно, без увеличения мощности).

Общее условие резонанса. Для любого двухполюсника общее условие можно сформулировать в виде Im[Z]=0 (при резонансе напряжений) Im[Y]=0, (при резонансе токов) где Im[Z] и Im[Y] мнимая часть комплексного сопротивления и мнимая часть комплексной проводимости двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии. Для определения условий возникновения режима резонанса в электрической цепи нужно:

• найти ее комплексное сопротивление или проводимость;

• выделить мнимую часть и приравнять её нулю.

Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости.

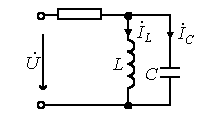
Рисунок 56 Последовательный и параллельный колебательные контура

Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром. Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным, и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резонанса это сопротивление следует учитывать, по крайней мере, как сопротивление проводников. Именно на этом резистивном сопротивлении теряется часть электромагнитной энергии, поэтому его называют сопротивлением потерь. Чем потери меньше, тем качественнее контур. Качество контура оценивается параметром, который называется добротность контура.

Последовательный резонансный контур представлен на рис. 56 слева. Напомним, что фаза индуктивного сопротивления +90⁰, а ёмкостного минус 90 градусов, тогда Комплексное сопротивление цепи равно

.

(1)

Условием резонанса из выражения (1) будет

.

(2)

Таким образом, резонанс в цепи наступает, когда индуктивное сопротивление x_L=L равно емкостному x_C=1/(C). Эти сопротивления в контуре имеются, но (и это самое важное) их сумма (векторная) равна нулю, то есть, по закону Ома, ток ограничивает только сопротивление потерь R. При резонансе сила тока максимально возможная.

Значение сопротивления при резонансе x_L= x_C=ρ называется характеристическое или волновое сопротивление контура. Отношение ρ/R=Q является добротностью контура. Частота ω_Р при резонансе называется резонансная частота и равна частоте собственных колебаний контура ω₀= , а ρ=

Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, создающий ток i=I_msint. Падение напряжения на входе уравновешивается суммой напряжений на элементах

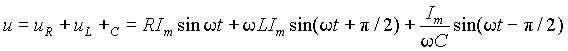. (4)

Переходя от амплитудных значений к действующим, получим напряжения на отдельных элементах контура

,

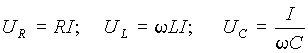а при резонансной частоте

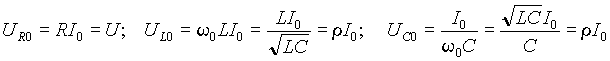, (6)

Величина обратная добротности =1/Q – называется затуханием. Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз, напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений.

Резонанс в параллельном колебательном контуре называется резонансом токов, так как эквивалентное сопротивление параллельного участка схемы равно в пределе бесконечности, то есть, цепь разорвана, и тока в резисторе нет, следовательно, на нём нет падения напряжения, и всё напряжение источника приложено к L и C. В индуктивности и ёмкости максимально возможные (по закону Ома) равные токи, векторная сумма которых равна нулю (колебания находятся в противофазе). Иначе, не будет выполняться первый закон Кирхгофа.

Как будет меняться сила тока в последовательном колебательном контуре при изменении частоты питающего напряжения? Для того чтобы кривые можно было бы сравнить между собой, значение частоты на оси абсциз приведём к резонансному значению ω/ω_р.

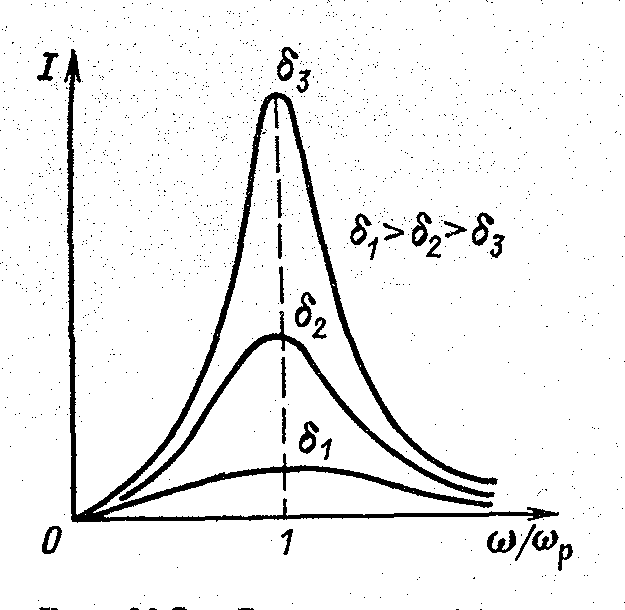
Рисунок 57 Резонансные кривые

Величина обратная добротности контура δ=1/Q называется затуханием. Из графика видно, что с увеличением добротности кривые тока становятся все более заострёнными. Если найти полосу частот, в пределах которого максимальная мощность выходного сигнала Р=I²R снижается не более чем в два раза, то с увеличением добротности этот диапазон частот становится все меньше и меньше, а значение тока для каждой кривой при этом остаётся постоянным и составляет 0,707*I_р , то есть от значения тока при резонансе. Эта полоса частот называется полосой пропускания контура. Параметр, имеющий большое значение в беспроводной связи.
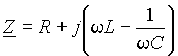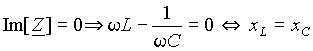