Методические указания к выполнению домашней контрольной работы № 1

Для успешного решения задач 1-5 необходимо хорошо, изучить материал раздела «Электрическое поле».

Емкость конденсатора зависит от размеров обкладок, толщины и -материала диэлектрика. Основной характеристи­кой диэлектрика является абсолютная диэлектрическая про­ницаемость , которая определяется по формуле , где — диэлектрическая проницаемость вакуума, которая .называется электрической. пос­тоянной;

— относительная диэлектрическая проницаемость данно­го диэлектрика, берется из справочных таблиц.

Пример 1

Определить емкость С плоского конденсатора, если пло­щадь каждой из его двух обкладок S=5 см². Диэлек­триком служит парафинированная бумага толщиной d=0,075 мм с относительной диэлектрической проницаемостью =4,3. Определить U — рабочее напряжение конден­сатора, если запас прочности к=3. Пробивная напряжен­ность (электрическая прочность) парафинированной бумаги E_пр= 12 кВ/мм.

Решение

1. Емкость плоского конденсатора

При подстановке в эту формулу псе величины выражены в единицах системы СИ: S=6см² = 5·10^-4 м²; d = 0,0075 мм = 0,0715·10^-3 м.

2. Пробивное напряжение конденсатора U_ар= E_пр · d = 12·0,075= 0,9 кВ=900 В.

3. Рабочее напряжение

В задачах 6—10 рассматриваются схемы смешанного сое­динения конденсаторов. Необходимость соединять имеющие­ся конденсаторы в батареи последовательно, параллельно и смешанно нередко возникает при подборе конденсаторов по емкости и напряжению.

Для решения задач 6-10 необходимо усвоить принци­пы распределения напряжения и заряда в схемах последовательного

и параллельного соединения конденсаторов; знать формулы эквивалентной емкости и энергии электрического юля конденсаторов.

В учебном пособии Частоедова в § 2.5 рассмотрен пример расчета цепи смешанного соединения конденсаторов. В том примере по заданному напряжению и емкостям всех конденсаторов определяется эквивалентная емкость батареи и напряжение на каждом из них.

Рассмотрим решение обратной задачи, когда известно спряжение на одном из конденсаторов. Пример 2

На рис. 20 приведена схема соединения конденсаторов, определить эквивалентную емкость С батареи конденсато­ров, общий заряд Q, напряжение сети U и напряжение на каждом конденсаторе, если дано: С₁=11 мкФ; С₂=15 мкФ, С₃=18 мкФ, С₄=44 мкФ; С₅ = 27 мкФ, U₃=100 В.

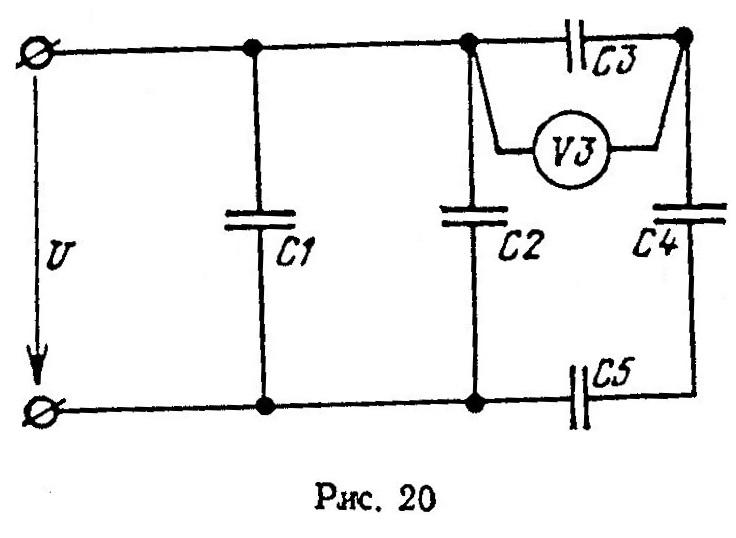
Решение

1. Эквивалентную емкость батареи определяем методом – «свертывания» цепи. Конденсаторы С₃; С₄; С₅ соединены последовательно, их общая емкость может быть определена из формулы:

конденсаторы С₁; С₂; С_3-5 соединены параллельно; эквива­лентная емкость батареи

На заданному напряжению и емкости конденсатора находим заряд, накапливаемый этим конденсатором

Кл

3. Заряд на конденсаторах С₄, С₅

Кл, т. к. конденсаторы С₃, С₄ и С₅ соединены последовательно.

4. Напряжение на четвертом и пятом конденсаторах

5. Напряжение сети (напряжение параллельных ветвей цепи)

Здесь возможна проверка:

200=100 + 33,3 + 66,7 = 200 В. .

6. Энергия электрического поля батареи

В задачах И —15 предусматривается расчет 'простой элек­трической «цепи со смешанным соединением резисторов. Для их решения необходимо знание закона Ома и первого зако­на Кирхгофа.

В учебном пособии Частоедова в § 4.4 приведен расчет цепей со смешанным соединением резисторов в общем виде. Рассмотрим решение примера.

Пример 3

На рис. 21 приведена схема соединения резисторов и ис­точника энергии. Определить эквивалентное сопротивление цепи R_экв, ток в каждом резисторе, э.д.с. Е и мощность Р

источника энергии, если известно, что R₁ = 7,5 Ом: R₂⁼21 Ом; R₃=14 Ом; R₄=25 Ом;. R₅ =17 Ом; R₀ = 0,5.Рм; U₃ = 42 В.

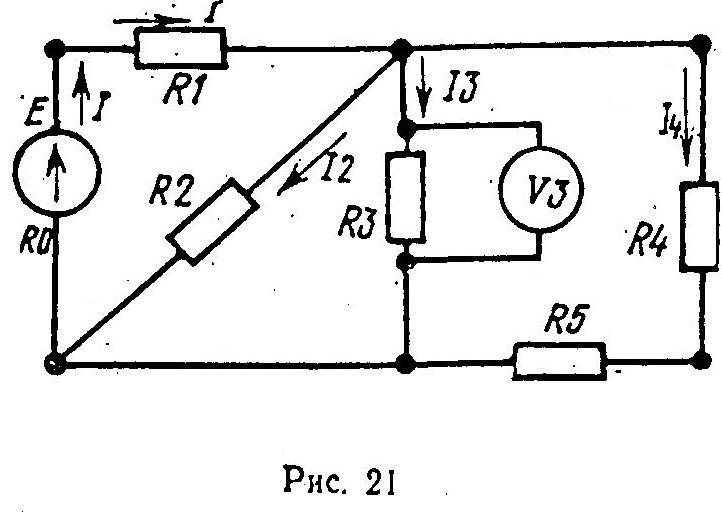
Решение

1. Обозначим стрелками направление токов в каждом резисторе. Индексы токов и напряжений на каждом резисто­ре принимаем соответствующими номеру этого резистора.

2. Эквивалентное сопротивление цепи R_экв определяем пу­тем постепенного упрощения — «свертывания» схемы:

, т. к. резисторы R₄, R₅ сое­динены последовательно:

7 Ом, т. к. резисторы R₂ R₃ R_4-5 соединены параллельно.

Эквивалентное сопротивление внешнего участка Ом, т. к. резисторы R₁, R_2-5 соединены последовательно.

3. По закону Ома для участка цепи находим токи в па­раллельных ветвях ( , т. к. резисторы R₁, R_2-5 соединены параллельно):

4. По первому закону .Кирхгофа находим ток источника

5. Эл.с. источника энергии

6. Мощность источника энергии

В задачах 16—20 должен быть выполнен расчет потенци­алов точек одноконтурной (неразветвленной) щели и после­дующее построение потенциальной диаграммы. Для решения этих задач необходимо знать правила изменения потенциала в электрической цепи и принципы построения потенциаль­ных диаграмм (учебник Частоедова, § 42).

Пример 4

Определить потенциалы точек одноконтурной электри­ческой цепи (рис. 22) и построить ш масштабе потенциаль­ную диаграмму по следующим данным E₁=60 В; E₁=28 В, R₀₁= R 02=0,75 Ом; R₁=6,5 Ом; R2=5 Ом; R₃=3 Ом.

По потенциальной диаграмме определить напряжение U_БГ

между точками Б и Г.

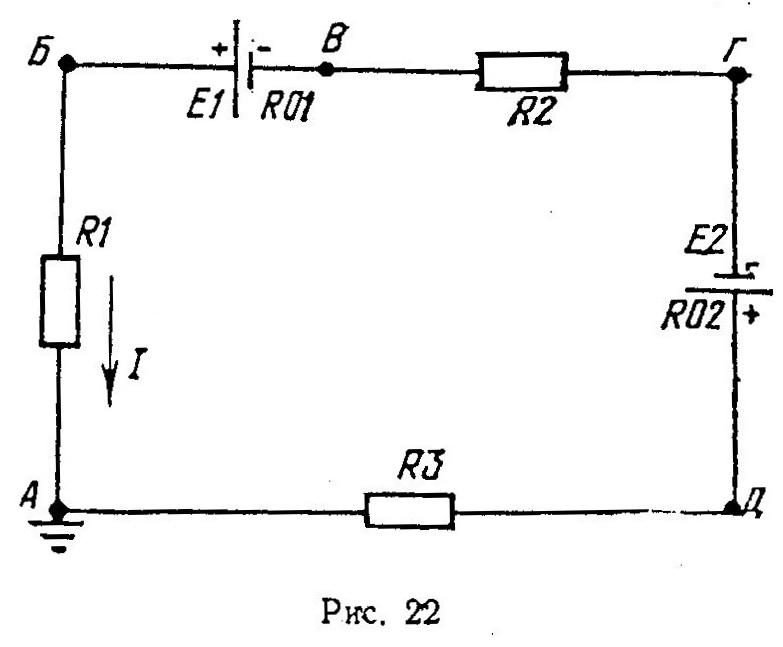
Решение

1. Ток в пели по закону Ома

Направление тока совпадает с направлением э.д.с. E₁ т. к.. E₁> E₂ покажем направление тока на схеме.

2. Для определения потенциалов точек цепи произвольно выбираем направление обхода контура: пусть направление обхода контура принято по часовой стрелке, против направ­ления тока.

3. Определяем потенциалы точек цепи. Точка А заземле­на, поэтому ее потенциал

При переходе из точки А в точку Б цепи через резистор R1 против направления тока потенциал повышается на IR1.

При переходе из точки Б в точку В через источник э.д.с. E₁ от его положительного зажима к отрицательному проис­ходит снижение потенциала на величину E₁ и одновременное повышение на IR1:

При переходе из точки В в точку Г через резистор E₂ против направления тока потенциал повышается на IR2:

При переходе из точки Г в точку Д через источник э.д.с. E₂ от его отрицательного полюса к положительному проис­ходит повышение потенциала на величину £₂ и на величину падения напряжения на внутреннем сопротивлении IR02:

При переходе из точки Д в точку А через резистор #3 против тока происходит повышение потенциала на IR03:

Полученный результат подтверждает правильность рас­чета.

її 4. По результатам расчета строим потенциальную диаграмму (рис. 23) выбрав удобный масштаб: по горизонтальной оси в масштабе m_R = 2 Ом/ом откладываем значения сопротивлений порядке обхода контура цепи; по вертикальной оси в масштабе В/см откладываем значения полученных расчетом потенциалов точек пели. Начальной точкой

потенциальной диаграммы удобно считать потенциал за­земленной точки

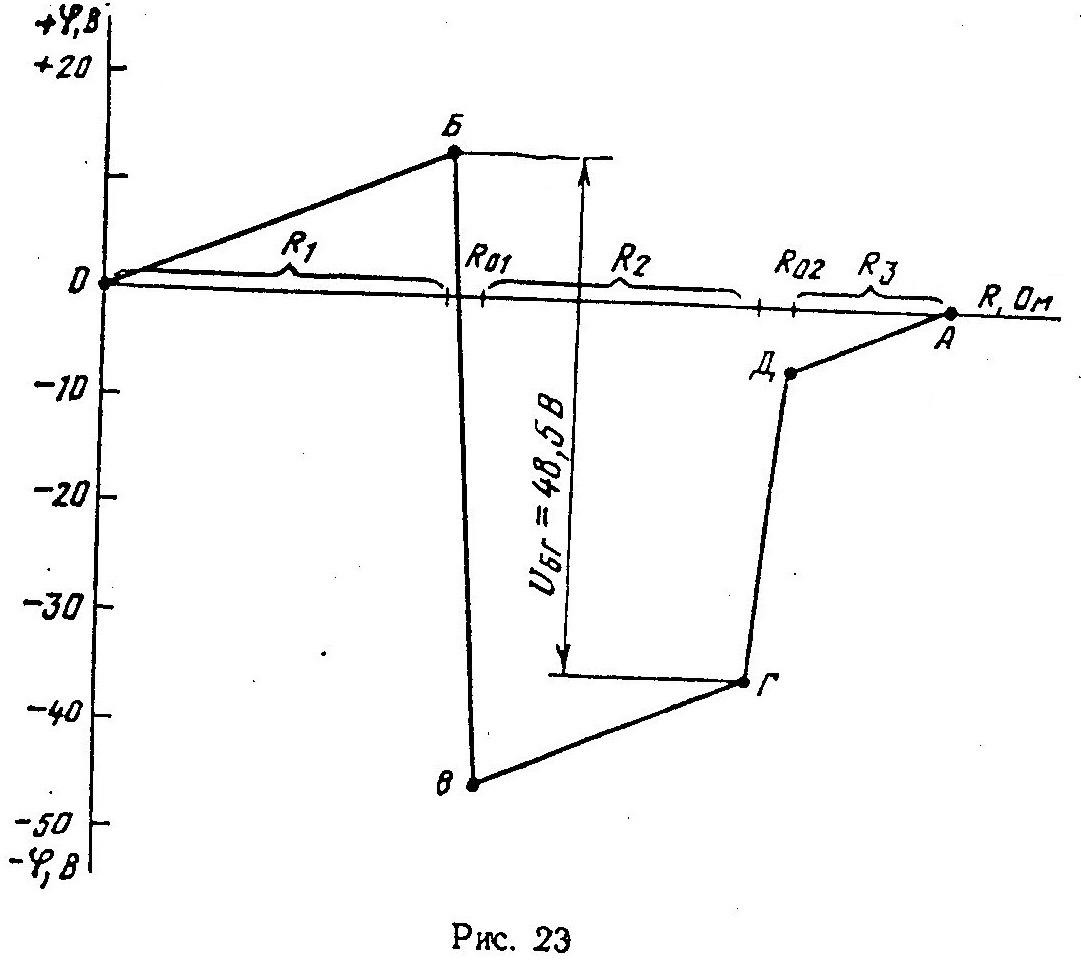
На потенциальной диаграмме графически изображено распределение потенциалов в данной электрической цепи. Пользуясь потенциальной диаграммой, можно по масштабу определить (напряжение между любыми двумя точками це­пи. Так, например, U_БГ по масштабу равно 48,5 В; это же напряжение аналитически равно

В задачах 21—25 рассматриваются принципы расчета ли­ний электропередач. Для решения этих задач необходимо изучить по учебному пособию Частоедова § 5.1; 5.2.

Пример 5

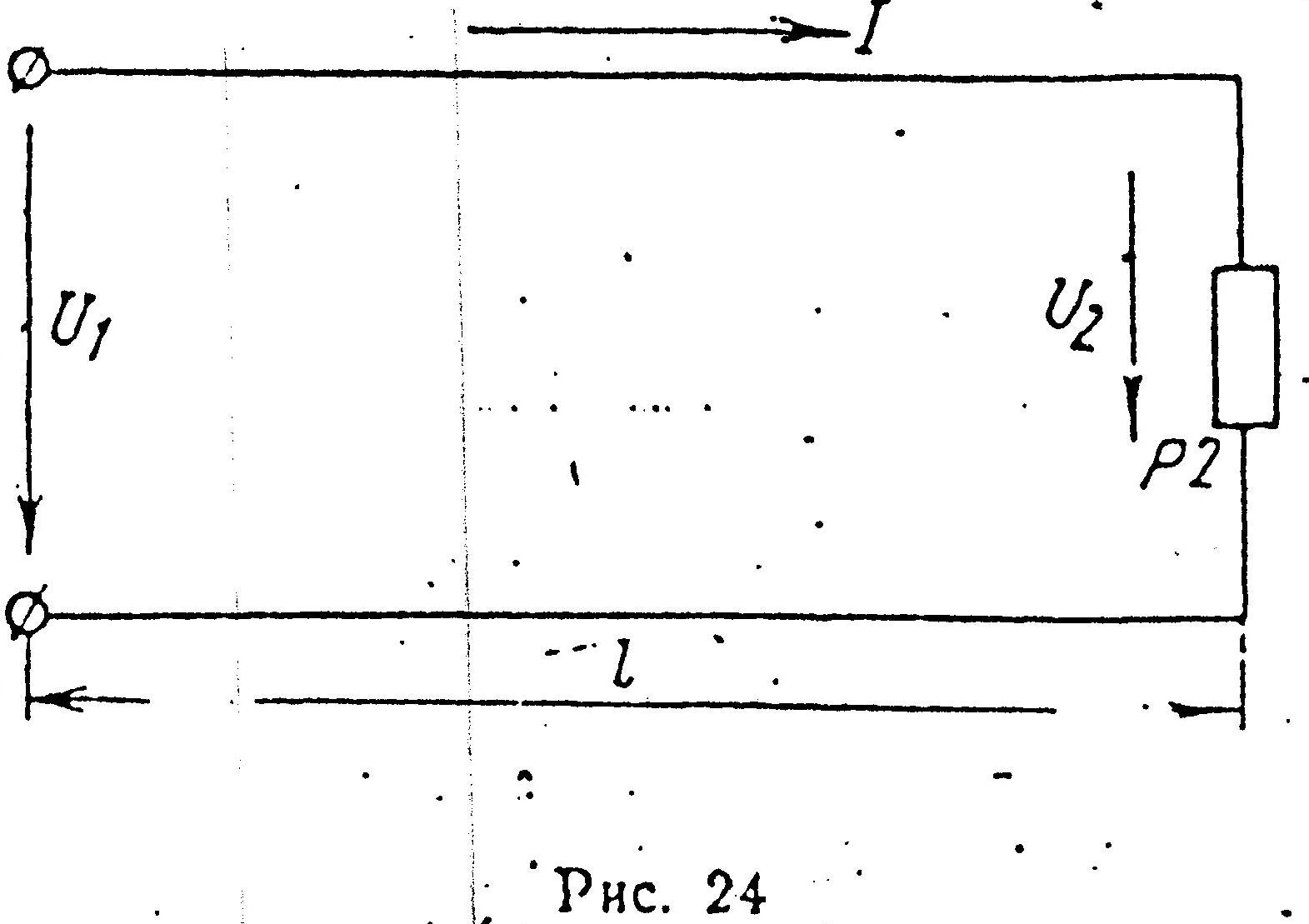
На рис. 24 изображена схема воздушной линии электро­передачи к потребителю мощностью Р₂=200 кВт; напряже­ние у потребителя U₂=220 В, длина линии l =180 м. Опре­делить ток в линии и площадь поперечного сечения прово­дов линии S, если известно, что линия должна быть, выполнена из (голых алюминиевых проводов ( ); до-

доустимая относительная потёря напряжения в линии е=10%. Выбрать стандартное сечение проводов линии; проверить его по допустимому нагреву. Определить сопротивление про­водов линии R_пр абсолютную потерю напряжения U по­тере мощности Р линии и коэффициент лолезного дей­ствия линию .

Решение

1. Ток в линии электропередачи

2. Минимальная площадь поперечного сечения проводов линии

3. Выбираем стандартное сечение проводов линии, ис­пользуя таблицу 5.1 учебного пособия Частоедова и соблюдая условие

принимаем .S=25. мм²

4. .Проверяем выбранное сечение иго допустимому нагре­ву, т. е.- то допустимому току. Из таблицы 5.1 учебного пособия Частоедова следует, что выбранное сеченне S=25 мм² . алюминиевых проводов, проложенных открыто, допускает

Ток I_доп=95 А. Т. к. I_доп =95 А>I=45_,5 А, то выбранное се­чение проходит по допустимому нагреву.

5. Сопротивление проводов линии

6. Абсолютная потеря напряжения U в линии

7. Потеря мощности в линии

8. Напряжение в начале линии

9. К.п.д линии

Задачи 26—30 предусматривают расчет сложной электри­ческой цепи.

Сложные цепи имеют несколько замкнутых контуров, электрически связанные друг с другом. В ветвях контуров имеются источники э.д.с. и резисторы, протекают разные по величине токи.

Существует несколько методов расчета сложных электри­ческих цепей.

Рассмотрим на примерах применение ряда .методов.

Пример 6

Определить токи во всех ветвях цепи (рис. 25), если э.д.с. источников энергии E₁=150 В, E₂=80 В, их внутренние со­противления R₀₁=1 Ом, R₀₂ = O_,5 Ом; сопротивления резисто­ров R₁=6 Ом, R₂=19,5 Ом, R₃ = 25 Ом, R₄=3 Ом. Задачу решить методом узловых и контурных уравнений, составлен­ных по законам Кирхгофа. Составить уравнение баланса мощностей.

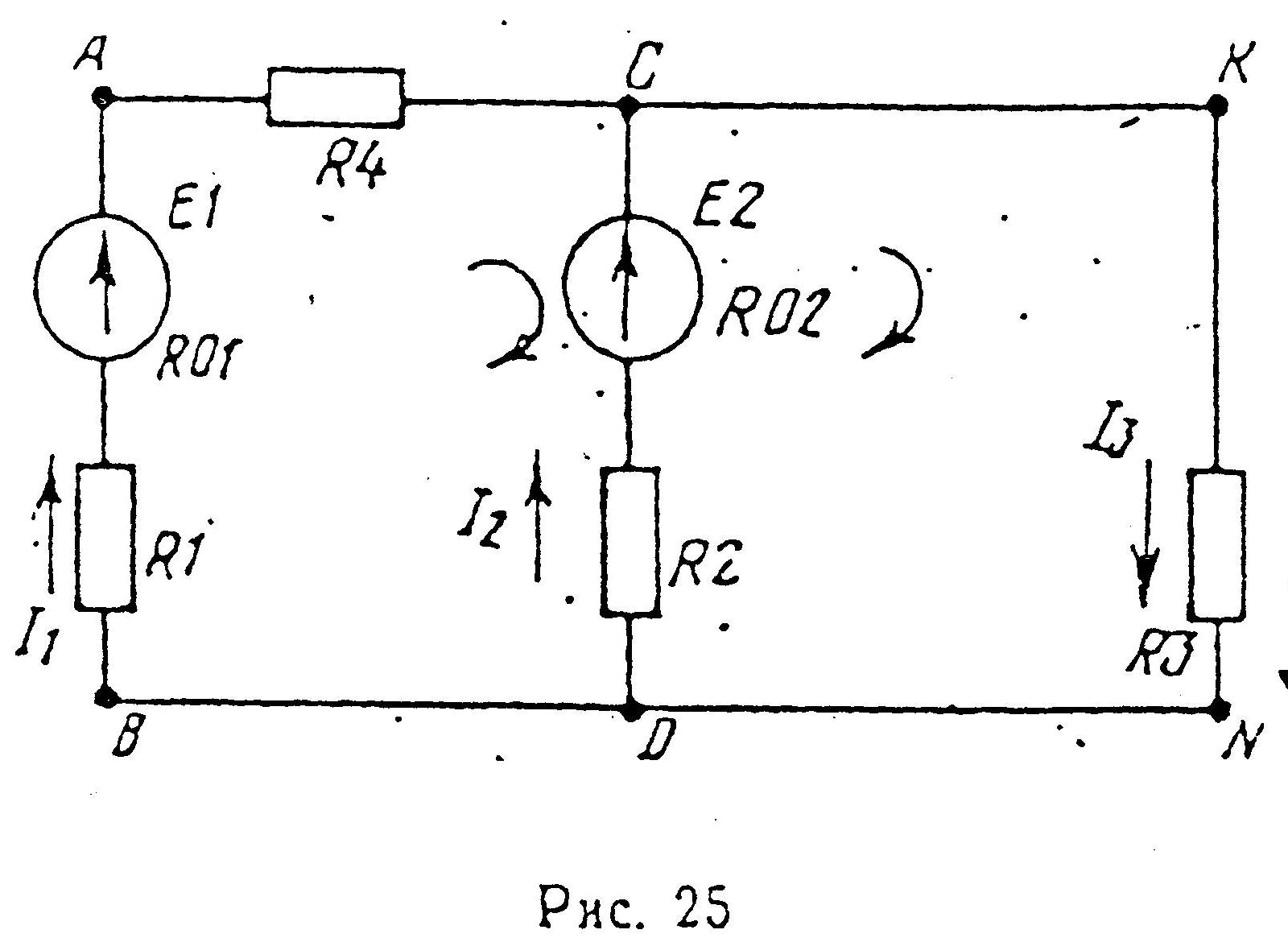
Метод узловых и контурных уравнений, составленных по законам Кирхгофа

Решение

1. На схеме произвольно показываем направления токов ветвей.

2. В задаче три неизвестных тока, для их нахождения необходимо составить систему из трех уравнений.

Первое уравнение составим для узловой точки С по пер­вому закону Кирхгофа:

второе уравнение составим для контура АСDВА по второму закону Кирхгофа; направление обхода контура при­мем «по часовой стрелке:

третье уравнение составим для контура CKNDC по вто­рому закону Кирхгофа; направление обхода контура примем «по часовой стрелке»:

3. Подставляем исходные данные в полученную систему из трех уравнений и находим значения токов ветвей:

Из второго уравнения получаем:

Из третьего уравнения получаем:

Подставляем выражения I₁ и I₃ в первое уравнение и на­ходим ток I₂:

Определяем токи I₁ и I₃: А. .

Проверка по первому закону Кирхгофа ;

Ток получился отрицательные, это значит, что первона­чально произвольно принятое 'направление тока I₂ от точки D к точке С оказалось неверным и должно быть изменено на противоположное. При этом ток I₂ будет направлен про­тив направления э,д.с. E₂, следовательно, источник с э.д.с. E₃ находится в режиме потребителя.

Пример 7

Определить токи во всех ветвях цепи (рис. 25) по исход­ным данным примера 6 методом наложения.

Метод наложения

Решение

1. Оставляем в схеме только источник с э.д.с. E₁; источ­ник с э.д.с. E₂ исключаем, его внутреннее сопротивление в схеме остается (рис. 26).

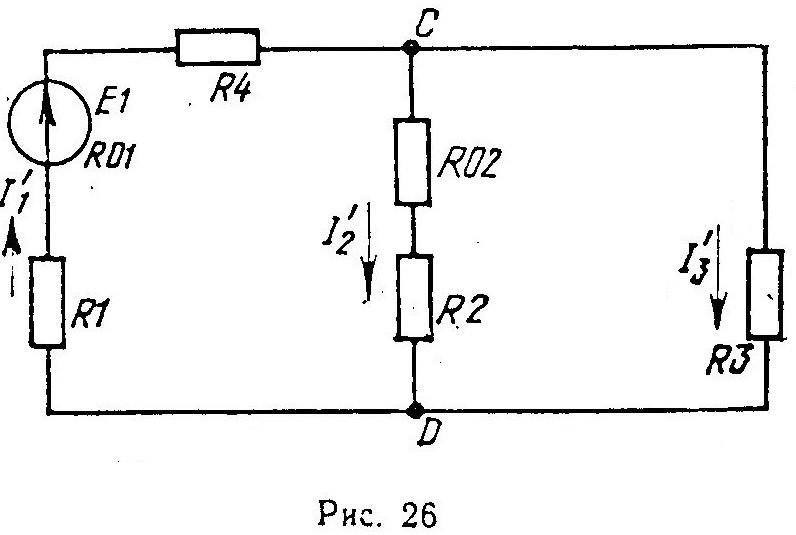
Рассчитывая получившуюся простую схему со смешан­ным соединением резисторов находим токи ветвей схемы, создаваемые источником с э.д.с. E₁:

эквивалентное сопротивление цепи (.рис. 26)

Ток первой ветви

Напряжение между точками С и D в схеме (рис. 26)

Токи второй и третьей ветвей

Показываем на схеме (рис. 20) направления полученных токов. Проверка по первому закону Кирхгофа: