Терминология и обозначения.

Теория программирования строится на основе таких разделов математики как теория множеств и теория графов. Используя базовые положения этих разделов, определим функцию как множество упорядоченных пар

1. f = {(x₁, y₁), (x₁, y₁), .....},

таких, что если

(x_i, y_i) є f, (x_j, y_j) є f и (x_i = x_j), то (y_i = y_j)

Соотношение (x, y) є f равносильно соотношению y = f(x), где x – аргумент, f – функция, y – значение функции.

Множество первых элементов упорядоченных пар функции называется областью функции. Область f = {x₁, x₂, .....}

Множество вторых элементов упорядоченных пар функции называется образом функции. Образ f = {y₁, y₂, .....}

Если функция это множество, то имеет смысл применять термин пустая функция, подфункция, разбиение функции и т.д., получающийся из терминов теории множеств, замены слова «множество» словом «функция».

На виду с заданными функциями в виде (1) удобно задавать правила для вычисления второго элемента пары, если задан первый.

f = {x, y} y = x³ – x x є {1, 2, ..., 100}

Введя следующее определение программы, будем задавать программу как конечное число функций

Σ = {f₁, f₂, f₃, ...}

Каждую функцию называют командой. Каждая функция имеет свою конечную область (входные данные) и конечный образ (выходные данные).

	x
f
	y

Программа является одним из правил для вычисления её функции состояния.

Классическим способ представления программ являются схемные записи и логические схемы, которые легко отображать в графическую форму, получившую название граф-схем.

Графическое представление программы имеет широкое применение благодаря её важному преимуществу – наглядности. Граф-схема представляет собой граф, состоящий из вершин, соединённых направленными стрелками – дугами.

Различают следующие типы вершин:

Операторная или функциональная

Начальная

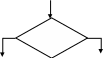
Условная или предикатная

Конечная

Объединяющая

Дуги определяют последовательность выполнения действий предписываемых вершинам, таким образом, что действие соответствует вершине, из которой стрелка исходит. Можно рассматривать граф-схему без начальной и конечной вершины.

Очевидно, граф-схема является направленным графом, и к ней применяются такие понятия как путь, цикл.

Каждая операторная вершина сопоставляется некоторому вычислительному оператору, осуществляющему преобразование значений переменных.

А условная вершина сопоставляется некоторому условию (предикату), который может быть либо истинным (Т), либо ложным (F).

Некоторые из граф-схем выделяют в качестве стандартных управляющих структур.

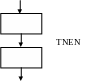
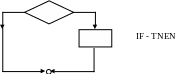
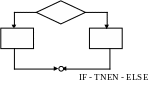
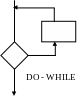
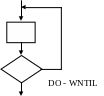
Граф-схему можно рассматривать как графическое представления выполнения и взаимосвязи операторов, которые наполняются конкретным содержимым при сопоставлении конкретных функций с операторными вершинами, а предикатов с условными вершинами. При этом в зависимости от сложности функций, связываемых с функциональными вершинами. Различают два вида граф-схем:

• операторные схемы;

• блок-схемы.

В операторной каждой функциональной вершине соответствует несложное преобразование программных переменных, которое, как правило, записывается внутри прямоугольника.

Блок-схема отображает программу на более высоком уровне, т.е. в ней операторные вершины сопоставляются с функциями и процедурами, каждая из которых может представляться отдельной блок-схемой. Операторные вершины в блок-схеме называют также блоками.

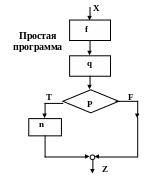
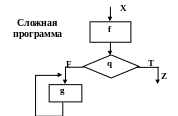
Программа называется простой, если её граф-схема удовлетворяет следующим двум условиям:

1. у неё один вход и один выход;

2. через каждую её вершину проходит хотя бы один путь от входа к выходу.

От представления программы иногда удобно перейти к её аналитическому описанию. Если программа является структурированной, это можно сделать следующим способом:

С каждой стандартной управляющей структурой связываем запись, в которой на первом месте указывается название (метка) графа управления, а дальше, в фиксированном для данного графа порядке, перечисляются предикаты, функции и множества состояний данных, относящихся соответственно к предикатным функциональным вершинам и стрелками управляющей структуры.

Запись заключается в круглые скобки и элементы записи разделяют запятыми. Такая запись называется формулой программирования.

x	f	y	g	Z

X – входные данные

( THEN, f, g, x, y, Z)

(IF-THEN-ELSE, P, f, g, x, S, R, u, v, w)

Можно не перечислять множество данных.

Рассматривая большую программу, можно выделить в ней подграфы достаточно простые и понятные по структуре. При этом всё множество граф-схем делится на 2 класса:

1. класс: к нему относятся графы, которые допускаю выделение подграфов с одним входом и выходом (рис.1) или после выполнения тождественных преобразований (рис.2).

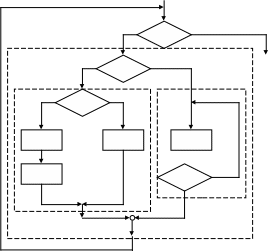
Рис. 1.

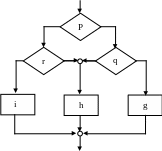
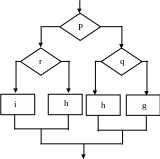
Рис. 2.

2. класс: к нему относятся граф-схемы, к которым не удаётся найти ни каких тождественных преобразований для возможности их изменения.

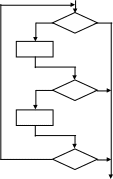
Критерий, по которому можно отнести программу к тому или иному классу, даётся в следующей теореме (теорема о разложимости):

Граф-схема разложима на элементы, соответствующие простым программам, тогда и только тогда, когда она не содержит в себе замкнутого контура с двумя или более точками выхода.

Однако существуют пути выделения структурных единиц и в таких схемах. Для этой цели необходимо ввести в рассмотрение возможность оперирования с данными, не входящими в пространство данных самой задачи. Дополнительные операции сводятся к реализации и проверке «флажков» («флажки» – произвольные проверочные условия, позволяющие изменить путь прохождения программы, не изменяя входные и выходные данные).

Одна из возможных реализаций этой идеи состоит в следующем: в дополнение к функциям и предиката исходной программы вводятся новые функции Г, П, Ф и предикат τ, которые добавляют значения Т – «истина», F – «ложь», и удаляют и выделяют эти значения во множестве входных данных.

Эти новые функции и предикат позволяют конструировать управляющую логику программы.

Теорема о структурировании:

Всякая программа эквивалентна программе, формула которой содержит не более трёх управляющих структур THEN, IF-THEN-ELSE, DO-UNTIL, дополнительные функции Г, П, Ф и предикат τ.

Для доказательства теоремы рассмотрим и докажем простую лемму.

Задаём следующие условия:

в простой программе число операторных вершин = α

число условных вершин = β

число объединяющих вершин = γ

число соединяющих эти вершины управляющих линий = δ

Лемма: в простой программе справедливо соотношение β=γ, δ=α+3β+1

Управляющие линии	вход	Операторные вершины	Условные вершины	Объединяющие вершины	выход	Общее число
Число концов (входящих)	-	α	β	2γ	1	α + β + 2γ + 1
Число концов (исходящих)	1	α	2β	γ	-	α + 2β + γ + 1

Очевидно, что число концов входящих равно числу концов исходящих и оба этих числа должны совпадать с числом соединяющих линий:

δ = α + β + 2γ + 1 = α + 2β + γ + 1 => β = γ =>

=> δ = α + 2β + β + 1 = α + 3β + 1 => лемма доказана.

Доказательство теоремы о структурировании.

Будем доказывать теорему путём индукции по числу управляющих линий в простой программе.

Считать, что исходная программа f простая.

Рассмотрим 3 варианта.

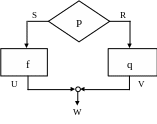
I. Первая вершина – условная.

Е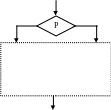 сли первая вершина условная, то блок-схема программы f обобщенно может быть представлена так (рис.1). Учитывая утверждение леммы, что β = γ для любой простой программы, введя объединяющую вершину и разобьём оставшуюся часть на составляющие программы g и h.