Нахождение оригинала по изображению

Оригинал по изображению находиться с помощью обратного преобразования Лапласа по формуле обращения.

.

Здесь а – действительное число и , где – показатель роста оригинала f(t).

Правило 1. Если изображение – простейшая дробь III типа ( ), то необходимо в знаменателе дроби выделить полный квадрат, затем представить эту дробь в виде суммы двух дробей, выполнив почленное деление, и оригиналы полученных слагаемых найти по таблице 1.

Правило 2. Если разложение знаменателя дроби содержит множителем квадратный трехчлен и , то эту дробь можно методом неопределенных коэффициентов разложить на сумму простейших дробей, найти их оригиналы и полученные оригиналы сложить.

Теорема 1. (Первая теорема разложения). Если изображение F(p) представлено рядом Лорана, те при всех p, для которых , то соответствующий оригинал является суммой степенного ряда , сходящегося при всех

Теорема 2. (Вторая теорема разложения). Если изображение есть правильная несократимая рациональная дробь , знаменатель которой имеет m различных действительных корней соответственно кратности , то оригинал этого изображения есть функция

.

Следствие: Если изображение есть правильная несократимая рациональная дробь, знаменатель которой имеет только простые корни , то оригинал определяется по формуле

.

Найти оригиналы по изображениям:

3). а) ; б) ; в) ;

4). а) б) ;

в) г)

5). а) б)

6). а) б)

7). а) ; б) ;

2. Применение преобразования Лапласа к интегрированию линейных неоднородных дифференциальных уравнений

Алгоритм решения ДУ:

. К обеим частям дифференциального уравнения применяют преобразование Лапласа, в результате чего получают операторное уравнение (другое название – изображающее уравнение) относительно изображения искомой функции.

.Операторное уравнение решают относительно этого изображения, получают операторное решение.

. По найденному изображению находят оригинал, который и является искомым решением.

Замечание: При переходе от оригиналов к изображениям используется свойство дифференцирования оригинала .

Решить уравнения:

8). . Ответ: .

9). . Ответ: .

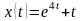10). . Ответ: .

11). Ответ: .

12). Ответ:

13). Ответ:

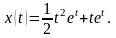
14). Ответ:

Решить системы уравнений:

15). .

Ответ:

16).

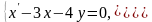
Ответ:

17). .

Ответ:

18). .

Ответ:

19).

Ответ:

20).

Ответ:

Вопросы по теме:

1. Определение оригинала

2. Определение изображения

3. Теорема о существовании изображения

4. Теорема о непериодичности изображения

5. Основные свойства преобразований Лапласа

6. Теоремы разложения ( нахождение изображения по данному оригиналу; нахождение оригинала по данному изображению)

7. Алгоритм решения ДУ и систем ДУ операторным методом