В) Ортогональні перетворення

Лінійне перетворення A евклідового простору V називається ортогональним, якщо воно зберігає скалярний добуток векторів, тобто якщо x, y V (Ax, Ay) = (x, y).

Це означає , що ортогональне перетворення зберігає довжини векторів та кути між ними (тому ортогональні перетворення іноді називають ізометричними).

Ясно, що ортогональне перетворення переводить довільний ортонормований базис в ортонормований і навпаки.

Властивості:

1. , тобто .

Дійсно, якщо A - ортогональне перетворення і - спряжене до нього перетворення, то x, y V

(x, y) = (Ax, Ay) = (x, A^*( A y)) = (x, A^* A y).

Значить, або . Із отриманих рівностей видно, що ортогональне перетворення завжди не вироджене.

2. Перетворення обернене до ортогонального, теж ортогональне.

Дійсно, якщо , то .

Сума ортогональних перетворень, взагалі кажучи, не буде ортогональним перетворенням.

2. Добуток ортогональних перетворень є ортогональним перетворенням.

Дійсно, .

Матриця A, для якої A' = A^-1, називається ортогональною матрицею.

2. Визначник ортогональної матриці дорівнює .

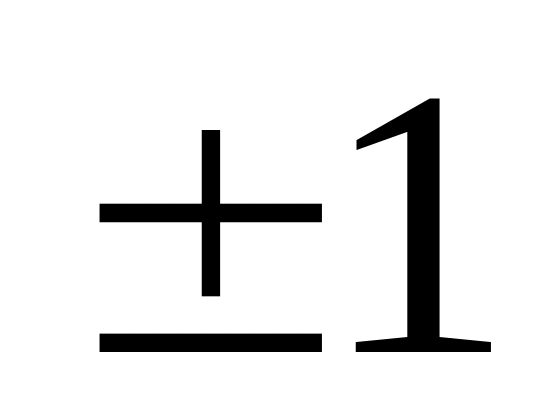Дійсно, із AA' = E випливає: |AA'| = |A||A'| = |E| = 1.

Оскільки |A| = |A'| (транспонування не змінює визначника), то:

|A|² = 1 , і .

2. Власні значення ортогонального перетворення дорівнюють .

Дійсно, якщо x - власний вектор і - відповідне йому власне значення ортогонального перетворення A, то:

(x, x) = (Ax, Ax) = (λx, λx) = λ²(x, x),

звідки, оскільки (x, x) ≠ 0, отримуємо , і .

2. Якщо підпростір інваріантний відносно ортогонального перетворення A, то його ортогональне доповнення 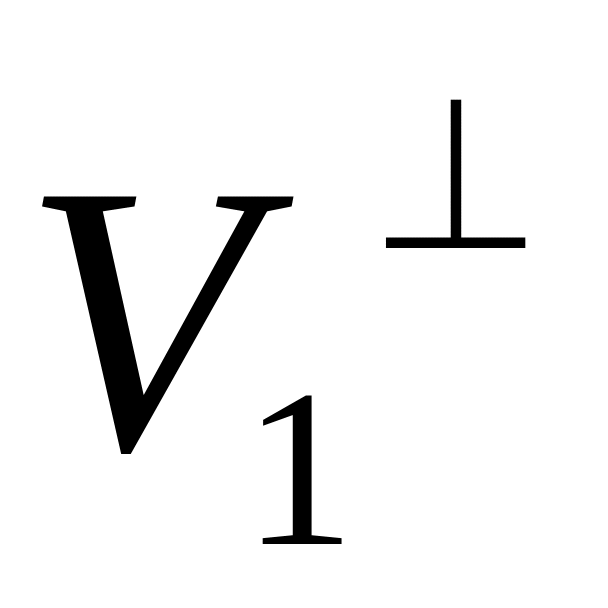теж інваріантне відносно A.

Із ортогональності A випливає . Згідно властивості 5 пункту б підпростір інваріантний відносно перетворення . Але тоді (згідно теореми 2, р.8, §2, д) цей підпростір інваріантний і відносно оберненого перетворення, тобто відносно .

Розглянемо, що являє собою довільне ортогональне перетворення.

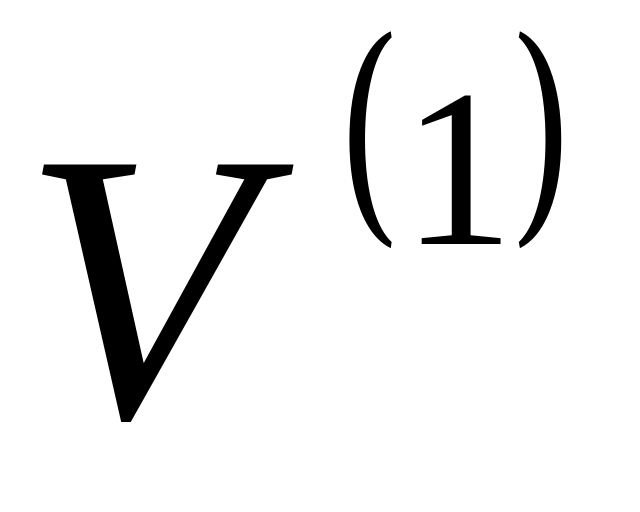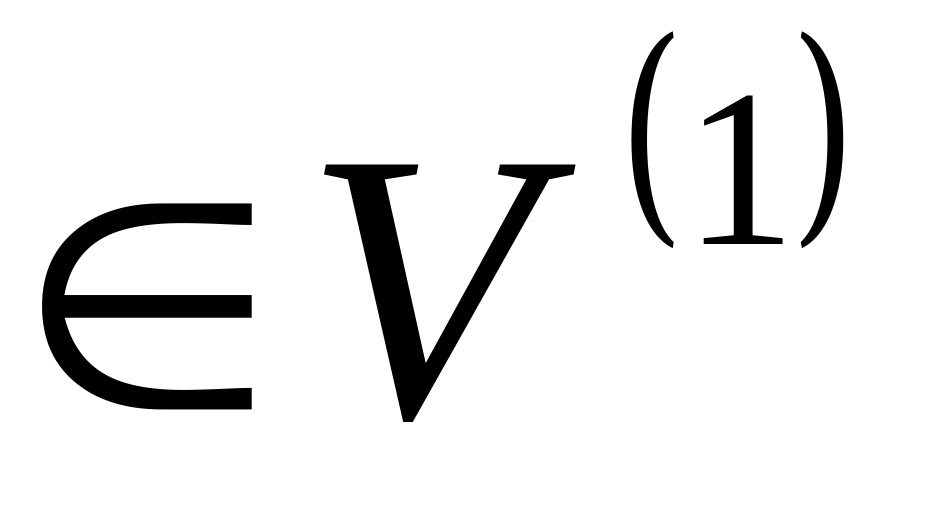1. Нехай A - ортогональне перетворення прямої і е . Тоді Aе 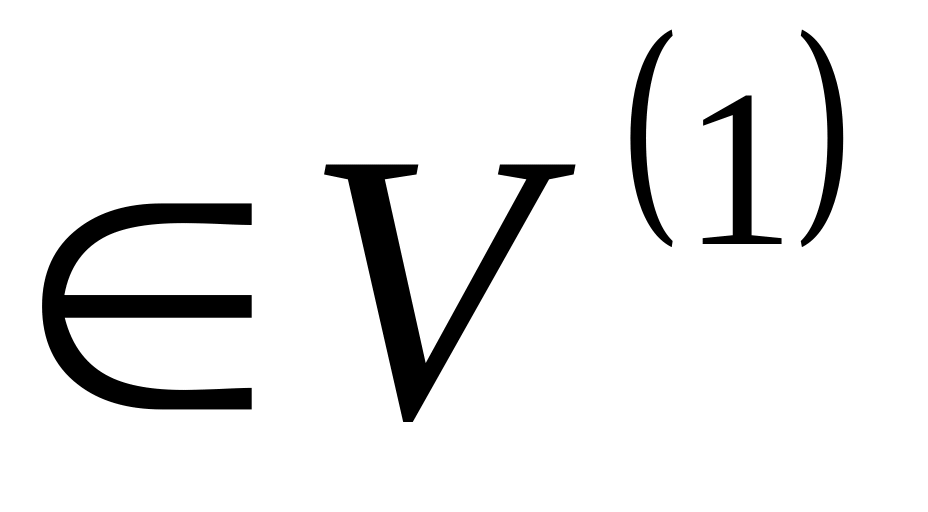і, значить, Aе = λе, де 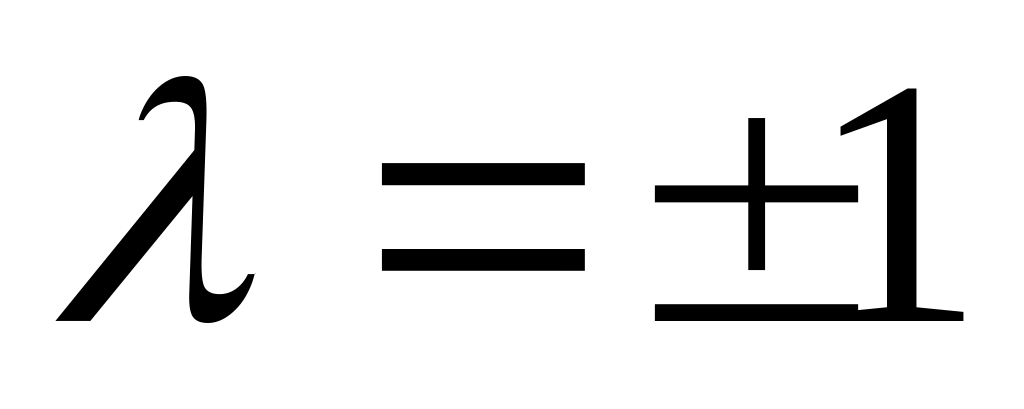, тобто Aе = ±е. Це означає, що A - або тотожнє перетворення, або центральна симетрія.

2. Нехай A - ортогональне перетворення площини, і 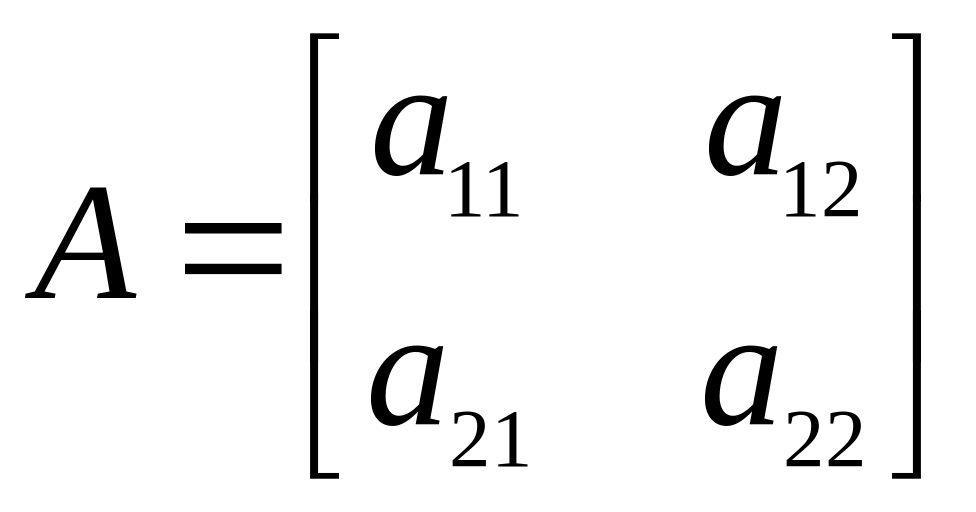- його матриця в деякому ортонормованому базисі. Тоді із 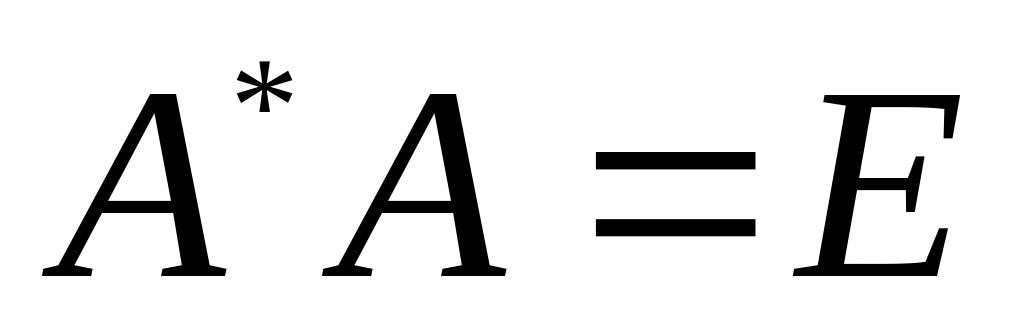, тобто 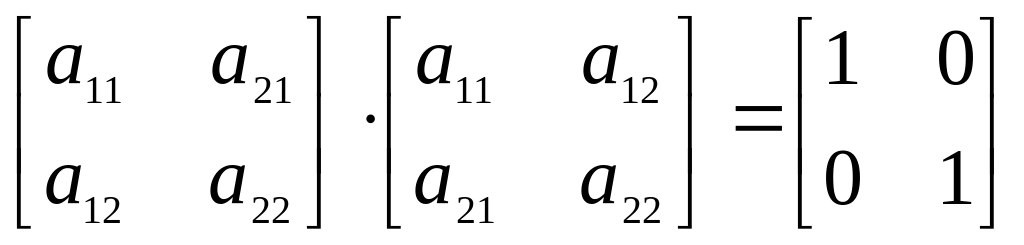, отримаємо:

,

,

.

Для перших двох рівностей знайдуться такі і , що:

, , , .

Тоді третя рівність дає , звідки випливає, що або , тобто або .

В першому випадку

,

і ми отримаємо: , тобто перетворення A - це поворот на кут навколо початку координат.

В другому випадку , і .

Ця матриця – симетрична, значить, ортогональне перетворення A є і самоспряженим, тобто в деякому ортогональному базисі його матриця зводиться до діагонального вигляду: , де .

Визначник цієї матриці повинен бути рівним:

,

значить і мають різні знаки, тобто матриця оператора А зводиться до вигляду .

Це симетрія відносно прямої, яка визначається вектором е₁ (першим вектором нового базису).

Таким чином, ортогональне перетворення площини – це або поворот навколо початку координат на деякий кут (зокрема, тотожнє перетворення або центральна симетрія – визначник цих перетворень дорівнює 1) або осьова симетрія (визначник дорівнює –1).