Властивості:

1. .

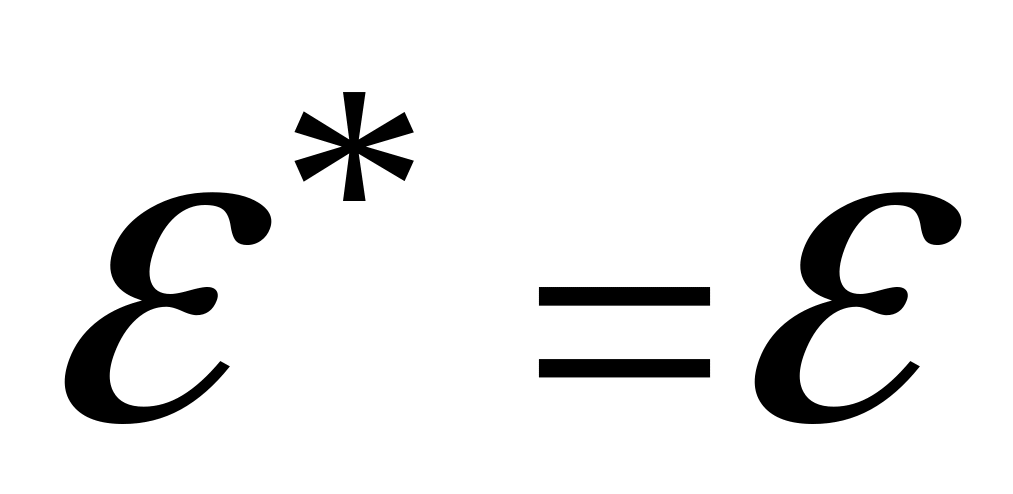Дійсно, (x, y) = ( x, y) = (x, y) = (x, y).

2. .

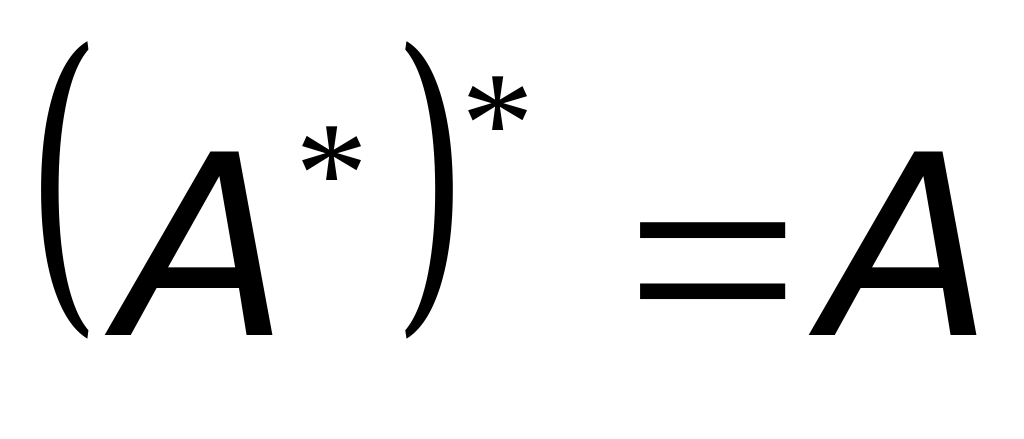Дійсно, (Ax, y) = (x, A*y) = (A*y, x) = (y, (A*)^* x) = ((A*)^* x, y).

3. .

Дійсно, (x, (A + B)*y) = ((A + B)x, y) = (Ax + Bx, y) = (Ax, y) + (Bx, y) =

= (x, A*y) + (x, B*y) = (x, (A^* + B*)y).

4.

Дійсно, (x, (AB)*y) = ((AB)x, y) = (A (Bx), y) = (Bx, A*y) = (x, B^*(A*)y) = (x, (B ^*A*)y).

5. Якщо 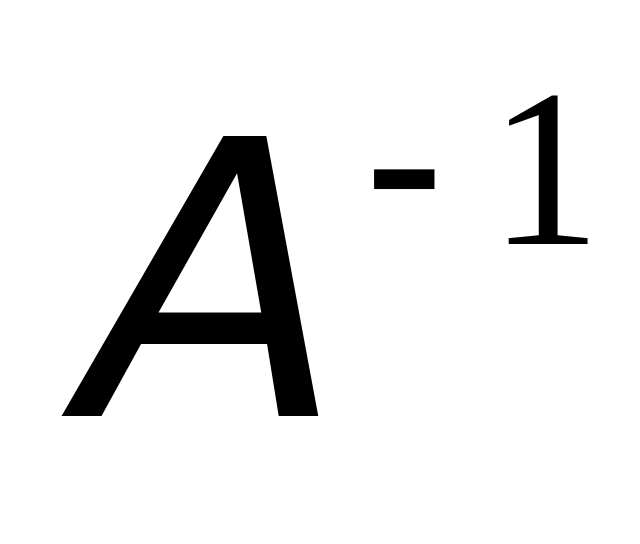існує, то .

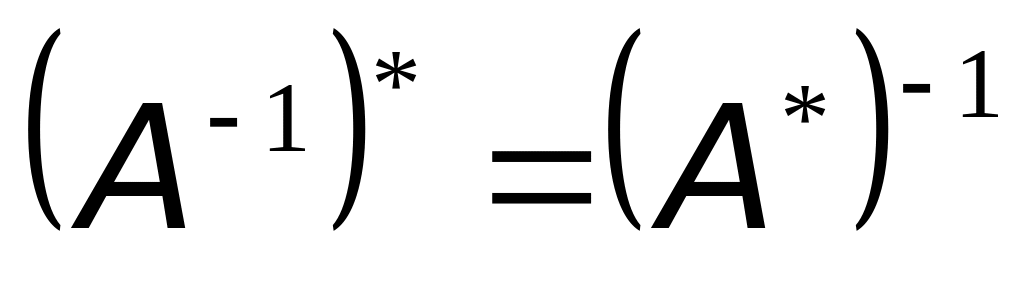Дійсно, .

Б) Самоспряжені перетворення

Самоспряженим (симетричним) називається перетворення, яке співпадає із своїм спряженим, тобто .

Якщо A – самоспряжене перетворення, то x, y V (Ax, y)=( x, Ay).

Якщо матрицею самоспряженого перетворення A в ортонормованому базисі є A=[a_ij], тоді A' = A, тобто a_ij = a_ji. Така матриця називається симетричною.

Властивості:

1. Тотожнє перетворення є самоспряженим, оскільки .

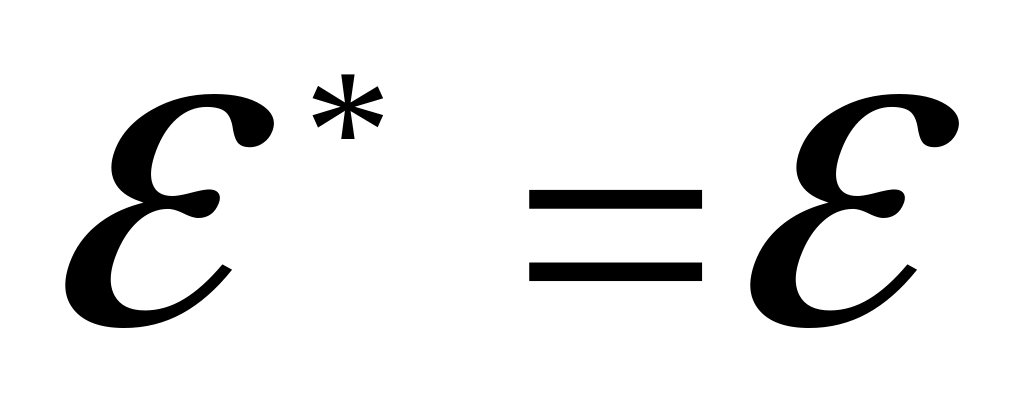2. Сума самоспряжених перетворень є самоспряженим перетворенням.

.

3. Перетворення, обернене до невиродженого самоспряженого перетворення, є самоспряженим перетворенням.

.

4. Добуток самоспряжених перетворень є самоспряженим перетворенням тоді і тільки тоді, коли ці перетворення переставні між собою.

а) якщо , і , то , тобто .

б) якщо , і , то , тобто – самоспряжене перетворення.

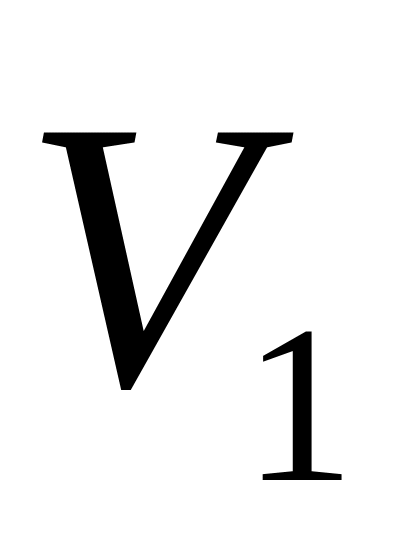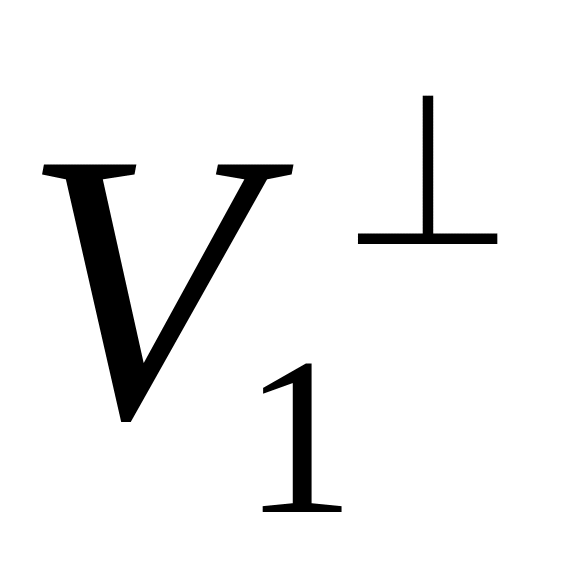5. Якщо підпростір інваріантний відносно лінійного перетворення A, то його ортогональне доповнення інваріантне відносно спряженого до A перетворення .

Нехай х – довільний вектор із , у – довільний вектор із . Тоді (A^*x, y) = = (x, Ay) = 0, оскільки Ay і, значить, х Ay. Значить, вектор A^*x , і є інваріантним відносно .

Наслідок. Якщо A – самоспряжене перетворення і підпростір, інваріантний відносноA, то і інваріантний відносно A.

6. Всі корені характеристичного многочлена самоспряженого перетворення A дійсні (власні значення самоспряженого оператора дійсні).

(Ax, х) = (λx, х),

(x, Aх) = = ( x, х).

Оскільки A – самоспряжений, то (Ax, х) = (x, Aх), значить , тобто – дійсне.

7. Власні вектори, що відповідають різним власним значенням самоспряженого оператора, ортогональні.

Нехай – власні значення самоспряженого оператора A, а х₁ та х₂ – відповідні їм власні вектори.

(Ax₁, х₂) = λ₁(x₁, х₂), (x₁, Aх₂) = λ₂ (x₁, х₂).

(Ax₁, х₂) = (x₁, Aх₂ ), бо A – самоспряжений. Тоді

(x₁, х₂) = 0 (x₁, х₂) = 0,

що й треба було довести.

8. Матриця самоспряженого оператора в деякому ортонормованому базисі зводиться до діагонального вигляду.

Нехай – одне із власних значень самоспряженого оператора A ( дійсне). Відповідний власний вектор позначимо е₁, тобто Aе₁ = λ₁е₁. Вектор е₁ можна вважати одиничним, оскільки інакше його можна замінити одиничним власним вектором з тим же власним значенням .

Позначимо через одновимірний підпростір, породжений вектором е₁. Його ортогональне доповнення буде інваріантним відносно A. Нехай – (дійсне) власне значення перетворення A в підпросторі , відповідний (одиничний) власний вектор позначимо е₂. Тоді Aе₂ = λ₂е₂. Нехай буде (інваріантним) підпростором, породженим векторами е₁ і е₂. Тоді підпростір теж інваріантний відносно A. Продовжуючи цю побудову, ми знайдемо попарно ортогональних (значить, лінійно незалежних) одиничних власних векторів перетворення A. В базисі, що складається із цих векторів, матриця А перетворення A зводиться до діагонального вигляду:

Aе₁ = λ₁е₁,

Aе₂ = λ₂е₂,

…………..

Aе_n = λ_nе_n,

звідки

А = .

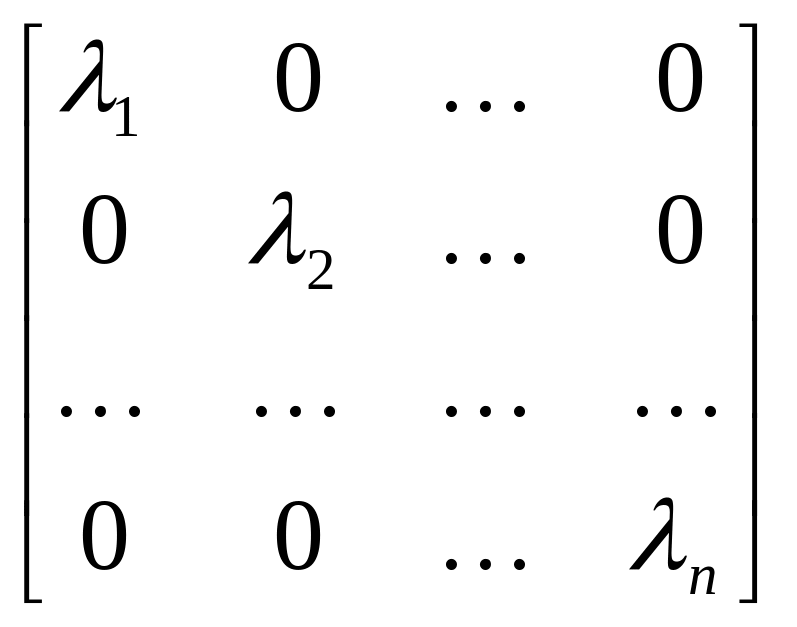Геометрично самоспряжене лінійне перетворення зводиться до розтягів з коефіцієнтами вздовж координатних осей, співнапрямлених з е₁, е_2,, …, е_n відповідно.