
- •17.5. Віддаль від точки до площини
- •§18. Пряма в просторі
- •18.1. Загальне рівняння прямої
- •18.2. Канонічне рівняння прямої
- •18.3. Рівняння прямої, що проходить через дві задані точки
- •18.4. Кут між двома прямими
- •18.5. Взаємне розміщення прямої і площини
- •§19. Криві другого порядку
- •19.1. Коло і його рівняння
- •19.2. Еліпс і його рівняння
- •19.3. Гіпербола та її рівняння
- •19.4. Асимптоти гіперболи
- •19.5. Парабола та її рівняння
- •§ 20. Перетворення прямокутних координат
- •20.1. Перенесення початку координат
- •20.2. Поворот осей координат
- •§21. Полярна система координат
§21. Полярна система координат
Н айбільш
важливою після прямокутної системи
координат є полярна система координат.
До цього положення точки на площині ми
визначали двома числами (координатами)
в прямокутній системі координат, але
це можна однозначно визначити за
допомогою полярної системи координат.
Вона складається із деякої точки
,
яка називається полюсом і променя
айбільш
важливою після прямокутної системи
координат є полярна система координат.
До цього положення точки на площині ми
визначали двома числами (координатами)
в прямокутній системі координат, але
це можна однозначно визначити за
допомогою полярної системи координат.
Вона складається із деякої точки
,
яка називається полюсом і променя
![]() ,
який виходить із цієї точки, який
називається полярною віссю (мал. 66). Крім
цього задається одиниця масштабу.
,
який виходить із цієї точки, який
називається полярною віссю (мал. 66). Крім
цього задається одиниця масштабу.
Нехай
точка М
довільна точка площини, а
![]() віддаль цієї точки від точки
,
а
віддаль цієї точки від точки
,
а
![]() це кут, на який потрібно повернути
полярну вісь для суміщення з променем
це кут, на який потрібно повернути
полярну вісь для суміщення з променем
![]() .
.
Полярними
координатами точки
називаються числа
і
.
Число
вважається першою координатою і
називається полярним радіусом, а число
- другою координатою і називається
полярним кутом. Точка
з полярними координатами позначається
так
![]()
Полярний
радіус може змінюватися в межах:
![]() ,
а полярний кут в межах:
,
а полярний кут в межах:
![]() при цьому відлік полярного кута
проводиться від полярної осі проти
годинникової стрілки.
при цьому відлік полярного кута
проводиться від полярної осі проти
годинникової стрілки.
Між координатами точки у полярній системі координат та її координати в декартовій системі існує простий зв’язок.
В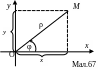 ізьмемо
вісь
декартової системи координат за полярну
вісї полярної системи, а початок
декартової системи приймемо за полюс
полярної системи координат. Нехай точка
має прямокутні координати x
та y
і полярні координати
та
(мал.67). Як видно з мал.67, маємо
ізьмемо
вісь
декартової системи координат за полярну
вісї полярної системи, а початок
декартової системи приймемо за полюс
полярної системи координат. Нехай точка
має прямокутні координати x
та y
і полярні координати
та
(мал.67). Як видно з мал.67, маємо
![]() (2.149)
(2.149)
Формули (2.149) виражають прямокутні координати через полярні.
Якщо
піднести до квадрату обидві частини
рівностей (2.149) і додати, то одержимо
![]() або
або
![]() Якщо ж поділити другу рівність на першу
в (2.149), то дістанемо
Якщо ж поділити другу рівність на першу
в (2.149), то дістанемо
![]() .
.
Формули
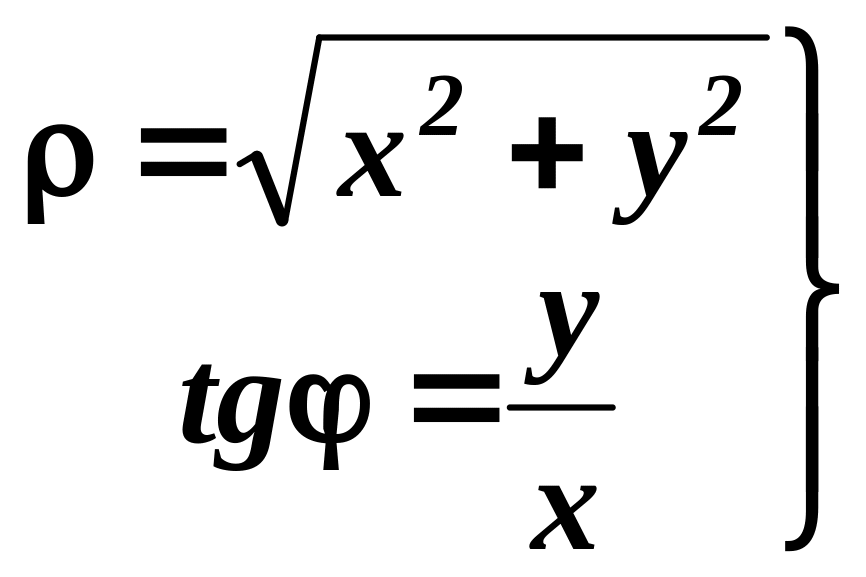 (2.150)
(2.150)
визначають полярні координати через декартові. При визначенні полярного кута слід враховувати знаки та користуючись формулами (2.149).
Приклад 1. Дано прямокутні координати точки (1;1). Знайти її полярні координати, вважаючи, що полюс суміщений з початком додатної півосі абсцис.
Розв’язування.
За формулами (2.150) маємо
![]() Згідно другої рівності
Згідно другої рівності
![]() ,
так
,
так
![]() і
і
![]()
Розглянемо деякі криві в полярній системі координат.
Спіраль Архімеда.
Ця крива
визначається рівнянням
![]()
В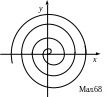 игляд
спіралі Архімеда має пружина в
годиннику(мал.68).
игляд
спіралі Архімеда має пружина в
годиннику(мал.68).
Л
 емніската
Бернуллі.
емніската
Бернуллі.
Рівняння
цієї кривої в полярній системі координат
є
![]() Графік цієї кривої зображений на мал.
69.
Графік цієї кривої зображений на мал.
69.
