19.2. Еліпс і його рівняння

Означення 2. Еліпсом називається множина точок площини, сума віддалей від яких до двох заданих точок, які називаються фокусами, є величина стала.

В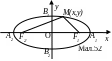 иходячи із означення 2, виведемо рівняння еліпса. Нехай задані дві точки, які називаються фокусами, і віддаль між якими позначимо через 2с (фокальна віддаль) (мал.52). Через фокуси проведемо пряму, яку візьмемо за вісь абсцис, а за вісь ординат візьмемо пряму перпендикулярну до вісі , яка проходить через середину відрізка (точка 0). Оскільки віддаль між фокусами прийняли за 2с, то координати фокусів будуть відповідно і

Нехай довільна точка еліпса. Відрізки і , які з’єднують точку еліпса з його фокусами називають фокальними радіус-векторами цієї точки і позначають і . Тоді є вели-

чина стала за означенням, позначимо її через 2а:

(2.114)

(2а>2с, тому, що в трикутнику сума двох сторін більша за третю). Покажемо, якому рівнянню задовольняють координати точки M(x,y).

Знайдемо і :

, (2.115)

. (2.116)

Підносячи обидві частини (2.115) і (2.116) до квадрату і віднімаючи, одержимо

. (2.117)

Розписавши різницю квадратів в (2.117) і враховуючи (2.114), одержимо

. (2.118)

Розглянемо систему з рівнянь (2.114) і (2.118):

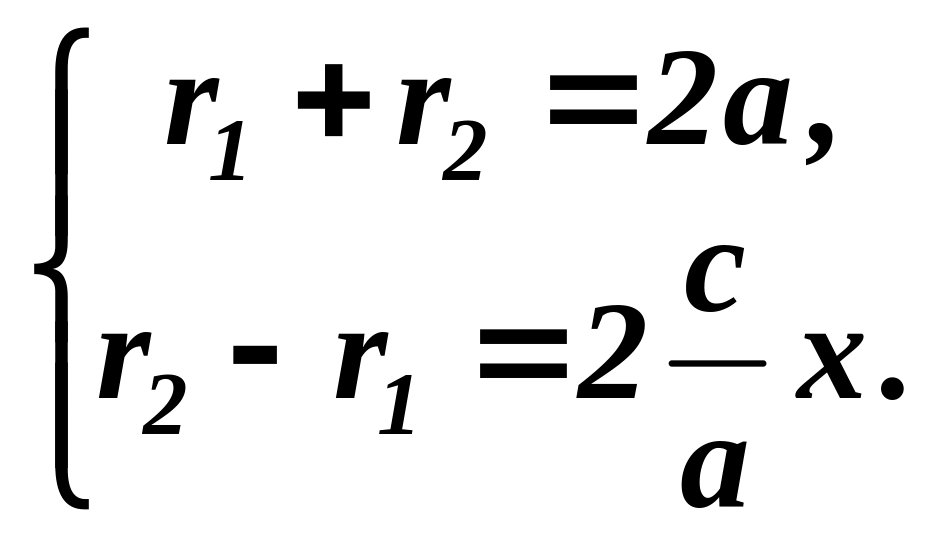(2.119)

З цієї системи знаходимо

, (2.120)

. (2.121)

Підставимо (2.121) в (2.116), одержимо , або

. (2.122)

Позначимо (2.123)

і тоді (2.122) перепишемо після простих перетворень у вигляді

. (2.124)

Рівняння (2.124) є канонічним рівнянням еліпса.

Це рівняння другого степеня, значить, еліпс крива другого порядку. Рівняння (2.124) містить і в парних степенях, значить крива, яка визначається цим рівнянням симетрична відносно осей і Осі симетрії еліпса називають його осями. Точку 0 називають центром еліпса. Із рівняння (2.124) знайдемо :

. (2.125)

Так як у, який знаходиться в першому квадранті є додатній, то

. (2.126)

З рівності (2.126) видно, якщо то і при зростанні від нуля до , спадає від до нуля.

В першому квадранті частина еліпса це дуга . Якщо провести дзеркальне відображення цієї дуги відносно осей координат, то ми одержимо весь еліпс (мал.52).

Якщо в рівнянні (2.124) то a якщо то Значить вершинами еліпса є точки Відрізок , а відрізок Ці відрізки відповідно називаються великою і малою осями еліпса. Відповідно і - велика і мала піввісь еліпса.

Означення 3. Ексцентриситетом еліпса називається відношення віддалі між фокусами до довжини великої осі.

Позначимо ексцентриситет через , то тоді

. (2.127)

Якщо , то еліпс перетворюється в коло. Підставимо (2.127) в (2.120) і (2.121), то одержимо

, (2.128)

. (2.129)

Ці формули використовуються при розв’язуванні задач.

Приклад 3. Скласти канонічне рівняння еліпса, знаючи, що велика вісь а ексцентриситет

Розв’язування. З рівняння (2.127) знайдемо . Знаючи, що А тепер знайдемо з рівності (2.123)

Підставляючи в рівняння (2.124), одержимо