§19. Криві другого порядку

Кривими другого порядку називаються лінії, рівняння яких є рівняння другого степеня відносно біжучих координат. Загальний

вигляд рівняння кривої другого порядку

. (2.109)

До кривих другого порядку відносяться коло, еліпс, гіпербола і парабола.

19.1. Коло і його рівняння

Означення 1. Колом називається множина точок площини рівновіддалених від заданої точки, яка називається центром кола.

Н ехай центр кола знаходиться в довільній точці (мал.50). Виходячи з означення 1, віддаль довільної точки площини до центра є величина стала і дорівнює . За формулою (2.3) маємо . Підносячи обидві частини цієї рівності до квадрату одержимо рівняння, яке називається нормальним рівнянням кола

. (2.110)

Вияснимо умови, при яких загальне рівняння другого степеня з двома змінними (2.109) є рівнянням кола. В цьому рівнянні А,В і С не дорівнюють нулю одночасно, тобто . Коли в рівнянні (2.110) розкрити дужки, то одержимо

. (2.111)

Щоб рівняння (2.109) і (2.111) представляли одну і ту ж лінію потрібно, щоб коефіцієнт , а всі решту пропорційні, зокрема звідси . Тепер рівняння (2.109) має вигляд

. (2.112)

Рівняння (2.112) називається загальним рівнянням кола.

Обидві частини рівняння (2.112) поділимо на і допов-

нимо члени,які містять і до повних квадратів. Одержимо

. (2.113)

Порівнюючи (2.113) з рівнянням кола (2.110) можна зробити висновок, що рівняння (2.109) є рівнянням кола при таких трьох умовах

При виконанні цих умов для кола (2.113) центр знаходиться в

точці а радіус .

Приклад 1. Привести загальне рівняння кола до нормального вигляду.

Розв’язування. Згрупуємо члени з та і доповнимо їх до повного квадрату, то одержимо , або Координати центра кола а радіус кола

Приклад 2 (економічного характеру). Два підприємства, відстань між якими 80 км, виробляють деяку продукцію, причому фабрично-заводська ціна продукції на обидвох підприємствах однакова і дорівнює Нехай транспортні витрати на перевезення одиниці продукції від підприємства до споживача складає 10грн/км, а від підприємства складає 6грн/км. Як буде розміщений ринок збуту, якщо витрати споживачів повинні бути однаковими?

Р

Мал.51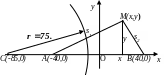

озв’язування. Осі координат проведемо через середину відрізка . Припустимо, що споживач знаходиться в точці введемо позначення (мал.51). Витрати споживача на покупку одиниці виробу з підприємства складають , а у підприємства . Витрати споживачів одинакові, якщо , або .

З мал.51 видно, що або Аналогічно або .

Для споживача витрати на покупку продукції одинакові, якщо Піднесемо обидві частини до квадрату і згрупуємо. Одержимо і, виділивши повний квадрат відносно маємо . Це нормальне рівняння кола, центр якого знаходиться на осі абсцис з абсцисою “– 85”, а радіус кола

Для споживачів, які знаходяться на цьому колі, витрати на покупку виробу одинакові. Для споживачів, які знаходяться поза колом , витрати на покупку продукції менші на підприємстві а для споживачів, які знаходяться всередині кола – на підприємстві Значить ринок буде розподілений так:

а) споживачі, які знаходяться всередині кола, будуть закупляти дані вироби на підприємстві А;

б) для споживачів, які знаходяться на колі, однаково на якому підприємстві будуть проводитися закупки;

в) споживачі, які знаходяться поза колом, будуть закупляти вироби на підприємстві В.