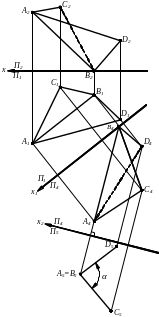
5.3. Визначення дійсної величини двогранного кута.

Визначити натуральний розмір двогранного кута при ребрі АВ – загального положення.

Аналіз: Кут між двома площинами, що перетинаються, можна побачити не спотвореним на якийсь площині проекцій, якщо площини, що утворюють кут, будуть перпендикулярні цієї площини проекцій. В такому випадку буде перпендикулярна цієї ж площини проекцій і лінія їх перетинання – ребро двогранного кута. Цю задачу зручно вирішувати, застосовуючи послідовно схеми №1 і №2 основних задач перетворення.

Задача потребує двох перетворень.

	1-ий етап П4 // AВ х1 // A1B1
	2-ий етап П5 ^ AB х2 ^ A4B4

6. Багатогранники.

Багатогранники – це геометричні тіла, утворені деякою кількістю площин, що перетинаються і являють собою замкнуті поверхні.

6.1. Завдання на кресленні.

На комплексному кресленні багатогранники задаються проекціями вершин і сіткою ребер.

Серед багатогранників в особливу групу виділяють правильні багатогранники: тетраедр, гексаедр, октаедр, додекаедр, ікосаедр, гранями яких є правильні багатокутники.

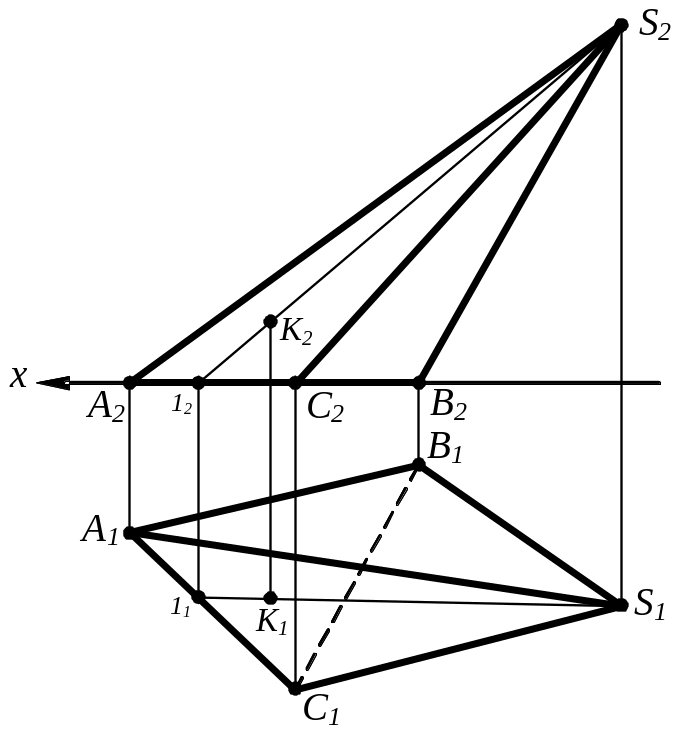
т.S – вершина піраміди, ΔАВС – основа піраміди, AS, BS, CS – ребра піраміди, ABS, ACS, BCS – грані піраміди.

Точка на поверхні багатогранника.

Точка належить поверхні багатогранника, якщо вона лежить на якийсь лінії, що належить поверхні багатогранника. Наприклад, якщо т. К лежить на поверхні багатогранника і є при цьому видимою, то вона належить грані ACS піраміди SАВС і може бути побудована за допомогою допоміжної прямої, що належить цій грані.

6.2. Перетинання багатогранника площиною і прямою.

Переріз багатогранника площиною.

Переріз багатогранника площиною являє собою плоский багатокутник, вершинами якого є точки перетинання ребер багатогранника із січною площиною, а сторонами – лінії перетинання граней багатогранника із січною площиною.

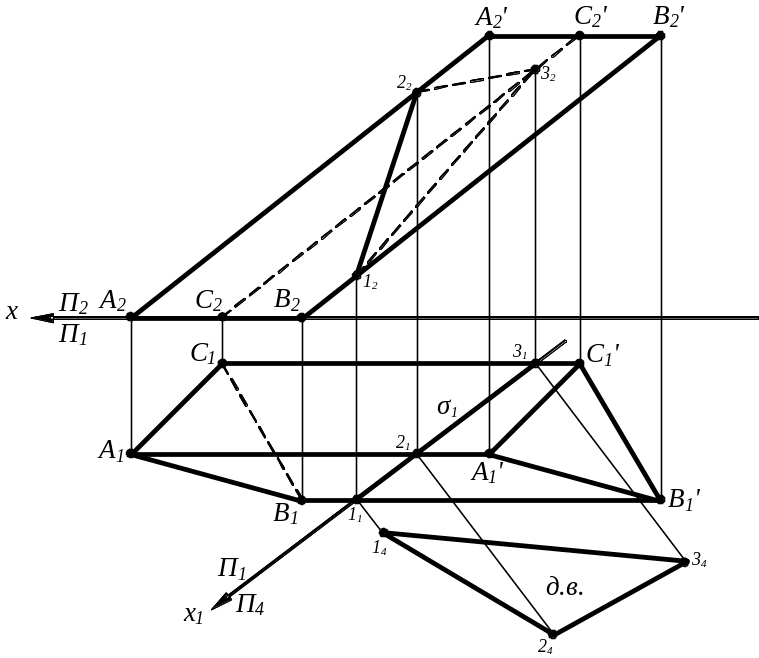
Приклад.

Побудувати проекції і істинний вигляд перерізу призми горизонтально проецюючою площиною.

Перетинання прямої із поверхнею багатогранника.

Для побудування точок перетинання прямої із поверхнею багатогранника застосовується алгоритм, що нагадує той, що використовується для визначення точки зустрічі прямої із площиною.

Алгоритм. Щоб знайти точки перетинання прямої із поверхнею багатогранника, необхідно: укласти пряму в допоміжну площину; побудувати переріз багатогранника цією площиною; точки перетинання заданої прямої із побудованою фігурою розрізу – шукані точки перетинання прямої із поверхнею багатогранника.

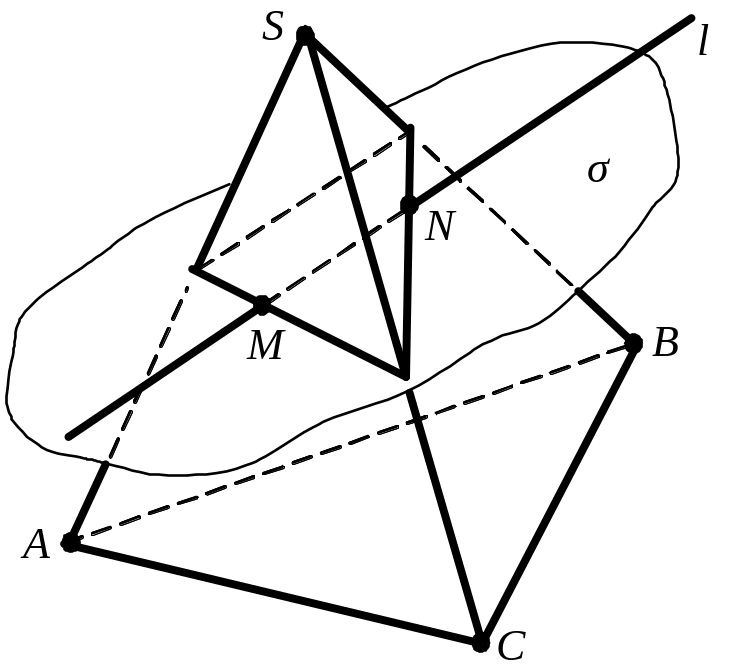
Приклад.

П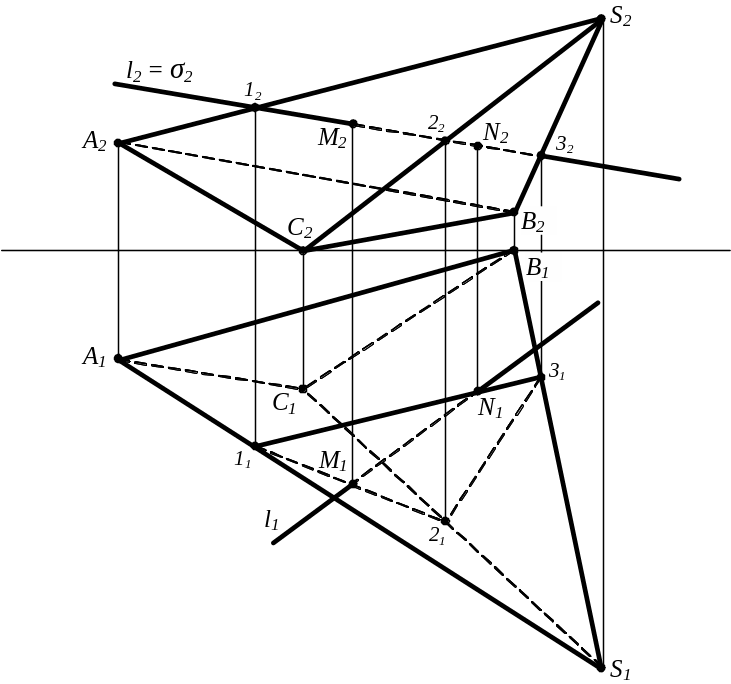 обудувати точки перетинання прямої l із поверхнею піраміди. Визначити видимість прямої.

6.3. Розгортка багатогранника.

Розгорнути поверхню – це значить, сполучити її всіма точками з площиною. Для того щоб побудувати розгортку багатогранника необхідно знати натуральні розміри (дійсну величину) ліній, що визначають її контур.

Приклад.

Побудувати розгортку піраміди SABC.

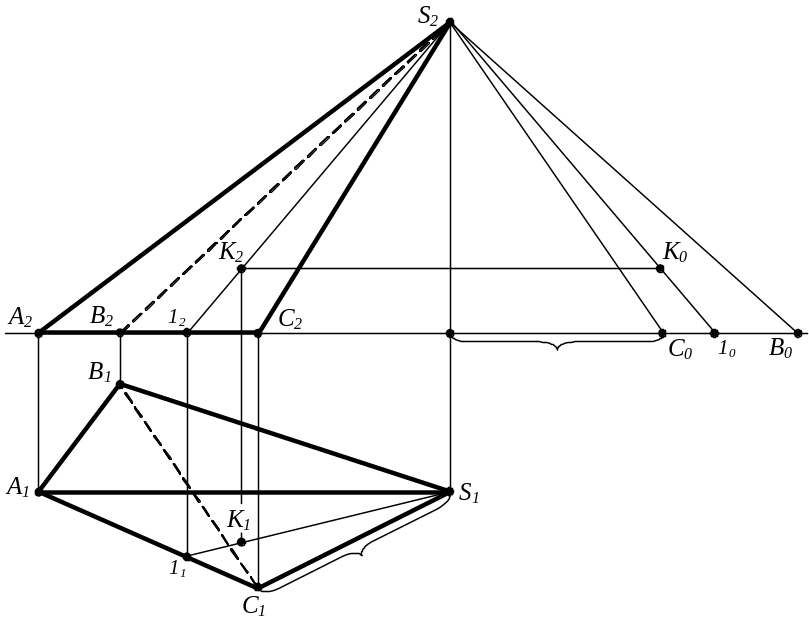
У даному випадку основа піраміди ∆ABC лежить у горизонтальній площині рівня, отже, проецюється на горизонтальну площину проекцій (П₁) без спотворення. Ребро AS паралельно площини П₂, тому A₂S₂ – натуральний розмір цього відрізка. Для розв'язання поставленої задачі необхідно визначити натуральні розміри ребер BS і CS. Тут зручно використовувати засіб прямокутного трикутника. Натуральні розміри ребер піраміди являють собою гіпотенузи прямокутних трикутників, у яких один спільний катет дорівнює різниці координат "z" вершини піраміди S і кінців ребер – точок В і С, а другі катети рівні горизонтальним проекціям відповідних ребер.

Щ об побудувати на розгортці точку, що належить поверхні багатогранника, необхідно "прив'язати" її до поверхні за допомогою якоїсь лінії, що належить цій поверхні, і перенести цю лінію на розгортку з урахуванням її натурального розміру, що дозволяє виміряти відстань до шуканої точки від якоїсь іншої вже відомої точки.