11.1. Побудова аксонометричного креслення

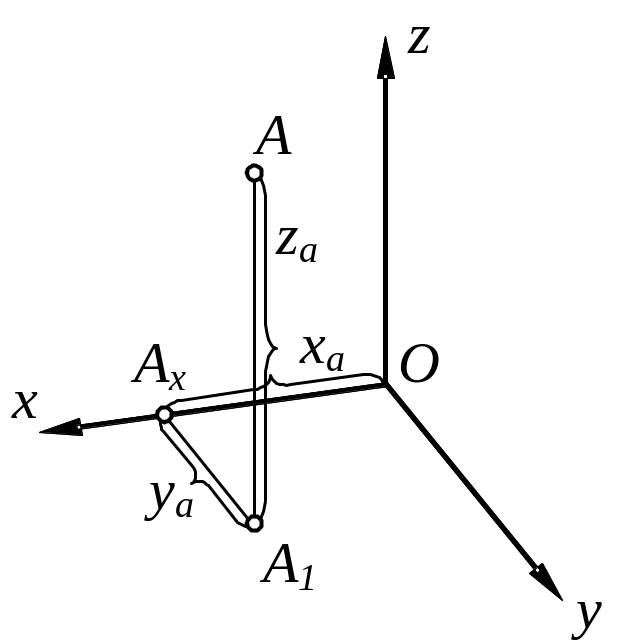
Покажемо точку А в прямокутній декартовій системі координат. Щоб звязати точку з цією системою, її проецюють на одну координатних площин.

На рисунку отримана проекція точки А1, яка має назву первинна проекція, при цьому ,як видно з рисунка одразу визначаються всі три декартові координати точки (xа, yа, zа). Ламана ОАхА1А називається координатною ламаною лінією.

С проецюємо за напрямком S на площину П (аксонометрична площина) осі координат (x, y, z), точку А, її первинну проекцію А₁ та координатну ламану лінію ОА_хА₁А. В наслідок отримали на площині П : x, y, z – аксонометричні осі; А – аксонометрична проекція точки А; А₁ – вторинну проекцію точки А; ОА_хА₁А – аксонометричну проекцію ламаної лінії ОА_хА₁А.

Сукупність всіх цих проекцій на площину П і утворює аксонометричне креслення точки.

В залежності від кута, що утворюється між напрямом проеціювання S та площиною аксонометричних проекцій П¢ , розрізняють прямокутну та косокутну аксонометрію. В першому випадку кут між напрямом проеціювання та площиною аксонометричних проекцій – прямий, а в другому непрямий.

При утворенні аксонометричного креслення координатні відрізки змінюють свою величину (спотворюються). Значить, замість натуральних координат точки А(x_а, y_а, z_а), що визначаються натуральними координатними відрізками ОА_х = x_а, А_хА₁ = y_а, АА₁ = z_а, одержимо аксонометричні координати точки, що будуть визначатися аксонометричними координатними відрізками ОА_х = x_а, А_хА₁ = y_а, АА₁ = z_а .Відношення аксонометричного координатного відрізка до натурального називається показником (коефіцієнтом) спотворення:

по осі x: U = (x_а¢ / x_а);

по осі y: V = (y_а¢ / y_а);

по осі z: W = (z_а¢ / z_а).

Ми бачимо, що спотворення за всіма трьома осями залежить від кута φ – між направленням проеціювання S та площиною аксонометричних проекцій П¢.

Ця залежність задовольняє рівнянню:

U² + V² + W² = 2 + ctg²φ

В прямокутній аксонометрії φ = 90, тому це рівняння має вигляд

U² + V² + W² = 2

Цими формулами користуються для визначення показників спотворення в різних видах аксонометрій.

Якщо показники не рівні між собою, тобто маємо три різних показника U, V, W, аксонометрія називається триметрією; якщо два з них рівні – диметрією; якщо всі показники рівні, тобто маємо однаковий коефіцієнт по всіх осях аксонометрія називається ізометрією.

11.2. Прямокутна ізометрична проекція

Прямокутна ізометрична проекція утворюється при прямокутному проеціюванні предмета та звязаних з ним координатних осей на площину аксонометричних проекцій, яка нахилена під кутом однієї величини до всіх координатних осей.

Всі коефіцієнти спотворення рівні між собою U = V = W = К , тому формула залежності показників має вигляд 3К2 = 2; К = ≈ 0,82 Кути між проекціями осей також рівні між собою і складають 120°.

Таким чином при побудові ізометрії точки кожну її натуральну координату необхідно множити на 0,82. Але на практиці (див. ГОСТ 2.317-69) коефіцієнт спотворення заміняють цілим числом (приведеним коефіцієнтом), яке дорівнює 1. Така ізометрична проекція називається приведеною. Зображення предмету в цьому випадку, буде отримано збільшеним в 1/0,82 = 1,22 рази, тобто масштаб ізометричної проекції в цьому випадку буде М1,22:1.

Ізометрична проекція кола

Рівні кола, що розташовані в координатних площинах або площинах їм паралельним проецюються в рівні еліпси. Направлення осей еліпсів в прямокутних аксонометричних проекціях визначається наступним правилом:

велика ось еліпса прямокутна до проекції координатної осі, яка не належить площині кола. Мала ось прямокутна великій.

Розмір осей еліпсів в приведеній ізометрії:

ВОЕ = 1,22d; МОЕ = 0,71d, де – d діаметр кола, що проецюється.

В колах, що проецюються завжди можна вирізнити два прямокутних діаметра, паралельних відповідним координатним осям, які проецюються на аксонометричну площину в дійсну величину. Таким чином, ізометричну проекцію кола – еліпс можливо побудувати за восьма точкам.

AB = 1,22d; CD = 0,71d; EF = LK = d

Згідно ГОСТ 2.317-69 аксонометричні еліпси дозволяється замінювати овалами. Існує декілька способів побудови таких овалів. На рис. приведені ізометричні проекції кола того ж самого радіуса, що лежать в усіх координатних площинах. Криві побудовані різними методами, але всі вони рівноцінні. В усіх координатних площинах ізометричну проекцію кола можна побудувати кожним з наведених методів.

Побудова геометричних фігур в прямокутній ізометрії

П обудова аксонометричних проекцій геометричної фігури звязана з побудовою аксонометричних проекцій деякої кількості точок, які визначають цю фігуру. Тому спочатку розглянемо побудову аксонометричної проекції точки за її комплексним кресленням

М аємо комплексне креслення 6-кутної призми. Основа призми симетрична відносно осі OZ тому координати z рівні для симетричних точок, з осі OZ і починаємо побудову.