10. Розгортки кривих поверхонь.

До поверхонь, що розгортаються, відносять такі лінійчаті поверхні, дві нескінченно близьких утворюючих яких паралельні між собою або перетинаються. Серед поверхонь обертання до тих, що розгортаються відносять циліндричні та конічні поверхні. Для сфери і тора можна побудувати тільки наближені розгортки.

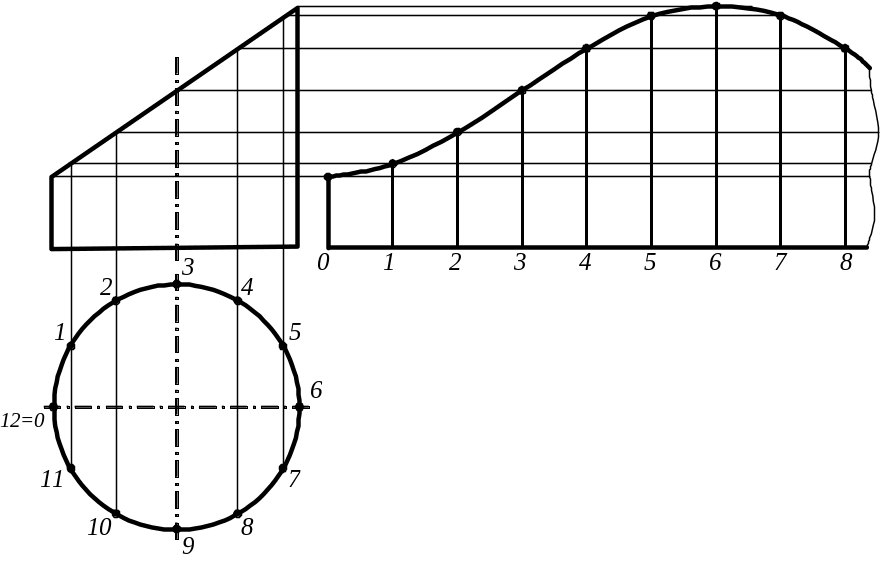
9.1. Розгортка циліндра.

Розгортка циліндра являє собою прямокутник із сторонами рівними

h = висоті циліндра,

l = довжині окружності основи

Якщо на поверхні циліндра задана лінія, яку потрібно побудувати і на його розгортці, точна розгортка заміняється наближеною, тобто будується розгортка вписаного в циліндр багатогранника – призми. Чим більше кількість граней вписаної в циліндр призми, тим ближче її розгортка до розгортки циліндра, що її охоплює.

9.2. Розгортка конуса.

Розгортка конуса являє собою сектор кола, радіус якого дорівнює довжині утворюючій конуса, а кут сектора α = 180˚.

Якщо на розгортці конуса потрібно завдати лінію, задану на його поверхні, то точна розгортка заміняється наближеною. Метод побудови наближеної розгортки в цьому випадку називається методом тріангуляції. Він полягає в тому що розгортка конуса заміняється розгорткою вписаного в нього багатогранника з трикутними гранями – піраміди. Для визначення положення точок на розгортці конуса відстані до цих точок від вершини (натуральні розміри) вимірюють по крайнім (нарисовим) утворюючим.

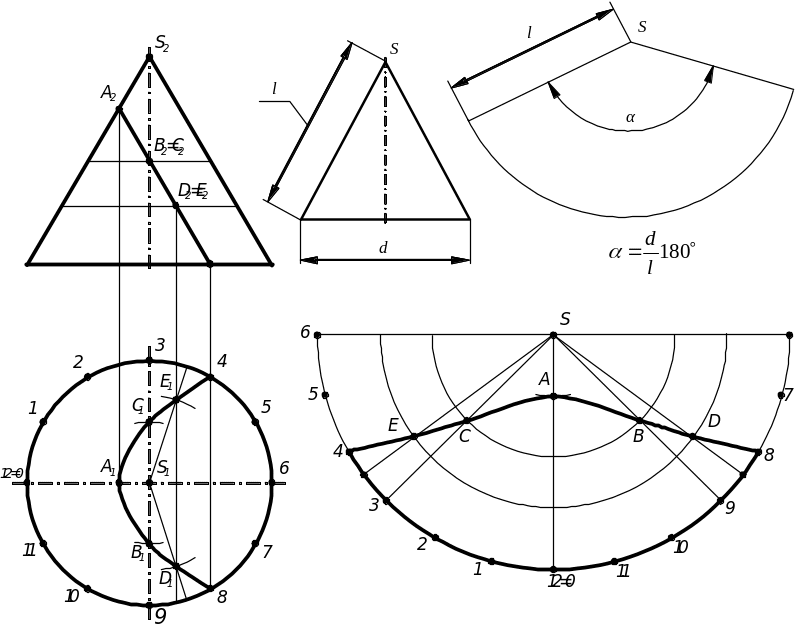
11. Аксонометрія

Прямокутні проекції дають можливість точного зображення форми та розмірів тривимірних обєктів. Недоліком цих зображень є їх недостатня наочність, бо один з трьох вимірів відсутній. Треба мати розвинену просторову уяву і досвід роботи із зображеннями на комплексному кресленні. Для полегшення сприйняття зображувальних обєктів в прямокутних проекціях, на кресленні часто додають аксонометричну проекцію, або просто аксонометрію. "Аксонометрія" – в перекладі з грецької мови "вісівимірювання" або вимірювання вздовж осі.

Аксонометричну проекцію отримують при паралельному проеціюванні обєкта на деяку площину проекцій, яка називається аксонометричною, разом з декартовою системою прямокутних координат, до якої цей обєкт жорстко привязаний.

Умови побудови аксонометричних проекцій:

1. координатні осі розташовують за основними вимірами предмета;

2. напрямок проеціювання не збігається з напрямком координатних осей та не паралельний жодній з основних координатних площин.

Основні властивості прямокутних проекцій зберігаються і для аксонометричних проекцій:

1. аксонометрична проекція відрізка прямої лінії є відрізок прямої;

2. аксонометричні проекції паралельних відрізків також є паралельні відрізки – якщо відрізки паралельні координатним осям, то їх аксонометричні проекії також паралельні координатним осям;

3. якщо точка ділить відрізок у якомусь відношенні, то і аксонометричні проекції цієї точки ділять аксонометричні проекції відрізка прямої в тому ж відношенні;

4. аксонометрична проекція кола у загальному випадку є еліпс, в окремих випадках – коло або пряма лінія.