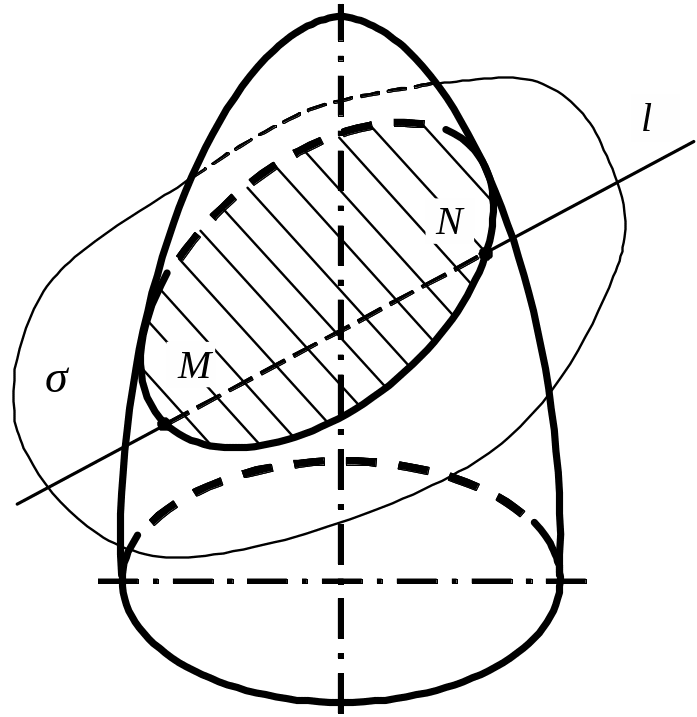
8.4. Перетинання прямої лінії з поверхнею.
Для побудови точок перетинання прямої із поверхнею застосовується той же алгоритм, що і для розв'язання аналогічної задачі з багатогранником. Розходження полягає лише у формі фігури розрізу.
Для ілюстрації обмежимося наочним малюнком.
8.5. Геометричні тіла з вирізами.
У даній темі розглянемо побудову проекцій геометричних тіл із вирізами, утвореними плоскими поверхнями. У цьому випадку задача зводиться до побудови плоских розрізів заданого геометричного тіла, які утворяться при перетинанні його з кожній із площин, що утворюють виріз.
Раніш, чим приступити безпосередньо до побудови, необхідно проаналізувавши задану фігуру, визначити, які форми розрізів повинні утворитися. Потім будують послідовно лінії перетинів, починаючи з визначення опорних точок. Закінчується розв'язання задачі визначенням видимості.
Приклад.
Побудувати 3 проекції геометричного тіла з наскрізними вирізами.
Аналіз. З огляду на розташування площин, утворюючіх виріз у заданому геометричному тілі (конусі) стосовно елементів поверхні (осі й утворюючіх), дійдемо висновку, що в даному випадку форми розрізів являють собою: коло (пл.σ ), параболу (пл.α), гіперболу (пл.ω).
9. Взаємне перетинання поверхонь.
Лінія перетинання поверхонь у загальному випадку являє собою просторову криву, порядок якої визначається як добуток порядків поверхонь, що перетинаються. У окремих випадках лінія перетинання може розпадатися на дві лінії більш низьких порядків.
Побудова лінії перетинання поверхонь може бути виконана різноманітними засобами. Найбільше універсальним із них є засіб допоміжних січних площин.
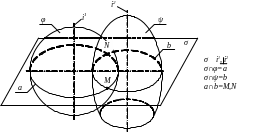
Алгоритм
Обидві задані поверхні перетинаємо допоміжною площиною, як правило, особливого положення. При цьому січні площини вибирають таким чином, щоб вони давали в перетині прості лінії: прямі або кола.
Будуємо переріз однієї з заданих поверхонь з допоміжною площиною.
Будуємо переріз другої поверхні з тієї ж площиною.
Знаходимо точки перетинання побудованих ліній переризів, що належать шуканій лінії перетинання, оскільки належать кожній із заданих поверхонь
Щоб побудувати лінію перетинання поверхонь, необхідно знайти достатню кількість точок, їй приналежних.
Побудову лінії перетинання починають із знаходження характерних (опорних) точок:
найвища і найнижча;
найближча і найдальша;
найлівіша і найправіша;
межа видимості;
точки, що лежать на характерних лініях і інші.
Приклад 1.
П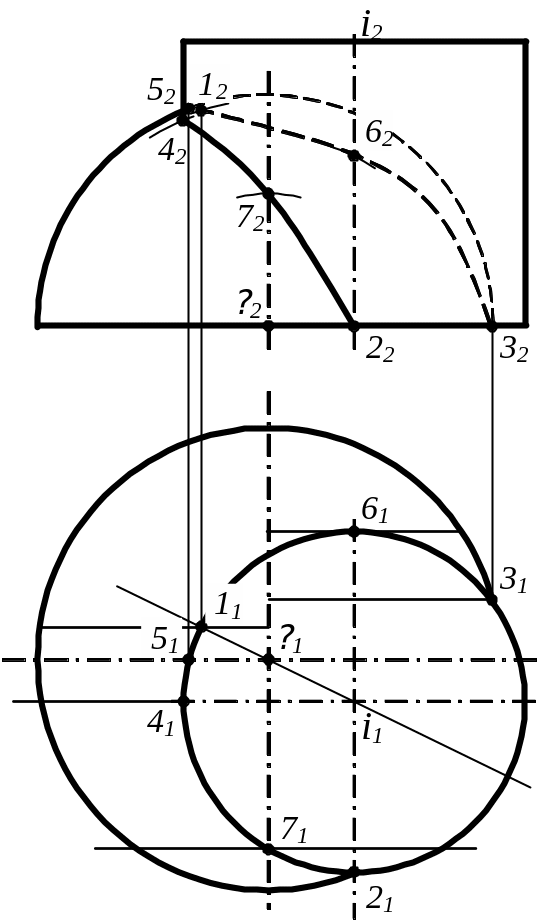
обудувати
лінію перетинання поверхонь
сфери і циліндра.
|
Цей приклад відноситься до великої групи задач на перетинання, у яких одна з поверхонь є поверхнею циліндра, вісь якого перпендикулярна площині проекцій. У цих випадках проекція лінії перетинання на цю площину збігається з проекцією самого циліндра, тобто є колом. Таким чином, задача зводиться до побудови відсутньої проекції лінії, що лежить на заданій поверхні.
|
Тут опорні точки:
т.1 – найвища – знаходиться в площині, що проходить через осі обох поверхонь, що перетинаються. У цій же площині знаходилася б і найнижча точка, якби ми мали справу із цілісною поверхнею сфери, а не з півсферою;
т.2 і 3 – найнижчі точки – лежать у спільній площині основи заданих геометричних тіл;
т.4 – межа видимості – належить нарису більш висунутої вперед поверхні циліндра;
т.5 – належить нарису сфери;
т.6 – задня.
Проміжні точки можна побудувати за допомогою допоміжних горизонтальних площин, що дають у перетинах обох поверхонь кола, або фронтальних, що дають у перетинах сфери кола, а в перетинах циліндра – прямі лінії.
Приклад 2.
Побудувати лінію перетинання поверхонь конуса і сфери.
Особливістю даної задачі є те, що обидві поверхні, що перетинаються мають спільну площину симетрії, рівнобіжну площини проекцій (у даному випадку фронтальній). У цьому випадку лінія перетинання поверхонь також буде симетрична цієї ж площини проекцій, а отже, видима і невидима половини лінії перетинання на цій проекції будуть збігатися. Звідси, кожній фронтальній проекції точки будуть відповідати проекції двох точок на горизонтальній площині, одна з яких на П2 видима, а друга – невидима. Точки перетинання нарисів поверхонь у цьому випадку обов'язково належать лінії перетинання.
Тут опорні точки:
т.1 і 2 – точки перетинання нарисів.
т.3 і 4 – межа видимості на П1 – лежать у площині екватора сфери, що розділяє сферу на верхню (видиму) і нижню (невидиму) частини.
Проміжні точки можна побудувати за допомогою горизонтальних січних площин, що дають у перетинах обох поверхонь кола.
