Определение напряжений при колебаниях. Резонанс

Колебания происходят около положения упругого равновесия, при котором в нагруженной системе имели место статические деформации и соответствующие им статические напряжения ( или — в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения . Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.

При колебаниях систем с одною степенью свободы полные деформации системы в каком либо сечении могут быть найдены путем сложения статической деформации с добавочной деформацией при колебаниях. Для проверки прочности системы, очевидно, необходимо найти наиболее опасное сечение с наибольшей в процессе колебаний суммарной величиной деформации. В простейших случаях для этого потребуется сложить наибольшую статическую деформацию с наибольшей амплитудой колебаний А, т. е.

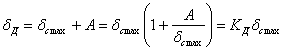
Пока система деформируется в пределах упругости, напряжения пропорциональны деформациям. Поэтому

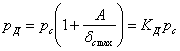
где

— коэффициент динамичности при колебаниях. Условие прочности в этом случае должно иметь такой вид:

Таким образом задача нахождения динамических напряжений и проверки прочности при колебаниях может быть сведена к определению статических напряжений и коэффициента динамичности . Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.

Как известно, дифференциальное уравнение движения колеблющегося груза Q в случае свободных колебаний можно представить в виде уравнения равновесия, в котором кроме внешней силы (веса груза Q) и силы упругого сопротивления системы учитывается также и сила инерции:

(15.13)

Здесь — координата, полностью определяющая положение груза Q во время колебаний; Р — полное упругое сопротивление системы при колебаниях; — так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние при колебаниях), которую в пределах упругости можно считать пропорциональной координате ( ); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна , то .

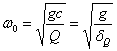Решение уравнения приводит к таким формулам для вычисления частоты и периода свободных колебаний:

и

Свободные колебания невесомого тела суть простые гармонические колебания с частотой (периодом), равной частоте (периоду) колебаний математического маятника, длина которого равна статической деформации системы от груза Q. Так, например, если груз Q растягивает призматический стержень,

при изгибе балки на двух шарнирных опорах грузом Q посредине пролета

и т.д.

Если на упругую систему, кроме груза Q и силы упругого сопротивления системы Р, в том же направлении действует периодически меняющаяся возмущающая сила S и сила сопротивления среды R, то дифференциальное уравнение движения груза Q при колебаниях также может быть представлено в виде уравнения равновесия, подобного уравнению (15.13):

(15.14)

Силу сопротивления среды R на практике в довольно большом числе случаев можно считать пропорциональной первой степени скорости колебательного движения, т. е. . Если возмущающая сила S меняется по синусоидальному закону:

,

где , а — частота возмущающей силы, то уравнение (15.14) может быть переписано так:

или

(15.15)

Здесь — так называемый коэффициент затухания колебаний, a — найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.

Решение уравнения (15.15) приводит к такому выражению для амплитуды А вынужденных колебаний при наличии сил сопротивления:

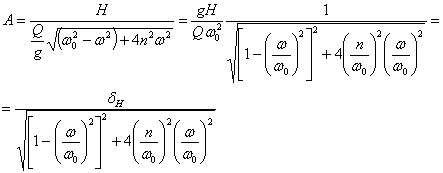
Здесь — статическая деформация системы от наибольшей величины возмущающей силы S ( ). Отношение амплитуды вынужденных колебаний А к величине деформации называется коэффициентом нарастания колебаний :

Таким образом, для динамического коэффициента получает теперь такой вид:

В этом выражении не учтена амплитуда собственных колебаний системы, которая может иметь сколько-нибудь существенное значение лишь в самом начале процесса колебаний; при наличии сил сопротивления она довольно быстро уменьшается с течением времени.

На рис.15.28 приведены графики изменения коэффициента нарастания колебаний в зависимости от величины отношения при разных значениях коэффициента затухания колебаний n (отношения ). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т.е. , и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса). При резонансе амплитуда (размах) колебаний будет резко расти с течением времени. Наличие сил трения, сопротивление воздуха и т. д. ограничивают на практике рост этой амплитуды; однако она может достичь очень большой величины, значительно превышающей те деформации, которые испытывала бы конструкция под действием ускорений той же величины, но не меняющих знака.

Известен случай, когда при резонансе угол закручивания вала увеличился в шесть раз по сравнению с тем углом, который был до наступления резонанса, — это был случай поломки коленчатых валов двигателей «Цеппелина» при первом его перелете через Атлантический океан.

Таким образом, явление резонанса, если оно длится некоторое время, а не сбивается немедленно по возникновении, ведет к постепенному росту деформаций и пропорциональных им напряжений в конструкции, что может вызвать поломку. Поэтому, как правило, при проектировании конструкций, испытывающих переменные ускорения с постоянным периодом, необходимо избежать возникновения явления резонанса.

Так как период раскачивающих (возмущающих) сил обычно является заданным, то в распоряжении проектировщика остается лишь период собственных свободных колебаний конструкции, который надо подобрать так, чтобы он в должной мере отличался от периода изменений возмущающей силы.

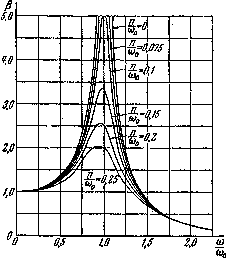Рис.15.28

С увеличением сил сопротивления явление резонанса становится все менее заметным. Заметим, однако, что силы сопротивления значительно уменьшают величину амплитуды вынужденных колебаний только вблизи от резонанса ; при других величинах отношения — влияние сил сопротивления незначительно.

Из рис.15.28 видно, что если частота изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине , коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S. При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.

Это обстоятельство имеет очень большое практическое значение; оно используется при конструировании разного рода поглотителей колебаний, сейсмографов, вибрографов и других приборов. В машиностроении амортизаторы, предохраняющие основания машин от усилий, возникающих при колебаниях, подбираются так, чтобы частота собственных колебаний машины на амортизаторах была значительно меньше частоты изменения возмущающей силы.

Колебания балки с установленным на ней массивным электромотором

Пример 1.

Рассмотрим шарнирно опертую балку с пролетом l с постоянным поперечным сечением с установленной на ней электромотором весом Q с неуравновешенной массой m_e и эксцентриситетом e. Число оборотов электромотора n об/мин. Будем исследовать напряженно-деформированное состояние в двух случаях: 1) правая опора абсолютно жесткая; 2) правая опора упругая.

Сначала рассмотрим первый случай.

Считаем, что масса электромотора значительно больше всей массы балки. Это позволяет упростить задачу, и пренебречь массой балки по сравнению с массой M электромотора, которую условно считаем приложенной в точке оси балки на расстоянии а от левой опоры (рис. 15.29, а). Для выяснения характера воздействия на балку вращающихся неуравновешенных частей рассмотрим рис.15.30.

Рис. 15.29

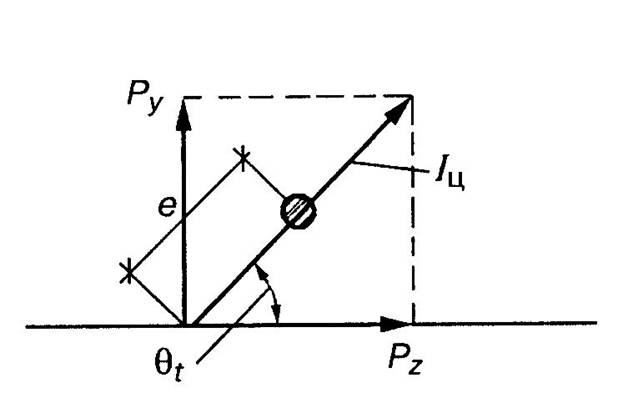
Рис. 15.30

На балку со стороны вращающейся массы m_e действует центробежная сила

(15.16)

где V – линейная скорость массы окружности радиуса е. Вычисляем угловую скорость вращения ротора по формуле

(15.17)

и линейную скорость

(15.18)

вместо (15.16), получим

(15.19)

Выразив массу через вес , вместо (15.19) получим

. (15.20)

Разложим эту силу на составляющие по осям Y и Z.

(15.21)

(15.22)

Сила вызывает изгиб балки, а продольная сила вызывает деформации растяжения-сжатия, которые в дальнейшем учитывать не будем.

Положение массы на плоскости будет определяться одним параметром – прогибом , который можно считать суммой прогибов балки при статическом действии веса неработающего мотора и прогиба балки от действия вращающейся неуравновешенной массы

. (15.23)

Запишем, используя принцип Даламбера, динамическое равновесие массы , на которую в произвольный момент времени действует сила инерции, сумма сил и упругая сила отпора балки при перемещении , равная , где - коэффициент жесткости балки в точке прикрепления мотора. Эта величина численно равна силе, приложенной к балке в этой точке и вызывающей прогиб равный единице. Можно приложить силу и определить от нее прогиб (рис. 15.31). Тогда

(15.24)

Итак

(15.25)

Рис. 15.31

Продифференцировав (15.23) дважды по времени, и учтя, что - прогиб не зависит от времени, получим

. (15.26)

Теперь вместо (15.25), получим

(15.27)

Далее учтем, что по закону Гука

. (15.28)

Поэтому вместо (15.26) будем рассматривать дифференциальное уравнение для динамической части прогиба (рис.15.29,б)

(15.29)

или

(15.30)

Обозначим (15.31)

тогда получим дифференциальное уравнение динамического прогиба балки как системы с одной степенью свободы без учета сил сопротивления

(15.32)

Это дифференциальное уравнение линейное второго порядка с известной правой частью.

В математике доказывается, что решение такого уравнения ищется в виде суммы общего решения однородного дифференциального уравнения

(15.33)

и частного решения уравнения (15.32).

Однородное дифференциальное уравнение (15.33) описывает свободные или собственные колебания упругой системы с одной степенью свободы.

Свободные колебания вызываются начальными воздействиями. Например, можно медленно отодвинуть массу от положения равновесия и затем отпустить. При этом начальные условия будут иметь вид

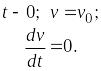(15.34)

Можно поступить иначе – толкнуть массу. При этом массе сообщается начальная скорость V₀ и начальные условия будут иметь вид

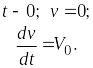(15.35)

Известно, что решение уравнения (15.33) можно рассматривать в двух формах

(15.36)

или

(15.37)

В той и другой форме участвуют две постоянные интегрирования (А и В) или , которые можно определить из начальных условий (15.34) или (15.35) или их комбинаций.

Таким образом, собственные колебания (15.37) совершаются по закону синусоиды с амплитудой А₁ и круговой частотой

(15.38)

Известно, что функции в выражении (15.36) имеют общий период .

Отсюда,

(15.39)

(15.40)

Таким образом, круговая частота собственных колебаний есть число циклов колебаний за секунд.

Коэффициент А₁ характеризует размер колебаний и носит название амплитуды колебания, - начальная фаза колебаний.

Найдем частное решение (15.32), учтя, что функция имеет вид (15.21).

Обозначим амплитуду возмущающей силы

(15.41)

Ищем частные решения уравнения

(15.42)

в виде (15.43)

Найдем производные по времени

(15.44)

(15.45)

и подставим (15.43), (15.44), (15.45) в (15.42)

откуда (15.46)

Преобразуем

,

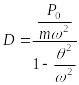Учитывая (15.31), получим

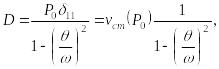(15.47)

где - величина прогиба балки от силы приложенной статическим образом.

Итак, частное решение (15.42) имеет вид

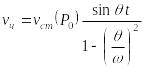. (15.48)

Таким образом, выражение динамического прогиба баки как системы с одной степенью свободы без учета сил сопротивления будет

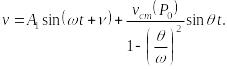(15.49)

В предыдущих рассуждениях мы не учли силы сопротивления, которые всегда возникают при колебаниях механических систем. Экспериментально доказано, что они вызывают затухание во времени собственных колебаний. Если все время действует вынуждающая сила, то изменение динамического прогиба при большом t описывается вторым слагаемым в (15.49), которое назовем вынужденным колебанием

. (15.50)

Максимальный динамический прогиб будет при

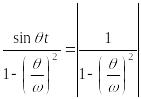. (15.51)

Обозначив

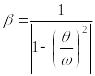(15.52)

как коэффициент нарастания колебаний, получим

(15.53)

Полный максимальный прогиб (15.23) (с учетом постоянно действующего веса электромотора) будет

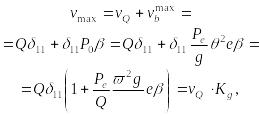(15.54)

где - (15.55)

коэффициент динамичности. Он показывает во сколько раз полный максимальный прогиб больше прогиба балки от неработающего мотора.

В случае приближения частоты изменения вынуждающей силы к частоте собственных колебаний коэффициент нарастания колебаний стремится к бесконечности (если учесть силы сопротивления колебаниям, то он стремится к большой, но конечной величине). Такое явление называется резонансом. Нужно подбирать так, чтобы не допустить резонанса в проектируемой системе.

Итак, полный прогиб во времени (15.23) будет иметь вид

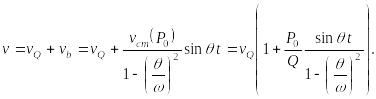(15.56)

Определим максимальные напряжения при изгибе балки в точках наиболее удаленных от нейтральной оси в процессе колебаний

(15.57)

где - (15.58)

максимальное напряжение от неработающего мотора,

- изгибающий момент от единичной силы,

(15.59)

По (15.45) и (15.46)

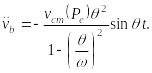(15.60)

Подставив (15.60) и (15.21) в (15.59), будем иметь

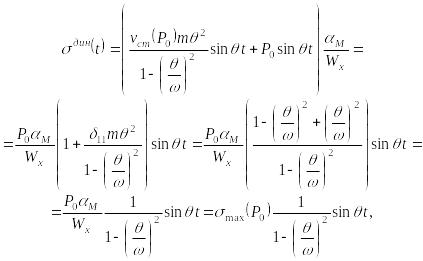(15.61)

где - максимальное нормальное напряжение в наиболее удаленной точке сечения от амплитудного значения силы , приложенной статическим образом.

Итак (15.57) примет вид

(15.62)

Максимальная величина достигается в момент соблюдения (15.51)

(15.63)

где - такой же коэффициент динамичности, который учитывается для прогиба (15.55).

Таким образом, для того чтобы определить максимальные по величине факторы, возникающие при колебаниях, нужно статические факторы умножить на коэффициент динамичности (см. формулы (15.54) и (15.63)).

Теперь рассмотрим второй случай опирания правого конца балки – упругое опирание, балка подвешена к растянутому стержню.

При этом изменится коэффициент жесткости в месте прикрепления мотора. Теперь величина будет складываться из двух слагаемых: одно за счет прогиба балки на жестких опорах (как в первом случае) и перемещения балки как жесткого диска в том же сечении за счет опускания правого конца балки из-за деформации растянутого стержня (рис.15.32)

Таким образом,

. (15.64)

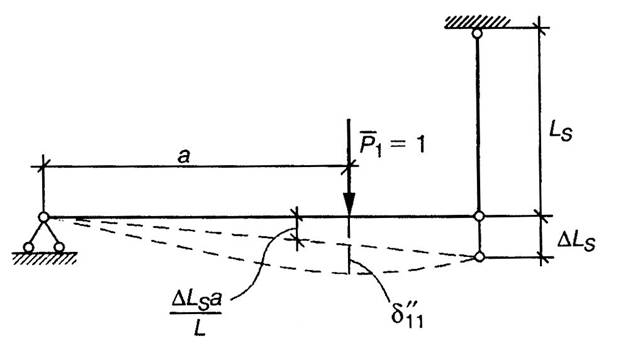
Рис.15.32

Введение упругой связи приводит к изменению собственной частоты системы с одной степенью свободы, изменению коэффициента нарастания колебаний и коэффициента динамичности. При сравнении двух случаев опирания все будет зависеть от того, в каком случае ближе будут частоты и , то есть ближе резонанс. Подрессоривание в случае колебаний не обязательно улучшает напряженно-деформированное состояние балки.

Пример 2.

Определить размеры поперечного сечения консольной балки с поперечным сечением, состоящим из двух швеллеров (рис. 15.33). На балке установлен электродвигатель, имеющий несбалансированную вращающуюся массу m. Произведение радиуса дисбаланса на массу кгм. Длина балки l=1 м. Число оборотов массы n=3000 об/мин. Вес двигателя P=2000 Н. Коэффициент усиления колебаний при резонансе =32. Допускаемое напряжение материала балки = 60 МПа.

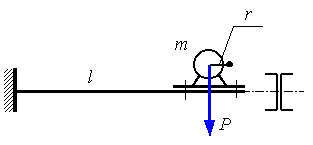
Рис. 15.33

Круговая частота возмущающей силы равна:

1/сек.

Частота собственных колебаний для консольной балки определяется по формуле:

.

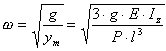Условие прочности имеет следующий вид:

,

Максимальные изгибающие моменты действуют в заделке и равны соответственно:

,

где амплитудное значение возмущающей (инерционной) силы равно .

Поскольку в условие прочности входят неизвестные моменты сопротивления и инерции, дальнейшие вычисления осуществляем методом последовательных приближений. Все расчеты для дорезонансной (первое приближение ) и зарезонансной (первое приближение ) областей сведены в таблицу 15.1.

Таблица 15.1.

	№ про- филя	, см4	Wz, см3	, 1/сек	b	, МПа	, МПа	, МПа	, МПа
0.8	-	5241	-	392.7	-	-	-	-	-
0.76	24	5800	484	413.08	2.368	10.195	24.14	4.132	28.276
0.89	22	4220	384	352.35	4.832	12.851	62.096	5.208	67.304
0.848	22a	4660	424	370.26	3.554	11.639	41.368	4.717	46.085
1.2	-	2330	-	261.8	-	-	-
1.187	18a	2380	264	264.6	2.43	18.692	45.454	7.576	53.030
1.427	16a	1646	206	220	0.962	23.955	23.055	9.708	32.763
5.875	6.5	97.2	30	53.47	0.030	164.5	4.908	66.06	71.57
4.329	8	179	44.8	72.6	0.056	110.15	6.208	44.643	50.851

Как видно из таблицы 15.1, условию прочности отвечают для дорезонансной области швеллер номера 22а, а для зарезонансной области – швеллер номер 8. При этом вес погонного метра швеллера номера 22а в 3,2 раза больше, чем для швеллера номера 8. Кроме этого для швеллера номер 8 по сравнению с номером 22а, при примерно одинаковых максимальных напряжениях цикла, значительно меньше амплитуда напряжений цикла, что имеет существенное значение для усталостной прочности.