Степень свободы колеблющейся системы

Колебания упругих систем принято различать по числу степеней свободы . Для упругой системы с геометрическими (голономными) связями под числом степеней свободы понимается число независимых координат, определяющих положение системы.

В случае кинематических (неголономных) связей число степеней свободы определяется числом независимых возможных перемещений.

На рис. 15.34 приведены примеры систем с сосредоточенными массами, степень свободы которых определяется по числу независимых перемещений , этих масс. В этих примерах мы пренебрегаем массой, распределённой в элементах самой системы.

Реальная система обладает бесконечным числом степеней свободы. Рассмотрим, например, балку на двух опорах (рис. 15.35). Ее можно разбить на любое число участков (в том числе и бесконечно малых ). Массу каждого участка можно сосредоточить в его середине. В зависимости от числа полученных сосредоточенных масс и количества их независимых перемещении мы можем легко подсчитать степень свободы системы. В пределе, когда число участков стремится к бесконечности, приходим к системе с бесконечным числом степеней свободы. В изображенном на рис. 15.35 случае n = 4.

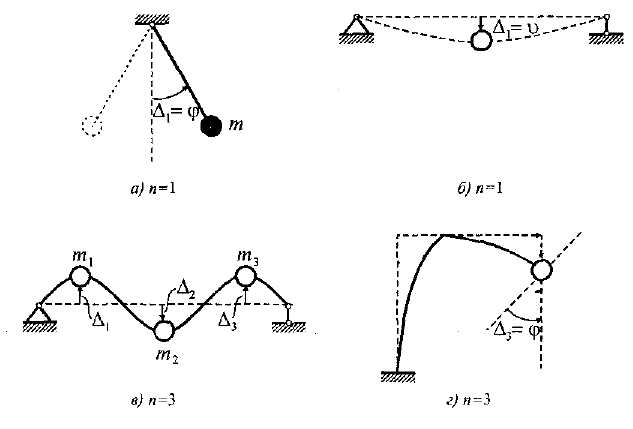
Рис. 15.34

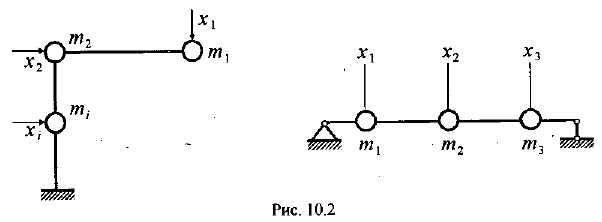
а) б)

Рис. 15.35

Таким образом, число степеней свободы системы определяется фактически выбором ее расчетной схемы т.е. степенью приближения, к реальной системе. Если, например, балка несет один сосредоточенный груз (рис. 15.34,а), масса которого значительно превышает массу самой балки, то в расчетной схеме системы естественно пренебречь массой балки и считать .

Канонические уравнения колебания упругих систем с конечным числом степеней свободы

Рассмотрим упругую систему, несущую несколько сосредоточенных масс . Пусть - силы, приложенные к этим грузам в направлении их смещений (рис. 15.36).

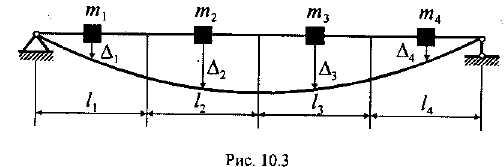
Рис. 15.36

Тогда перемещения этих грузов в направлении приложенных сил по закону Гука и принципу независимости действия сил определяются по формулам:

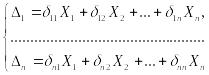(15.65)

или в сокращённой записи

(15.66)

Здесь - коэффициенты влияния, определяемые с помощью формулы Мора. Представим теперь, что наша система пришла в движение. Выясним природу сил в этом случае. На сосредоточенную массу может действовать внешняя сила , зависящая от времени и, согласно принципу Даламбера, - сила инерции . Следовательно,

(15.67)

Здесь точки над означают двукратное дифференцирование по времени. В свою очередь сила может состоять из постоянной (например, вес груза) и переменной частей:

(15.68)

Подставляя (15.67) в (15.66), получим форму записи уравнений движения упругих систем с конечным числом степеней свободы:

(15.69)

которые называются каноническими уравнениями колебаний упругих систем. При исследовании колебаний различают собственные (свободные) и вынужденные колебания. Под собственными колебаниями системы понимают такие, которые она совершает при отсутствии внешнего силового воздействия, т.е. предоставленная самой себе. В этом случае , и колебания поддерживаются только упругими силами. Под вынужденными колебаниями упругой системы понимают такие, которые происходят под действием возмущающих сил .