Приближенные методы определения низших частот собственных колебаний упругих систем

В большем числе случаев собственная распределенная масса упругих систем оказывается соизмеримой с присоединенными сосредоточенными массами. Поэтому сведение систем с бесконечным числом степеней свободы к системам с малым конечным числом степеней свободы оказывается не всегда приемлемым. В этих условиях предпочтительнее являются приближенные методы. Рассмотрим один из них – энергетический метод Релея.

Пусть имеется некоторая колебательная упругая система (рис.15.40, а) несущая собственный вес и несколько сосредоточенных масс . Наиболее опасной является первая форма колебаний, когда все массы колеблются в одной фазе (изогнутая ось 1 на рис. 15.40, б). В этом случае перемещения и напряжения в системе - наибольшие (мы отвлекаемся здесь от вопроса усталости материала, для которого существенными могут оказаться колебания с высокой собственной частотой).

Рассмотрим первую форму колебаний упругой системы. Если рассматривать колебания относительно статического положения равновесия системы, то закон движения любой точки упругой системы можно записать в виде

(15.112)

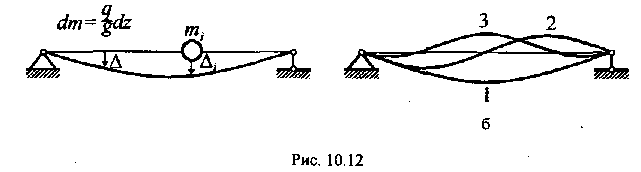
а) б)

Рис. 15.40

Перемещение массы будет:

(15.113)

На основании закона сохранения энергии для любых двух положений системы имеем:

(15.114)

где - потенциальная энергия упругой системы,

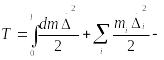(15.115)

кинетическая энергия системы.

Рассмотрим в качестве первого положения такое, при котором все массы проходят статическое положение равновесия. В этом положении и потенциальная энергия . Скорость

(15.116)

достигает максимального значения

(15.117)

Поэтому максимального значения достигает кинетическая энергия системы:

(15.118)

_{В качестве второго положения рассмотрим момент наибольшего отклонения системы от статического положения равновесия, когда кинетическая энергия} , а потенциальная достигает своего максимального значения _, равенство (15.114) можно теперь написать на основании вышеприведенных рассуждений в виде :

откуда получаем формулу Релея:

(15.119)

Для вычисления необходимо знать форму деформированного состояния упругой системы. Если задать ее приближенно, то этим самым мы как бы накладываем на систему дополнительные связи, т.е. делаем ее более жесткой. Вычисленная при этом частота со будет несколько завышенной по сравнению с точным значением. Если форму деформированного состояния угадать точно, то формула Релея даст точное значение низшей частоты колебаний упругой системы.

В случае изгиба балки для вычисления и имеем формулу:

(15.120)

В случае растяжения – сжатия стержня:

(15.121)

так как

(15.122)

Для случая кручения:

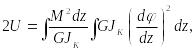(15.123)

так как

(15.124)

Понятие о приведенной массе

Рассмотрим упругую систему, например балку с распределенной массой (рис. 15.41, а). Поставим следующую задачу. Какую массу нужно приложить в некоторой точке такой же, но невесомой балки (рис. 15.41, б), чтобы низшие частоты колебаний исходной и упрощенной систем были одинаковы. Точку назовем точкой приведения массы системы, а массу - приведенной массой.

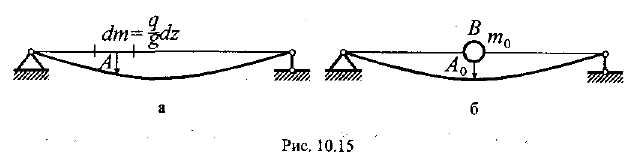
а) б)

Рис. 15.41

Если - коэффициент жесткости системы, то ее потенциальная энергия:

(15.125)

Подставляя (15.125) в формулу Релея (15.119), получим:

(15.126)

С другой стороны, для системы с одной степенью свободы имеем

(15.127)

Сравнивая (15.126) и (15.127), получим:

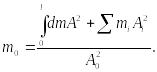(15.128)

Устойчивость вращающихся валов

Рассмотрим вал, вращающийся с угловой скоростью (рис. 15.42) и несущий сосредоточенные массы (диски).

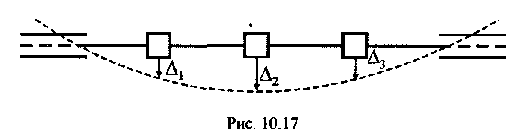
Рис. 15.42

Будем считать, что он идеально сбалансирован и при вращении сохраняет прямолинейную форму. Если скорость вращения невелика, то малые случайные воздействия приводят вал к изгибным колебаниям, которые быстро затухают. В этих условиях прямолинейная форма вала устойчива. При некоторых больших скоростях вращения прямолинейная форма вала перестает быть устойчивой. Получив при этих скоростях вращения прогиб от случайного воздействия, вал уже не возвращается к своему исходному, прямолинейному состоянию. Он теряет устойчивость своей прямолинейной формы. Скорость , при которой впервые вал не возвращается к своему исходному состоянию при действии случайного воздействия, называется критической угловой скоростью вращающегося вала.

Предположим, что при действии возмущающих сил в смысле Эйлера, вал отклонился от своей прямолинейной формы и остался в искривленном состоянии. Тогда при его вращательном движении возникают центробежные силы инерции , приложенные к сосредоточенным массам, в каждый момент движения уравновешиваются упругими силами. Поэтому перемещение массы , можно записать в виде:

Например, для системы с двумя сосредоточенными массами будем иметь:

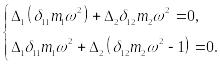(15.129)

Система (15.129) имеет отличные от нуля решения только в том случае, если определитель, составленный из ее коэффициентов, равен нулю:

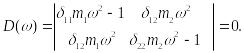(15.130)

В случае системы с степенями свободы получим выражение (15.84), т.е. критическая угловая скорость вращения в точности совпадает с частотой собственных колебаний вала как балки.

В частности, для системы с одной степенью свободы имеем:

(15.131)

Явлению неустойчивости вращающихся валов можно дать и несколько иное истолкование. Идеально сбалансированных валов не бывает и в них, с самого начала вращения, возникают центробежные силы инерции, которые растут с увеличением . Следовательно, растут и перемещения (рис. 15.43,а).

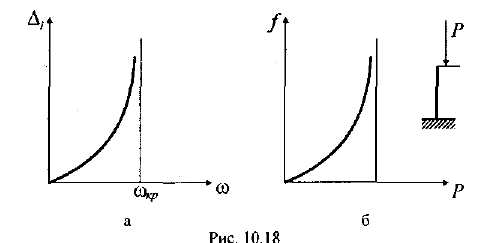
а) б)

Рис. 15.43

Здесь имеем явление, аналогичное таковому при эксцентричном сжатии гибкого стержня (рис. 15.43,б).

Колебания упругих систем при действии ударной нагрузки

Ударными, или импульсивными, нагрузками будем называть такие, которые действуют в течение весьма короткого промежутка времени. Если он значительно меньше периода собственных колебаний упругой системы, то за время действия ударной нагрузки не произойдет заметных перемещений ее точек или масс, но они приобретут некоторые конечные скорости

Расчет упругих систем на ударную нагрузку можно разбить на два этапа:

1. Определение скоростей, которые получат точки системы сразу после удара.

2. Изучение свободных колебаний системы после удара при заданном распределении начальных скоростей.

Ударное нагружение происходит тогда, когда по упругой системе ударяет масса, движущаяся с некоторой скоростью .

Будем рассматривать в дальнейшем только неупругий или неосвобождающий удар, когда ударяющее тело не отскакивает от упругой системы, по которой совершается удар, а «прилипает» к нему и совершает вместе с ним как единое целое колебательное движение. Будем считать также, что конфигурация системы при ее движении после удара считается заранее известной и неизменной.