13.6. Загальні поняття та означення теорії диференціальних рівнянь вищих порядків

Диференціальним рівнянням порядку (або -го порядку) називається рівняння вигляду , яке пов’язує незалежну змінну , невідому функцію та її похідні . Якщо це рівняння можна розв’язати відносно похідної , то маємо диференціальне рівняння -го порядку у вигляді: .

Розв’язком диференціального рівняння -го порядку на інтервалі називається раз диференційовна на цьому інтервалі функція , яка перетворює це рівняння у тотожність по на .

Задача Коші для диференціального рівняння -го порядку полягає у тому, щоб знайти розв’язок рівняння, який задовольняє початкові умови:

, де - задані дійсні числа (початкові значення).

Частинним розв’язком диференціального рівняння -го порядку називається функція , яка одержується із загального розв’язку фіксуванням деяких значень сталих.

Якщо загальний розв’язок диференціального рівняння знайдено у неявному вигляді, тобто у вигляді рівняння , то такий розв’язок називається загальним інтегралом диференціального рівняння. Рівність називають частинним інтегралом диференціального рівняння.

Теорема Коші (достатні умови існування та єдиності розв’язку задачі Коші). Якщо у диференціальному рівнянні -го порядку функція неперервна та має неперервні частинні похідні по змінним в деякій області , що містить точку початкових значень , то існує єдиний розв’язок цього рівняння , який задовольняє початкові умови .

Зауважимо, що на відміну від випадку диференціального рівняння першого порядку, через кожну точку площини буде проходити не одна, а безліч інтегральних кривих диференціального рівняння -го порядку. Дійсно, нехай задано диференціального рівняння другого порядку з початковими умовами . Зафіксуємо , тоді через цю точку буде проходити єдина інтегральна крива з кутом нахилу дотичної до осі абсцис , причому . Якщо змінювати при незмінних , то одержимо безліч інтегральних кривих з різними кутами нахилу, що проходять через задану точку.

13.7.Диференціальні рівняння вищих порядків, що допускають зниження порядку

1. Рівняння вигляду .

Загальний розв’язок цього рівняння знаходиться -кратним інтегруванням початкового рівняння. Враховуючи, що , маємо:

;

;

;

…….. ……. ……;

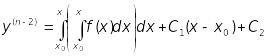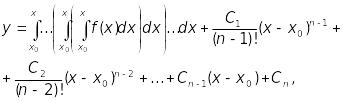(13.29)

де - довільне значення змінної з області існування розв’язку рівняння, - довільні сталі. Остання рівність визначає загальний розв’язок рівняння. Частинний розв’язок, що задовольняє умови , можна одержати з (13.29), поклавши .

2. Рівняння вигляду , що не містить шуканої функції ( ).

Порядок такого рівняння можна понизити, якщо ввести нову функцію , тоді . Початкове рівняння зводиться до рівняння порядку відносно невідомої функції : .

3. Рівняння вигляду , що не містить незалежної змінної.

Такі рівняння допускають пониження порядку на одиницю, якщо покласти , де - нова залежна змінна. Дійсно, тоді

; ,

і так далі, а задане рівняння зводиться до диференціального рівняння порядку .