4. Рівняння вигляду , яке є однорідним відносно .

Рівняння даного типу допускають пониження порядку на одиницю при заміні невідомої функції на нову функцію .

Приклад 15. Розв’язати задачу Коші .

Запропоноване рівняння розв’язується шляхом двократного інтегрування.

Якщо , то маємо:

;

.

Отже, загальний розв’язок рівняння задається співвідношенням

.

Скористуємось початковими умовами для знаходження розв’язку задачі Коші: , звідки та .

Якщо , то задане рівняння набуває вигляду , звідки маємо . Враховуючи початкові умови , одержимо .

Приклад 16. Розв’язати диференціальне рівняння .

Рівняння не містить шуканої функції , тому введемо нову функцію , після чого рівняння перетвориться у наступне або .

Одержане рівняння є однорідним першого порядку. Покладаючи , матимемо рівняння або .

Інтегруючи останнє рівняння, знаходимо

; ; .

Повертаючись до змінної одержимо диференціальне рівняння першого порядку , звідки

.

Приклад 17. Розв’язати диференціальне рівняння .

Рівняння не містить незалежної змінної , тому зробимо заміну , де - нова залежна змінна, після чого рівняння перетвориться у наступне або , звідки

; ; .

Враховуючи , маємо:

; ; .

Приклад 18. Розв’язати диференціальне рівняння .

Рівняння є однорідним відносно , тому поділимо його на , та одержимо рівняння у вигляді .

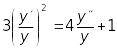Зробимо заміну невідомої функції: ; 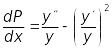або , тоді матимемо:

; ; ;

; ; ;

; .

Зауважимо, що є частинним розв’язком рівняння.

13.8. Лінійні диференціальні рівняння другого порядку

Диференціальне рівняння другого порядку називається лінійним, якщо невідома функція та її похідні входять в це рівняння в першій степені, тобто це рівняння вигляду , де - відомі функції, .

Надалі будемо вважати, що функції неперервні на та . Якщо , то лінійне рівняння називається неоднорідним, а якщо , то – однорідним.

Розглянемо лінійне однорідне диференціальне рівняння

(13.30)

та встановимо його властивості.

Лема 1. Якщо - частинні розв’язки рівняння (13.30), то їхня сума є також розв’язком рівняння (13.30).

Дійсно, в силу припущення леми, - частинні розв’язки рівняння (13.30), тому мають місце рівності:

,

звідки , отже, є розв’язком рівняння (13.30).

Лема 2. Якщо - частинний розв’язок рівняння (13.30), - довільна стала, то їхній добуток є також розв’язком рівняння (13.30).

Лема 2 доводиться аналогічно доведенню леми 1.

Два частинні розв’язки рівняння (13.30), називаються лінійно незалежними на відрізку , якщо їх відношення на цьому відрізку не є сталим, тобто . Якщо , то називаються лінійно залежними на , в цьому випадку .

Якщо - деякі функції, то визначник

(13.31)

називається визначником Вронського (вронскіаном) даних функцій.

Теорема 1. Якщо лінійно залежні на , то їхній вронскіан на цьому відрізку дорівнює нулю.

Нехай , , тоді та .

Теорема 2. Якщо вронскіан , складений для розв’язків рівняння (13.30), не дорівнює нулю при деякому значенні незалежної змінної на відрізку , де коефіцієнти рівняння (13.30) неперервні, то він не обертається в нуль при жодному значенні на цьому відрізку.

Нехай - розв’язки рівняння (13.30), тому мають місце рівності:

.

Помножимо друге рівняння на , перше рівняння – на та віднімемо результати:

.

Зауважимо, що , тоді маємо диференціальне рівняння першого порядку відносно вронскіана:

.

Знайдемо його розв’язок, який задовольняє початкову умову . Якщо , то маємо:

; ; .

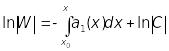Враховуючи початкову умову одержимо та

. (13.32)

Рівність (13.32) називається формулою Ліувіля - Остроградського. За умовою теореми , тому з (13.32) випливає, що для будь-якого .

Теорема 3. Якщо розв’язки рівняння (13.30) лінійно незалежні на , то їхній вронскіан не обертається в нуль при жодному значенні з .

Доведення теореми проводиться від супротивного.

Сукупність двох розв’язків рівняння (13.30), визначених і лінійно незалежних на , називається фундаментальною системою розв’язків.

Теорема 4. Якщо - фундаментальна система розв’язків рівняння (13.30), то

, (13.33)

де - довільні сталі, є його загальним розв’язком.

Дійсно, з властивостей розв’язків рівняння (13.30) випливає, що (13.33) є розв’язком рівняння (13.30). Доведемо, що для будь-яких початкових умов можна підібрати значення сталих так, щоб відповідний частинний розв’язок задовольняв початкові умови. Підставимо задані початкові умови в (33):

.

З одержаної системи можна визначити відповідні , бо визначник системи не дорівнює нулю в силу лінійної незалежності частинних розв’язків. Отже, частинний розв’язок, який одержується з сім’ї (13.33) при відповідних (знайдених) , задовольняє початкові умови.

Слід зауважити, що не існує загальних методів знаходження в завершеному вигляді загального розв’язку рівняння (13.30) із змінними коефіцієнтами. При практичних діях може бути корисною наступна теорема.

Теорема 5. Якщо відомий один частинний розв’язок рівняння (13.30), то знаходження загального розв’язку зводиться до інтегрування функцій.

Нехай - частинний розв’язок рівняння (13.30). Знайдемо частинний розв’язок , лінійно незалежний з на .

Скористаємося формулою Ліувіля – Остроградського

;

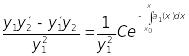
або

,

звідки

.

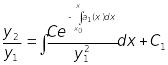В силу того, що ми шукаємо частинний розв’язок, покладемо , тоді

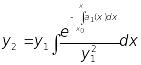. (13.34)

Очевидно, що є лінійно незалежними на , бо . Отже, загальний розв’язок рівняння (30) має вигляд

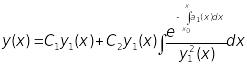. (13.35)

Розглянемо лінійне неоднорідне диференціальне рівняння

(13.36)

Розв’язок (13.36) будемо шукати методом варіації довільних сталих у вигляді:

,

де - фундаментальна система розв’язків рівняння (13.30), - невідомі функції. Обчислимо першу похідну:

.

Підбираємо шукані функції так, щоб виконувалась рівність: , тоді

.

Підставимо в (35), одержимо:

Враховуючи те, що - розв’язки рівняння (13.30), з останнього співвідношення маємо систему рівнянь для знаходження :

визначник якої в силу лінійної незалежності .

Якщо позначити розв’язки системи , то , де - довільні сталі.

Отже, загальний розв’язок лінійного неоднорідного диференціального рівняння другого порядку має вигляд:

, (13.37)

де перші два доданки є загальним розв’язком лінійного однорідного, а два останні – частинним розв’язком лінійного неоднорідного диференціального рівняння.

Теорема 6. Загальний розв’язок лінійного неоднорідного диференціального рівняння другого порядку дорівнює сумі загального розв’язку лінійного однорідного диференціального рівняння другого порядку та частинного розв’язку лінійного неоднорідного диференціального рівняння другого порядку.

Ця теорема доводиться аналогічно доведенню теореми 4.

Теорема 7. Нехай задано лінійне неоднорідне диференціальне рівняння другого порядку вигляду та є частинним розв’язком рівняння , а - частинним розв’язком рівняння , тоді є частинним розв’язком заданого рівняння.

Доведення теореми випливає з лінійності похідних.

Сформульована теорема називається теоремою накладання розв’язків (принцип накладання).

Приклад 19. Розв’язати задачу Коші .

Запропоноване рівняння є лінійним неоднорідним диференціальним рівнянням другого порядку. Розв’яжемо, спочатку, однорідне рівняння:

.

Маємо:

, , , .

Розв’язок неоднорідного рівняння будемо шукати методом варіації довільних сталих у вигляді: .

Складемо систему для знаходження :

звідки ; .

Тоді загальний розв’язок лінійного неоднорідного диференціального рівняння другого порядку набуде вигляду або .

Для розв’язання задачі Коші знаходимо: , тоді

; .

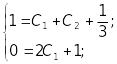
Приклад 20. Розв’язати диференціальне рівняння , якщо відомий частинний розв’язок однорідного рівняння.

Для знаходження частинного розв’язку однорідного рівняння, лінійно незалежного з застосуємо формулу (34), тоді

.

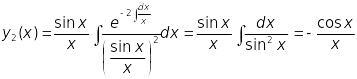Загальний розв’язок однорідного рівняння має вигляд:

.

Розв’язок неоднорідного рівняння шукаємо у вигляді:

.

Складемо систему для знаходження :

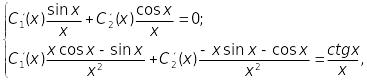
вронскіан якої дорівнює . Тому

звідки одержимо загальний розв’язок неоднорідного рівняння:

.