
- •Лекція 16: економічна динаміка та її моделювання: диференціальні та різницеві рівняння
- •13.1. Звичайні диференціальні рівняння. Загальні поняття та означення теорії диференціальних рівнянь першого порядку
- •13.2.Рівняння з відокремлюваними змінними
- •13.3.Однорідні диференціальні рівняння
- •13.4Лінійні диференціальні рівняння
- •13.5.Рівняння у повних диференціалах
- •13.6. Загальні поняття та означення теорії диференціальних рівнянь вищих порядків
- •13.7.Диференціальні рівняння вищих порядків, що допускають зниження порядку
- •Рівняння вигляду , що не містить шуканої функції ( ).
- •Рівняння вигляду , що не містить незалежної змінної.
- •Рівняння вигляду , яке є однорідним відносно .
- •13.8. Лінійні диференціальні рівняння другого порядку
- •13.9. Лінійні диференціальні рівняння вищих порядків
- •13.10. Лінійні диференціальні рівняння вищих порядків зі сталими коефіцієнтами
13.5.Рівняння у повних диференціалах
Диференціальне рівняння вигляду
, (13.19)
називається
рівнянням
у повних диференціалах,
якщо
![]() - неперервні функції, причому
- неперервні функції, причому
![]() .
(13.20)
.
(13.20)
Назва
рівняння пояснюється тим, що при виконанні
умови (13.20) ліва частина рівняння (13.19) є
повним диференціалом, тобто існує така
диференційовна функція
![]() ,
що має місце рівність
,
що має місце рівність
![]() ,
(13.21)
,
(13.21)
Доведемо,
що (13.20) є необхідною і достатньою умовою
(13.21). Дійсно, нехай виконується (13.21),
тоді
![]() ,
звідки
,
звідки
![]() .
В силу неперервності частинних похідних
маємо
.
В силу неперервності частинних похідних
маємо
![]() ,
тому
.
,
тому
.
Нехай виконується умова (13.20). Побудуємо деяку диференційовну функцію таку, щоб мало місце (13.21) або .
Із першої рівності маємо:
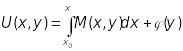 ,
(13.22)
,
(13.22)
де
![]() - абсциса будь-якої точки з області
існування розв’язку рівняння. При
інтегруванні по
змінна
вважається
параметром, тому і довільна стала
інтегрування має залежати від
.
Підберемо функцію
- абсциса будь-якої точки з області
існування розв’язку рівняння. При
інтегруванні по
змінна
вважається
параметром, тому і довільна стала
інтегрування має залежати від
.
Підберемо функцію
![]() так, щоб виконувалось
так, щоб виконувалось
![]() .
Для цього диференціюємо (13.22) по
:
.
Для цього диференціюємо (13.22) по
:
 ,
,
тоді з врахуванням (20)
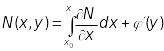 ;
;
![]() ;
;
![]() ;
;
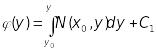 .
.
Отже, шукана функція матиме вигляд
 ,
(13.23)
,
(13.23)
де
- деяка точка з області існування
розв’язку
диференціального рівняння. Нагадаємо,
що (23) – це функція, диференціал якої
дорівнює лівій частині рівняння (19),
тому загальний інтеграл цього рівняння
має вигляд
![]() або
або
 .
(13.24)
.
(13.24)
Зауважимо, що при практичному використанні формул (13.22), (13.23), (13.24) можна обчислювати невизначені інтеграли замість визначених.
Якщо
умова (13.20) не виконується, то інколи
вдається підібрати таку функцію
![]() ,
після множення на яку всіх частин
рівняння (13.19) ліва частина цього рівняння
стає повним диференціалом. Функція
називається інтегрувальним
множником
рівняння (13.19).
,
після множення на яку всіх частин
рівняння (13.19) ліва частина цього рівняння
стає повним диференціалом. Функція
називається інтегрувальним
множником
рівняння (13.19).
Помножимо (13.19) на :
![]() .
.
Це
рівняння буде рівнянням у повних
диференціалах, якщо
![]() ,
тобто
,
тобто
![]() ;
;
![]() ;
;
![]() .
(13.25)
.
(13.25)
Рівняння (13.25) є диференціальним рівнянням у частинних похідних відносно невідомої функції . Доведено, що при певних умовах це рівняння має безліч розв’язків, тобто існує, але у загальному випадку задача (13.25) складніша, ніж задача (13.19).
Розглянемо
частинні випадки. Нехай
![]() ,
тоді
,
тоді
![]() ,
а співвідношення (13.25) набуде вигляду
,
а співвідношення (13.25) набуде вигляду
![]() .
(13.26)
.
(13.26)
Якщо права частина рівності (13.26) не залежить від змінної , то
![]() .
(13.27)
.
(13.27)
Аналогічно,
якщо
![]() ,
то інтегрувальний множник обчислюється
за формулою:
,
то інтегрувальний множник обчислюється
за формулою:
![]() .
(13.28)
.
(13.28)
Приклад
12.
Розв’язати
диференціальне рівняння
![]() .
.
Дане рівняння є рівнянням у повних диференціалах, бо виконується умова (20), дійсно
![]() .
.
Застосуємо
формулу (22) для знаходження функції
![]() :
:
![]() ,
,
звідки в силу
![]() ;
;
![]() ;
;
![]() .
.
Отже,
![]() ,
тому загальним інтегралом рівняння є
,
тому загальним інтегралом рівняння є
![]() .
.
Приклад
13.
Розв’язати
диференціальне рівняння
![]() .
.
Для даного рівняння не виконується умова (13.20), бо
![]() .
.
Складемо вираз, що є лівою частиною співвідношення (13.26):
![]() ,
,
звідки
маємо
![]() ;
;
![]() .
.
Вибираємо
і одержуємо шуканий інтегрувальний
множник
![]() .
Помножимо початкове рівняння на
:
.
Помножимо початкове рівняння на
:
![]() .
.
Для цього рівняння умова повного диференціала (13.20) справджується, тому
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отже,
загальний інтеграл рівняння
![]() .
.
Приклад
14.
Розв’язати
диференціальне рівняння
![]() .
.
Для даного рівняння не виконується умова (13.20), бо

Шукаємо інтегрувальний множник рівняння, припускаючи що :
![]() ,
,
звідки
маємо
![]() ;
;
![]() ;
;
![]() .
Вибираємо
та множимо початкове рівняння на
.
Вибираємо
та множимо початкове рівняння на
![]() :
:
![]() .
.
Легко перевірити, що останнє рівняння є рівнянням в повних диференціалах, тому маємо
 .
.
Знайдемо похідну по від одержаної функції:
![]() .
.
Скориставшись
рівністю
![]() ,
одержимо
,
одержимо
![]() ,
,
звідки
![]() ,
тобто
,
тобто
![]() .
Остаточно маємо загальний інтеграл
рівняння:
.
Остаточно маємо загальний інтеграл
рівняння:
![]() .
.
