13.4Лінійні диференціальні рівняння

Диференціальне рівняння вигляду

, (13.12)

де - відомі неперервні функції, називається лінійним рівнянням. Якщо , то (13.12) називається лінійним неоднорідним, а якщо , то – лінійним однорідним.

Інтегрування лінійних рівнянь здійснюється методом Лагранжа (варіації довільної сталої) або методом Бернуллі.

За методом Лагранжа спочатку розв’язують лінійне однорідне рівняння

, (13.13)

яке є рівнянням з відокремлюваними змінними, тому при мають

; ;

. (13.14)

Рівняння (13.14) є загальним розв’язком (13.13), причому частинний розв’язок міститься у ньому при .

Загальний розв’язок лінійного неоднорідного рівняння шукають у вигляді

, (13.15)

де - невідома диференційовна функція. Диференціюючи (13.15), мають:

,

тоді (13.12) набуде вигляду:

,

звідки ; .

Отже, загальний розв’язок лінійного неоднорідного рівняння має вигляд:

, (13.16)

де перший доданок є загальним розв’язком лінійного однорідного рівняння, а другий – частинним розв’язком лінійного неоднорідного рівняння.

За методом Бернуллі шукають загальний розв’язок лінійного неоднорідного рівняння у вигляді , де - невідомі диференційовні функції. Враховуючи співвідношення , рівняння (12) перетворюється у наступне: , звідки

. (13.17)

Зауважимо, що одну з функцій можна обирати довільним чином, тому шукають як розв’язок рівняння з відокремлюваними змінними , звідки . Обирають значення довільної сталої та повертаються до рівняння (13.17), підставивши в нього знайдену функцію , тоді , звідки . Остаточно, враховуючи , одержують загальний розв’язок, що співпадає з (13.16).

Диференціальне рівняння вигляду

, (13.18)

де - відомі неперервні функції, називається рівнянням Бернуллі. Це рівняння перетворюється і лінійне неоднорідне, якщо зробити заміну невідомої функції , тоді (18) набуде вигляду: . Зауважимо, що при інтегруванні рівняння Бернуллі не обов’язково виконувати запропоновану заміну, а можна зразу застосовувати методи Лагранжа або Бернуллі.

Приклад 8. Розв’язати диференціальне рівняння .

Рівняння є лінійним неоднорідним, застосуємо метод Лагранжа. Інтегруємо відповідне однорідне рівняння:

; ; ; .

Шукаємо розв’язок неоднорідного рівняння у вигляді

, тоді .

Підставимо вказані та у неоднорідне рівняння

;

;

.

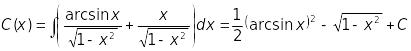Отже, загальний розв’язок заданого рівняння має вигляд

.

Приклад 9. Розв’язати диференціальне рівняння .

Запропоноване рівняння стане лінійним, якщо поміняти місцями шукану функцію та незалежну змінну, тобто будемо вважати , тоді рівняння можна переписати у диференціалах , звідки одержимо лінійне рівняння відносно невідомої функції : .

Розв’яжемо це рівняння методом Бернуллі. Зробимо заміну , тоді

; ; .

Шукаємо невідому функцію як розв’язок лінійного однорідного рівняння: ; ; ; .

Вибираємо , тоді та , звідки . Тоді, маємо

.

Приклад 10. Розв’язати задачу Коші .

Маємо рівняння Бернуллі (18) з . Зробимо заміну , тоді . Одержане рівняння є лінійним неоднорідним відносно невідомої функції . Застосуємо метод варіації довільної сталої:

; ; .

Нехай , тоді , звідки ;

; ; .

Розв’яжемо задачу Коші: ,тому .

Приклад 11. Розв’язати диференціальне рівняння .

Будемо вважати , тоді рівняння перетвориться у наступне , яке є рівнянням Бернуллі з . Застосуємо метод Лагранжа: ; ; ; . Нехай , тоді

; ;

; .

Остаточно, загальним розв’язком рівняння є .