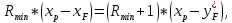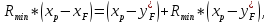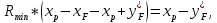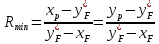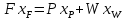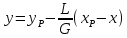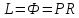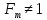- •Первые вопросы
- •Вопрос 1 Вывестии дифференциальное уравнение конвективной диффузии. Рассмотреть частный случай диффузии в неподвижной среде.
- •2. Первый закон Фика. Вывод дифференциального уравнения конвективной диффузии.
- •3. Получить диффузионные критерии подобия. Определяемый и определяющие критерии. Физический смысл массообменных критериев подобия.
- •4. Получить уравнение аддитивности диффузионных сопротивлений. Сформулировать допущения при выводе.
- •5. Вывести соотношение между коэффициентами массопередачи и массоотдачи. Из каких уравнений получают коэффициенты массоотдачи?
- •Вопрос №8. Вывод уравнения для расчета средней движущей силы массопередачи.
- •1)Через основное уравнение массопередачи.
- •2) Через число теоретических тарелок.
- •3) Метод кинетической (псевдоравновесной) линии.
- •Вопрос 14. Материальный баланс процесса простой перегонки. Расчет количества кубового остатка, количества и среднего состава дистиллята.
- •16. Вывести уравнение рабочей линии для укрепляющей части ректификационной колонны. Описать, как строят рабочие линии на диаграмме y-X, сформулировав необходимые допущения.
- •Выбор рабочего флегмового числа
- •21. Вывести уравнение теплового баланса ректификационной колонны непрерывного действия. Как определяется расход греющего пара в кипятильнике?
Вопрос 14. Материальный баланс процесса простой перегонки. Расчет количества кубового остатка, количества и среднего состава дистиллята.
Простая перегонка заключается в постепенном испарении жидкости и конденсации образующихся паров. Рассмотрим периодически действующую перегонку. В куб залита жидкая смесь. Составим уравнение материального баланса.
Пусть в момент времени τ в кубе L кг смеси, х – концентрация НК в смеси, Lх – количество НК в смеси.
За время dτ испарится dL кг смеси и концентрация уменьшится на dx. При этом образуется dL кг пара, равновесного с жидкостью и имеющего концентрацию у*; dLy* – количество НК в паре. В кубе останется остаток (L – dL) кг с концентрацией (х – dx).
Тогда уравнение материального баланса по НК:
Lx = (L–dL)(x–dx)+dLy*;
Раскроем скобки: Lх = Lх– dLх– Ldx+ dLdx+ dLy*,
после
сокращения получим: dL(y*–х) = Ldx,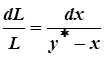
разделим переменные:
Это дифференциальное уравнение проинтегрируем от L = F (количество исходной смеси) до L = W (количество остатка) и по х от хF до хW (хF – концентрация НК в исходной смеси; хW –концентрация в остатке).
Тогда: ∫ dL/L = ∫ dx/(y* – х); ln(F/W) = ∫ dx/(y* – х) – W хW хW
– уравнение простой перегонки.
Вид функции у* = f(x) определяется формой кривой равновесия и не может быть установлен аналитически. Поэтому правую часть интегрируют графически.
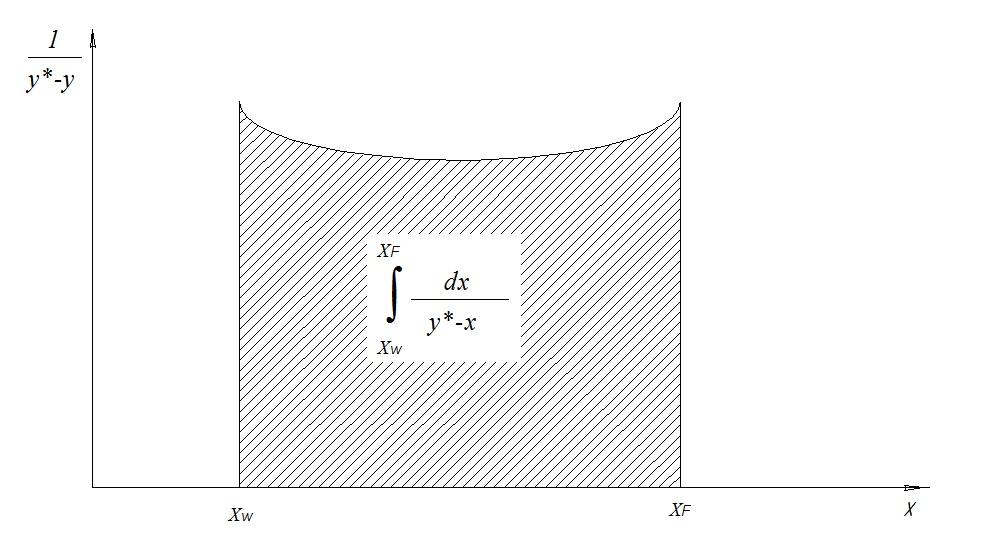
Из уравнения можно получить W, зная F и хF, хW. Средний состав дистиллята хр можно определить из уравнения материального баланса по НК:
FхF = WхW + (F – W) (хр)ср. , где хр = (FхF – WхW)/(F – W).
Простая перегонка применяется для смесей, компоненты которых сильно различаются по летучести, простая перегонка – это довольно грубое предварительное разделение смесей.
Вопрос № 15. Вывести уравнения рабочих линий ректификационной колонны непрерывного действия.

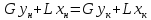
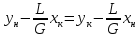
Делаем подстановку в 1 уравнение:
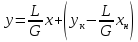
Укрепляющая часть колонны. Количество жидкости (флегмы), стекающей по этой части колонны
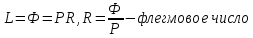
Количество паров, поднимающихся по колонне

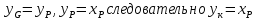
В том же сечение колонны состав жидкости (флегмы) , поступающей из дефлегматора,
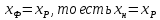
Подставляя значения L, G, yк, xк , получаем:
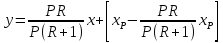
Откуда
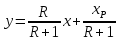 -
эта зависимость является уравнением
рабочей линии укрепляющей части колонны.
-
эта зависимость является уравнением
рабочей линии укрепляющей части колонны.
Количество жидкости, стекающей по исчерпывающей части колонны, составит:
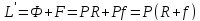
Количество пара, проходящего через нижнюю часть колонны, равно количеству пара, поднимающегося по верхней (укрепляющей) ее части. Следовательно:
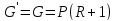
Для низа колонны состав удаляющейся жидкости (остатка) x’к=xw и, согласно допущению, состав поступающего сюда из кипятильника пара y’н= yw = xw . Подставив значения L’, G’, x’к , y’н в первое уравнение, получим:
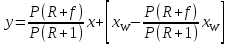
После приведения к общему знаменателю и сокращения подобных членов находим:
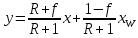 эта
зависимость является уравнением рабочей
линии исчерпывающей части колонны.
эта
зависимость является уравнением рабочей
линии исчерпывающей части колонны.
16. Вывести уравнение рабочей линии для укрепляющей части ректификационной колонны. Описать, как строят рабочие линии на диаграмме y-X, сформулировав необходимые допущения.
Упрощающие
допущения графического метода анализа
работы и расчета ректификационной
колонны.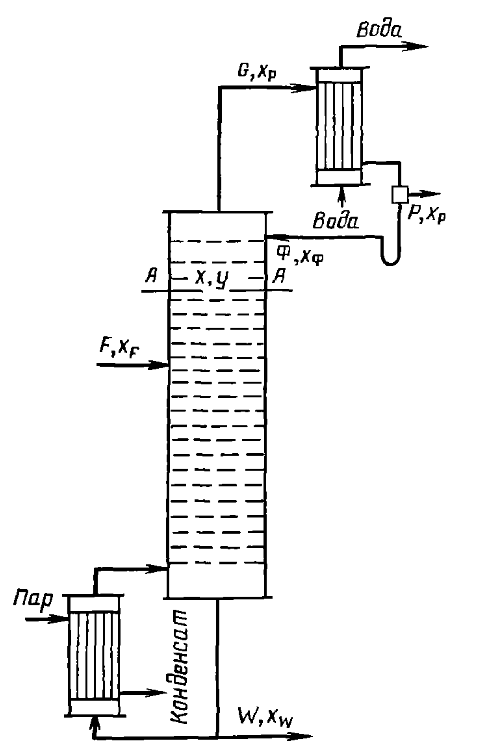
-
Молярные теплоты испарения компонентов при одной и той же температуре приблизительно одинаковы (правило Трутона), поэтому каждый киломоль пара при конденсации испаряет 1 кмоль жидкости. Следовательно количество поднимающихся паров (в киломолях) в любом сечении колонны одинаково;
-
В дефлегматоре не происходит изменения состава пара. Если весь пар конденсируется в дефлегматоре, то это положение полностью соответствует реальным условиям. Следовательно, состав пара, уходящего из ректификационной колонны, равен составу дистиллята, т.е.
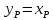 ;
; -
При испарении жидкости в кипятильнике не происходит изменения ее состава. Следовательно, состав пара, образующегося в кипятильнике, соответствует составу кубового остатка, т.е.
 ;
; -
Теплоты смешения компонентов разделяемой смеси равны 0.
Также, при этом перед подачей в колонну смесь подогревают до температуры кипения жидкости в том сечении колонны, в которое она поступает.
Вывод уравнения рабочей линии для укрепляющей части ректификационной колонны
Обозначения:
-
F, xF - поток (кмоль/с) и концентрация (молярные доли) НК исходной смеси;
-
P, xP - поток и концентрация НК дистиллята;
-
W,xW - поток и концентрация НК кубового остатка;
-
Ф,xФ – поток и концентрация НК флегмы;
-
G – количество пара (кмоль/с), выходящего из колонны.
Материальный баланс колонны по всему потоку:
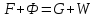 ;
при
;
при
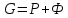 получаем
получаем

Материальный баланс по низкокипящему компоненту:
Для укрепляющей части колонны возьмем произвольное сечение А-А (см. рис), которому соответствуют текущие концентрации x и y, и составим материальный баланс по НК для верха этой колонны:

откуда
где
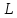 –
количество флегмы, стекающей в верхней
части колонны.
–
количество флегмы, стекающей в верхней
части колонны.
Количество поднимающихся по колонне паров:
С
учетом
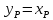 (см допущение 2), поставляем ур-я (3) и (4)
в ур-е (2). Получаем:
(см допущение 2), поставляем ур-я (3) и (4)
в ур-е (2). Получаем:
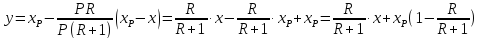
Таким образом, уравнение рабочей линии укрепляющей части колонны:
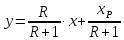
Порядок
построения рабочих линий ректификационной
колонны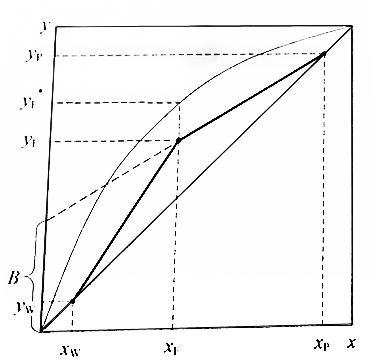
-
Откладываем на горизонтальной оси значения
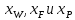 ;
; -
Строим на диагонали точки
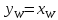 и
и
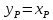 ;
; -
Проводим вертикаль при
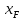 до значения
до значения
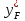 ;
; -
Откладываем на вертикальной оси отрезок
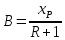 ;
; -
Соединяем точку на вертикальной оси, полученную по отрезку В, и точку на диагонали
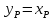 пунктирной линией;
пунктирной линией; -
На пересечении пунктирной линии и вертикали (при
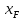 )
получаем точку пересечения рабочих
линий (точку питания);
)
получаем точку пересечения рабочих
линий (точку питания); -
Соединяя точку пересечения рабочих линий с точкой
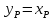 ,
получаем рабочую линию верхней части
колонны;
,
получаем рабочую линию верхней части
колонны; -
Соединяя точку пересечения рабочих линий с точкой
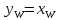 ,
получаем рабочую линию нижней части
колонны.
,
получаем рабочую линию нижней части
колонны.
17. Вывести уравнения рабочих линий для ретификационной колонны непрерывного действия при постоянстве расходов фаз (с необходимыми пояснениями и допущениями). Как зависит положение этих линий на диаграмме у-х от флегмового числа?
Предварительно принимаются следующие основные допущения, мало искажающие действительный процесс, но существенно упрощающие его анализ и расчет:
1. Молярные теплоты испарения компонентов при одной и той же температуре приблизительно одинаковы (правило Трутона), поэтому каждый киломоль пара при конденсации испаряет 1 кмоль жидкости. Следовательно, количество поднимающихся паров (в киломолях) в любом сечении колонны одинаково.
2. В дефлегматоре не происходит изменения состава пара. Если весь пар конденсируется в дефлегматоре, то это положение полностью соответствует реальным условиям. Следовательно, состав пара, уходящего из ректификационной колонны, равен составу дистиллята, т.е. yD = xD.
3. При испарении жидкости в кипятильнике не происходит изменения ее состава. Следовательно, состав пара, образующегося в кипятильнике, соответствует составу кубового остатка, т.е. yW = xW.
4. Теплоты смешения компонентов разделяемой смеси равны нулю.
При этом предполагается, что перед подачей в колонну смесь подогревают до температуры кипения жидкости в том сечении колонны, в которое она поступает.
Расчетная схема установки представлена на рис. 3.15.
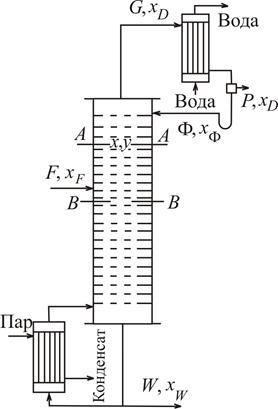
Рис. 3.15. К выводу уравнения материального баланса
Введены следующие обозначения (рис. 3.15):
F, xF – поток (кмоль/с) и концентрация (молярные доли) НК исходной смеси;
P, xD – поток и концентрация НК дистиллята;
W, xW – поток и концентрация НК кубового остатка;
Ф, xФ – поток и концентрация НК флегмы;
G – количество пара (кмоль/с), выходящего из колонны.
Тогда материальный баланс колонны по всему потоку
![]()
но G = P + Ф, и поэтому
F = P + W. (3.8)
Материальный баланс по низкокипящему компоненту
![]() (3.9)
(3.9)
Уравнения рабочих линий. Поскольку условия работы укрепляющей и исчерпывающей частей ректификационной колонны различны, то рассмотрим материальные балансы для них отдельно.
Для укрепляющей части колонны возьмем произвольное сечение А – А (рис. 3.15), которому соответствуют текущие концентрации x и y, и составим материальный баланс по НК для верха этой части колонны:
![]()
откуда
![]() (3.10)
(3.10)
где L – количество флегмы, стекающей в верхней части колонны.
Причем
![]() (3.11)
(3.11)
где R –
флегмовое число, равное отношению
количества флегмы к количеству
отбираемого из колонны дистиллята: ![]()
Количество поднимающихся по колонне паров
![]() (3.12)
(3.12)
Так как по принятому допущению yD = xD, то уравнение (3.10) при подстановке в него соответствующих значений L и G принимает вид
|
|
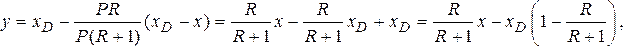
откуда получаем уравнение рабочей линии укрепляющей части колонны:
![]() (3.13)
(3.13)
При x = xD y = xD, т.е. рабочая линия укрепляющей части колонны пересекает диагональ с абсциссой xD, что и следовало ожидать, учитывая второе допущение.
Обозначим ![]() ,
а
,
а ![]() .
Тогда уравнение (3.13) примет вид соотношения
.
Тогда уравнение (3.13) примет вид соотношения
![]()
которое является уравнением прямой линии. В нем А – тангенс угла наклона a рабочей линии к оси абсцисс, а В – отрезок, отсекаемый рабочей линией на оси ординат (рис. 3.16, а).
При выводе уравнений рабочей линии исчерпывающей части колонны следует учитывать, что количество орошения этой части колонны увеличивается на величину расхода F исходной смеси. Рассмотрим материальный баланс для низа исчерпывающей части колонны – ниже произвольного сечения В – В (рис. 3.15); текущие концентрации НК в фазах x и y .
Обозначим
количества поднимающегося по нижней
части колонны пара ![]() ,
а стекающей флегмы –
,
а стекающей флегмы – ![]() .
Тогда
.
Тогда
![]()
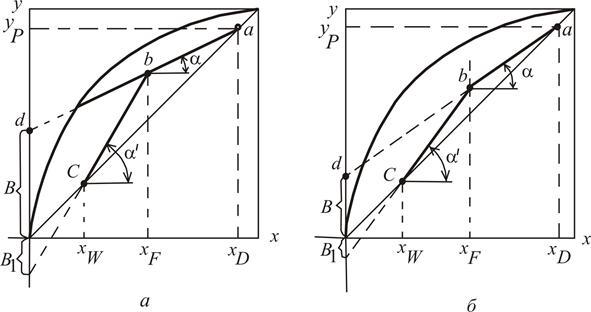
Рис. 3.16. К выводу уравнений рабочих линий верхней (а) и нижней (б) частей ректификационной колонны
Если
обозначить через ![]() то
то ![]() Количество
стекающей по нижней части колонны
флегмы
Количество
стекающей по нижней части колонны
флегмы ![]() Количество
поднимающегося по колонне пара не
меняется, т.е.
Количество
поднимающегося по колонне пара не
меняется, т.е.
![]()
откуда
![]()
Тогда с учетом того, что yW = xW, получим
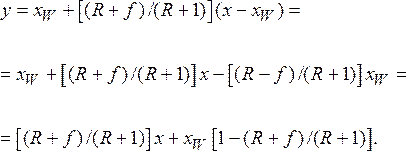
После соответствующих преобразований имеем
![]() (3.14)
(3.14)
где ![]() (рис.
3.16, б);
(рис.
3.16, б); ![]() –
отрезок, отсекаемый рабочей линией на
оси ординат.
–
отрезок, отсекаемый рабочей линией на
оси ординат.
При x = xW y = xW, т.е. рабочая линия исчерпывающей части колонны проходит через точку, лежащую на диагонали с абсциссой xW. Теперь выясним, где же эти линии пересекаются.
Ордината точки пересечения, определяемая по уравнениям (3.13) и (3.14), будет одинаковой. Следовательно, можно приравнять правые части этих уравнений:
![]()
или
![]()
Решая последнее выражение относительно абсциссы с координатой x, после простейших преобразований получаем x = xF, т.е. абсцисса точки пересечения рабочих линий равна составу исходной смеси (т.е. эта точка соответствует сечению, на уровне которого подают питание в колонну). После этого можно построить рабочие линии для укрепляющей и исчерпывающей частей колонны.
На
оси абсцисс откладывают заданные
концентрации xF, xD, xW и
находят точки а и с (рис.
3.16). Если величина R задана,
то на оси ординат откладывают отрезок ![]() и
соединяют точку d c
точкой а.
Проведя вертикаль из точки xF до
пересечения с линией ad,
находят точку b пересечения
рабочих линий и соединяют ее с точкой с.
Таким образом, получают рабочие
линии ab –
для укрепляющей и bc –
для исчерпывающей частей колонны.
и
соединяют точку d c
точкой а.
Проведя вертикаль из точки xF до
пересечения с линией ad,
находят точку b пересечения
рабочих линий и соединяют ее с точкой с.
Таким образом, получают рабочие
линии ab –
для укрепляющей и bc –
для исчерпывающей частей колонны.
18. Метод расчёта массообменных колонных аппаратов со ступенчатым контактом фаз, основанный на уравнении массопередачи. Связь локальной эффективности по Мерфри с числом единиц переноса для различных случаев структуры потоков фаз.
Расчет колонных массообменных аппаратов. В основном распространены противоточные аппараты. Рассмотрим колонный аппарат на примере абсорбции
Допущения:
-
Рассматривается перенос одного компонента, остальные компоненты считаем инертными
-
Фазы движутся по модели идеального вытеснения.
Материальный баланс для всего аппарата:
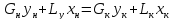 (1)
(1)
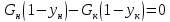 (2)
(2)
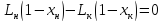 (3)
(3)
 (4)
(4)
Уравнение (4) уже не является независимым, представляя собой сумму первых трёх уравнений.
Материальный баланс для верхней части аппарата:
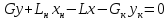 (5)
(5)
 (6)
(6)
Аналогично для нижней части аппарата:
 (6)
(6)
Уравнения (6) – это уравнения рабочих линий (связывают рабочие концентрации в фазах)
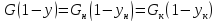 (7)
(7)
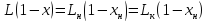 (8)
(8)
Тарельчатая колонна.
 Контакт
фаз ступенчатый.
Контакт
фаз ступенчатый.
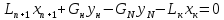
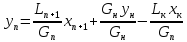 (9)
(9)
 (10)
(10)
 (10)
(10)
Расчёт аппаратов с непрерывной поверхностью контакта фаз
Два основных метода расчёта высоты колонных аппаратов:
-
метод теоретических ступеней
-
метод, основанный на уравнении массопередачи
В результате технологического расчёта получают:
-
высоту аппарата (высота насадки), число тарелок (высота тарельчатой части)
-
сечение аппарата (диаметр)
Объемный расход сплошной фазы
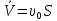
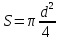
В экстракции расходы обеих фаз.
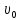 -
фиктивная скорость
-
фиктивная скорость
Метод теоретической ступени разделения
Теоретическая тарелка – это участок аппарата, который покидают фазы, находящиеся в равновесии.
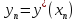
Равновесие определяется P и T
Дано:
абсорбция
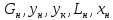
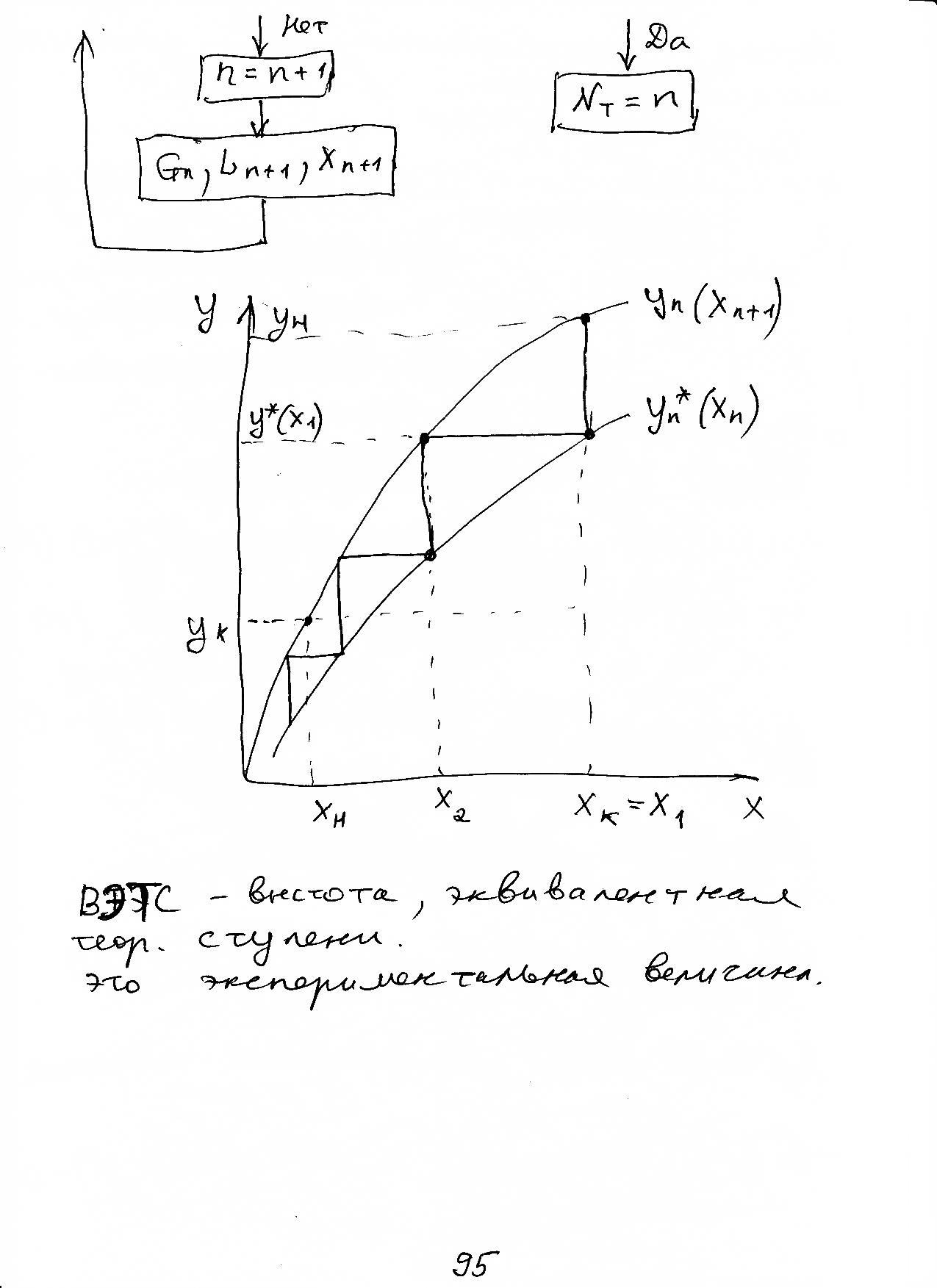
ВЭТС – высота, эквивалентная теоретической ступени. это экспериментальная величина
Метод, основанный на уравнении массопередачи.
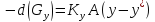

Ky – коэффициент массопередачи по газовой фазе
A – поверхность контакта фаз
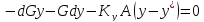 (11)
(11)
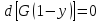 (12)
(12)
По инертному газу
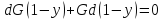
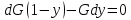 (121)
(121)
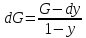
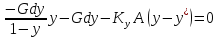
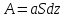
 – удельная
поверхность [м2/м3]
– удельная
поверхность [м2/м3]
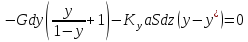
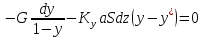
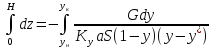
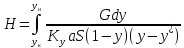 (13)
(13)
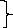

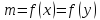
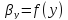
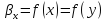


Для жидкой фазы
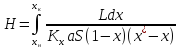 (14)
(14)
Если
линия равновесия прямая
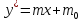 ,
то безразлично по какому из уравнений
считать.
,
то безразлично по какому из уравнений
считать.
Выбирается уравнение для фазы, в которой сосредоточено основное сопротивление.
Частные случаи:
-
Процесс изотермический, концентрации малы
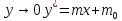
Линия равновесия прямая

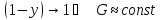
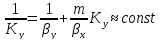
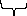
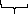
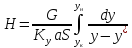 (15)
(15)
hoy noy
noy – общее число единиц переноса по газовой фазе
hoy – высота единиц переноса

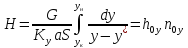
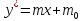 – равновесная
линия прямая
– равновесная
линия прямая
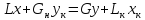
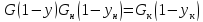
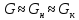
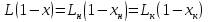
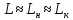
Уравнение рабочей линии
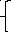
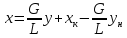 (для
верхней части) (16)
(для
верхней части) (16)
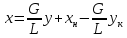 (для
нижней части) (17)
(для
нижней части) (17)
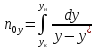



Fm

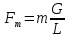 – фактор
массопередачи
– фактор
массопередачи
Отношение наклона равновесной линии
к наклону рабочей линии
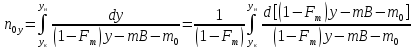
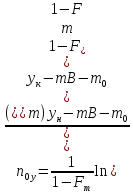
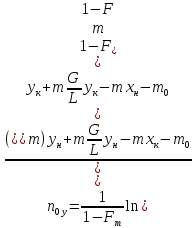
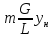 ;
;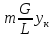 =Fm
=Fm
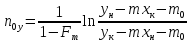 (18)
(18)
-
Fm=1
Наклон равновесной и рабочей линий одинаков
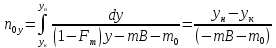
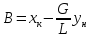 (из
16)
(из
16)
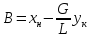 (из
17)
(из
17)
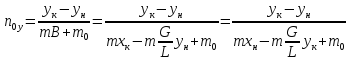
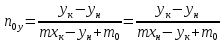 (19)
(19)
-
Концентрации не малы, процесс изотермический, коэффициенты массопередачи слабо зависят от концентрации
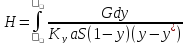
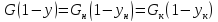
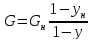
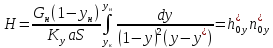 (20)
(20)
Ограничений на кривизну линий не накладывается

Для
постоянного Ky
необходимо,
чтобы
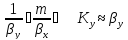
Если
 , то следует записать по жидкой фазе
, то следует записать по жидкой фазе

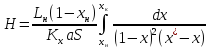 (21)
(21)
Другой случай, когда в обеих фазах МИС

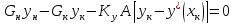
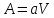
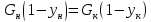
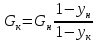
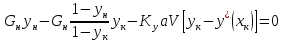
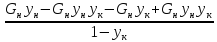
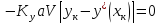
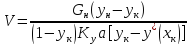
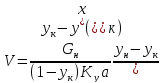
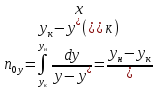 (22)
(22)
(МИС+МИС)
Расчёт высоты колонных аппаратов при ступенчатом контакте фаз
В тарельчатых аппаратах взаимодействие фаз рассматривают только на тарелках. За пределами тарелок фазы не взаимодействуют
-
Метод теоретической тарелки
Фазы, покидающие тарелку, находятся в состоянии равновесия (достигли состояния равновесия)
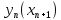 – приходит
на тарелку,
– приходит
на тарелку,
 – покидает тарелку, Ŋ – средний КПД
ступени по колонне,
– покидает тарелку, Ŋ – средний КПД
ступени по колонне,
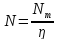 – число
реальных тарелок
– число
реальных тарелок
-
Метод, основанный на понятии коэффициента массопередачи (на уравнении массопередачи)

-
КПД Мерфри
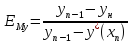
Показывает, во сколько реальное изменение концентрации отличается от изменения концентрации на теоретической тарелке
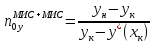 (22)
(22)
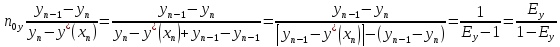
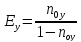 (23)
(23)

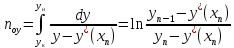
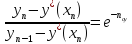
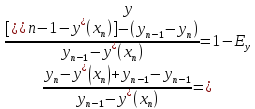
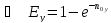 (24)
(24)
E0 – локальная эффективность по Мерфри (без учёта реальных факторов брызгоуноса, байпасирующей жидкости и др.)
EMy – реальный КПД Мерфри
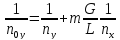
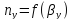
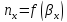
19. Вывести формулу для расчета минимального флегмового числа при непрерывной ректификации. Какие принципы используют для оптимизации при определении флегмового числа?
Упрощающие допущения графического метода анализа работы и расчета ректификационной колонны.
-
Молярные теплоты испарения компонентов при одной и той же температуре приблизительно одинаковы (правило Трутона), поэтому каждый киломоль пара при конденсации испаряет 1 кмоль жидкости. Следовательно количество поднимающихся паров (в киломолях) в любом сечении колонны одинаково;
-
В дефлегматоре не происходит изменения состава пара. Если весь пар конденсируется в дефлегматоре, то это положение полностью соответствует реальным условиям. Следовательно, состав пара, уходящего из ректификационной колонны, равен составу дистиллята, т.е.
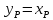 ;
; -
При испарении жидкости в кипятильнике не происходит изменения ее состава. Следовательно, состав пара, образующегося в кипятильнике, соответствует составу кубового остатка, т.е.
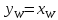 ;
; -
Теплоты смешения компонентов разделяемой смеси равны 0.
Также, при этом перед подачей в колонну смесь подогревают до температуры кипения жидкости в том сечении колонны, в которое она поступает.
Вывод формулы для расчета минимального флегмового числа при непрерывной ректификации
При
пересечении рабочих линий в точке b0
рабочие концентрации равны равновесным,
что возможно только при бесконечно
большой поверхности массопередачи,
так как при этом
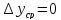 .
.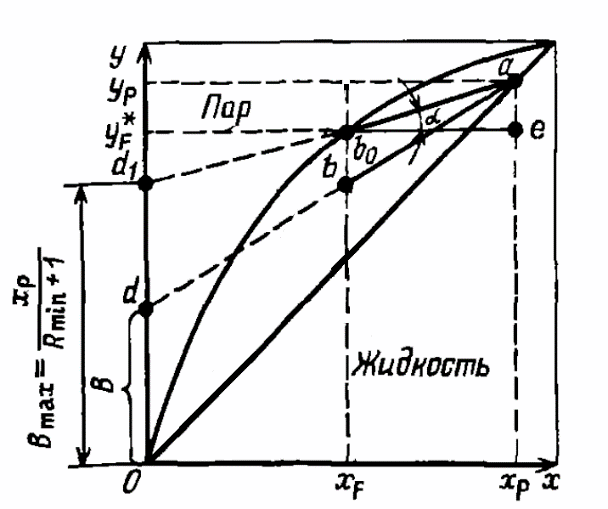
В этом случае (линия ad1 на графике) флегмовое число должно быть минимальным, а величина отрезка B – максимальной.
Уравнение
рабочей линии верхней части колонны:
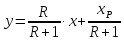
Преобразовав уравнение рабочей линии верхней части колонны к линейному виду, получим:
 ,
где
,
где
 ;
;
В
нашем случае:
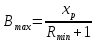 или
или (Bmax
определяется графически)
(Bmax
определяется графически)
Из уравнения рабочей линии верхней части колонны для рассматриваемого случая:
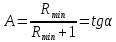
Откуда последует, что:
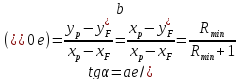
Решая уравнение относительно Rmin, получим: