- •Первые вопросы
- •Вопрос 1 Вывестии дифференциальное уравнение конвективной диффузии. Рассмотреть частный случай диффузии в неподвижной среде.
- •2. Первый закон Фика. Вывод дифференциального уравнения конвективной диффузии.
- •3. Получить диффузионные критерии подобия. Определяемый и определяющие критерии. Физический смысл массообменных критериев подобия.
- •4. Получить уравнение аддитивности диффузионных сопротивлений. Сформулировать допущения при выводе.
- •5. Вывести соотношение между коэффициентами массопередачи и массоотдачи. Из каких уравнений получают коэффициенты массоотдачи?
- •Вопрос №8. Вывод уравнения для расчета средней движущей силы массопередачи.
- •1)Через основное уравнение массопередачи.
- •2) Через число теоретических тарелок.
- •3) Метод кинетической (псевдоравновесной) линии.
- •Вопрос 14. Материальный баланс процесса простой перегонки. Расчет количества кубового остатка, количества и среднего состава дистиллята.
- •16. Вывести уравнение рабочей линии для укрепляющей части ректификационной колонны. Описать, как строят рабочие линии на диаграмме y-X, сформулировав необходимые допущения.
- •Выбор рабочего флегмового числа
- •21. Вывести уравнение теплового баланса ректификационной колонны непрерывного действия. Как определяется расход греющего пара в кипятильнике?
3. Получить диффузионные критерии подобия. Определяемый и определяющие критерии. Физический смысл массообменных критериев подобия.
Основные критерии массобменных процессов аналогичны основным критериям теплообмена.
Рассмотрим
уравнения массопереноса на границе
раздела фаз. Из одной фазы в другую
переходит количество массы, равное
 ,
где
,
где
 -
равновесная концентрация на границе
раздела фаз.
-
равновесная концентрация на границе
раздела фаз.
Это
же количество массы переносится
молекулярной диффузией через пограничный
слой:
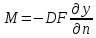
В
этих уравнениях трудноопределимы
величины
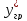 и
n-
толщина пограничного слоя, через который
проходит вещество молекулярной диффузией.
Откуда
и
n-
толщина пограничного слоя, через который
проходит вещество молекулярной диффузией.
Откуда
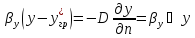
Перемножим на масштабные множители каждый член уравнения:
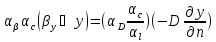
Тогда
 ,
откуда
,
откуда
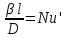 ,
где l-
определяющий геометрический параметр.
,
где l-
определяющий геометрический параметр.
Этот
безразмерный комплекс является аналогом
теплового критерия Нуссельта и называется
диффузионным критерием Нуссельта
(иногда- Шервуда Sh). является определяемым критерием,
поскольку в него входит величина
является определяемым критерием,
поскольку в него входит величина
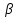 .
Он характеризует отношение скорости
переноса вещества (конвективной и
молекулярной) к молекулярному переносу.
.
Он характеризует отношение скорости
переноса вещества (конвективной и
молекулярной) к молекулярному переносу.
Другие
критерии получим из дифференциального
уравнения конвективной диффузии,
переписав его относительно оси х :
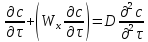
Проведя
его подобное преобразование, получаем
следующие критерии подобия:
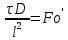 ,
где
,
где
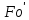 диффузионный
критерий Фурье, который характеризует
подобие неустановившихся процессов
массобмена;
диффузионный
критерий Фурье, который характеризует
подобие неустановившихся процессов
массобмена;
 -
диффузионный критерий Пекле, характеризующий
отношение переноса вещества конвекцией
к молекулярному переносу в сходственных
точках подобных систем. Часто
-
диффузионный критерий Пекле, характеризующий
отношение переноса вещества конвекцией
к молекулярному переносу в сходственных
точках подобных систем. Часто
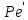 заменяют
отношением:
заменяют
отношением:
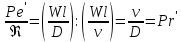 -
диффузионный критерий Прандтля, он
выражает постоянство отношения физических
свойств жидкости или газа в сходственных
точках подобных систем, характеризует
отношение профиля скоростей к профилю
концентраций, т.е. отношение толщины
гидродинамического и диффузионного
пограничных слоев.
-
диффузионный критерий Прандтля, он
выражает постоянство отношения физических
свойств жидкости или газа в сходственных
точках подобных систем, характеризует
отношение профиля скоростей к профилю
концентраций, т.е. отношение толщины
гидродинамического и диффузионного
пограничных слоев.
Для
соблюдения подобия процессов массоотдачи
необходимо также соблюдение
гидродинамического подобия. Поэтому
критериальное уравнение массоотдачи
для неустановившегося процесса будет
иметь вид (Г-геометрический
симплекс):
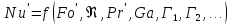
При
установившимся процессе и при отсутствия
влияния сил тяжести (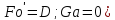 :
:

Например
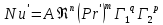
4. Получить уравнение аддитивности диффузионных сопротивлений. Сформулировать допущения при выводе.
Рассмотрим случай переноса вещества из фазы Фу фазу Фх; движущая сила массопередачи выражена в единицах концентрации фазы Фу. Количество вещества М, переносимое из фазы в фазу, рассчитываем из уравнения массопередачи. Допустим, что равновесная зависимость между концентрациями в фазах линейна, линия равновесия описывается уравнением у* = mx, где m – тангенс угла наклона линии равновесия.
Примем, что концентрации распределяемого вещества в фазах у границы раздела (хгр , угр) равновесны друг другу. Тогда из уравнения линии равновесия следует, что хгр = угр/m и х = у*/m, где хгр. и угр - концентрации каждой фазы, у*- концентрация фазы Фу, равновесная с концентрацией х фазы Фх.
Подставляя значения хгр. и х в уравнение массоотдачи М=βx F(xгр-x),
Получим
М=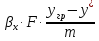
Откуда
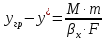
Вместе с тем из уравнения массоотдачи М=βyF(y-yгр), имеем:
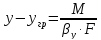
Суммируем, почленно уравнения получим:
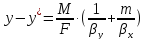
Из
уравнения массопередачи
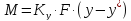 находим :
находим :
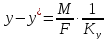
Приравнивания правые части полученных выражений движущей силы (y –y*) и сокращая подобные члены, получим:

При
выражении коэффициента массопередачи
в концентрациях фазы Фх
аналогичные
рассуждения приводят к зависимости