Завдання №5

За допомогою зазначеного методу одновимірної оптимізації на заданому інтервалі і з заданою точністю ps знайти мінімальне значення функції цілі F(x):

1.Метод Фібоначі F(x)=(1-x2)(2+x) на інтервалі [-2;0] ps=0.1	11. Метод розподілу інтервалу навпіл F(x)= на інтервалі [-2;0] ps=0.1
2. Метод розподілу інтервалу навпіл F(x)=(1-x2)2x на інтервалі [-1. 5;0.5] ps=0.1	12. Метод золотого перетину F(x)= на інтервалі [-2;0] ps=0.1
3. Метод золотого перетину F(x)=(1-x2)5x на інтервалі [-1. 5;0.5] ps=0.1	13. Метод Фібоначі F(x)=(2-x2)(4-x) на інтервалі [1.5;3.5] ps=0.1
4. Метод Фібоначі F(x)= на інтервалі [-2;0] ps=0.1	14. Метод розподілу інтервалу навпіл F(x)=(5-x2)7x на інтервалі [-2. 5;-0. 5] ps=0.1
5. Метод розподілу інтервалу навпіл F(x)= на інтервалі [-2;0] ps=0.1	15. Метод золотого перетину F(x)=(1-x2)(2+x) на інтервалі [-2;0] ps=0.1
6. Метод золотого перетину F(x)=(2-x2)(4-x) на інтервалі [1.5;3.5] ps=0.1	16. Метод Фібоначі F(x)=(1-x2)2x на інтервалі [-1. 5;0.5] ps=0.1
7. Метод Фібоначі F(x)=(5-x2)7x на інтервалі [-2. 5;-0. 5] ps=0.1	17. Метод розподілу інтервалу навпіл F(x)=(1-x2)5x на інтервалі [-1. 5;0.5] ps=0.1
8. Метод розподілу інтервалу навпіл F(x)=(1-x2)(2+x) на інтервалі [-2;0] ps=0.1	18. Метод золотого перетину F(x)= на інтервалі [-2;0] ps=0.1
9. Метод золотого перетину F(x)=(1-x2)2x на інтервалі [-1. 5;0.5] ps=0.1	19. Метод Фібоначі F(x)= на інтервалі [-2;0] ps=0.1
10. Метод Фібоначі F(x)=(1-x2)5x на інтервалі [-1. 5;0.5] ps=0.1	20. Метод розподілу інтервалу навпіл F(x)=(2-x2)(4-x) на інтервалі [1.5;3.5] ps=0.1

Нелінійна багатовимірна безумовна оптимізація

Загальний вигляд задачі:

Необхідно оптимізувати , де .

ОСНОВНІ ВІДОМОСТІ ТА ВИЗНАЧЕННЯ

Визначення: Градієнтом функції називається вектор, проекціями якого на координатні осі служать відповідні приватні похідні функції, тобто: .

Градієнт - це вектор, що вказує напрямок збільшення досліджуваної функції, тому всі методи нелінійної багатовимірної безумовної оптимізації, зв'язані з визначенням або градієнту в цілому, або з визначенням тільки деяких складових градієнту. Довжина градієнту дорівнює найбільшій швидкості зростання функції в цій точці.

На досліджувану функцію накладається обов'язкова умова про те, що функція повинна бути опуклою (для точки мінімуму) або ввігнутою (для точки максимуму).

Множина точок називається опуклою, якщо ця множина разом із будь-якими своїми двома точками містить і весь відрізок, з'єднуючий ці точки.

Функція , якщо визначена на опуклій множині n-мірного простору, називається опуклою на цій множині, якщо

можна дати аналогічне визначення увігнутої функції, при цьому нерівність  поміняється на .

Деякі властивості опуклих і увігнутих функцій:

Якщо функція опукла, то - увігнута, тобто можна перейти від задачі

мінімізації до задачі максимізації, або навпаки, що досягається зміною опуклої функції дослідження на ввігнуту.

1. Якщо існує послідовність опуклих функцій 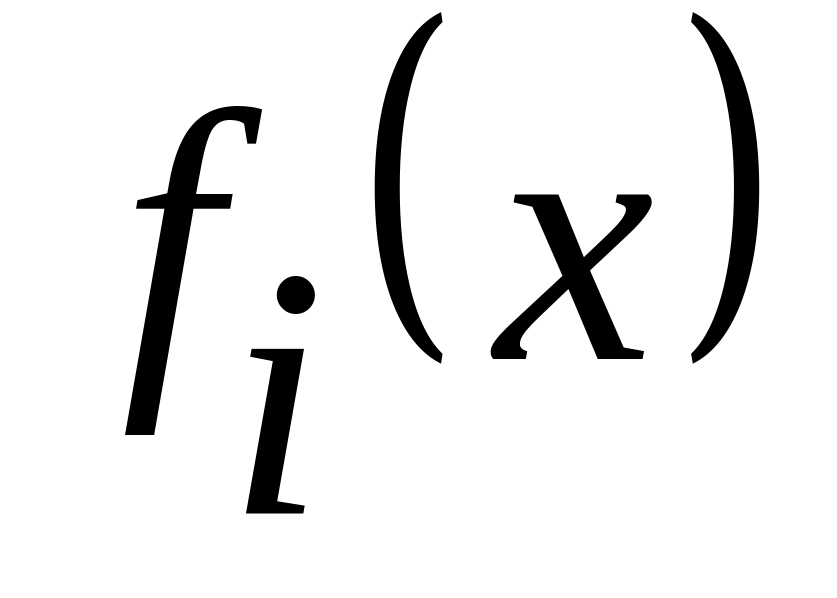для i = 1…n, і при цьому існують довільні значення _і  0, то функція 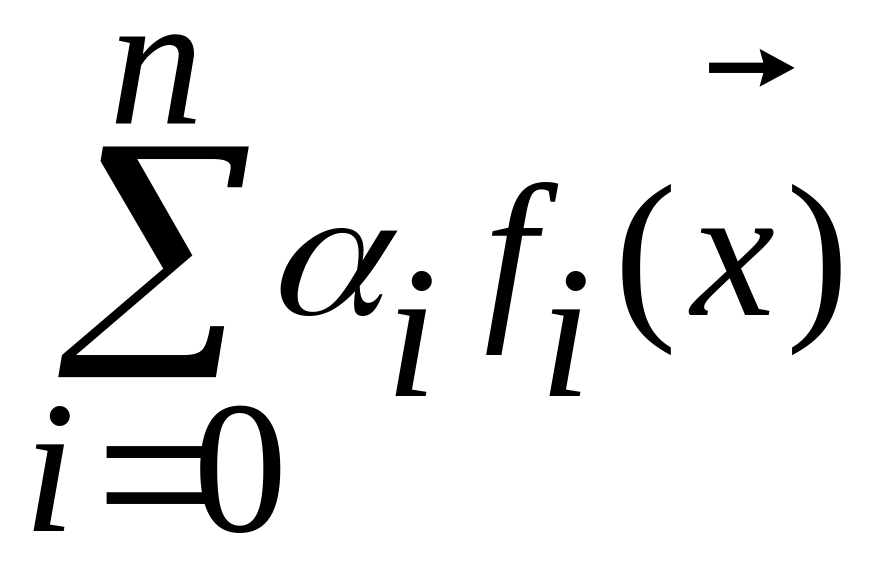теж є опуклою.

2. Опукла або увігнута функція безупинна в кожній внутрішній точці опуклої або увігнутої множини, на якому визначена досліджувана функція.

3. Функція є опуклої в тому і тільки в тому випадку, якщо для будь-якої точки хМ виконується , якщо х_i і х_j не зверта-ються в 0.

Критерій Сильвестра:

Функція є опуклою тоді, коли всі головні мінори матриці інших приватних похідних функції позитивні або нульові значення, у цьому випадку матриця є позитивно визначеною. Функція є увігнутою, якщо знак усіх головних мінорів матриці других приватних похідних чергується, починаючи з «-». При цьому матриця називається негативно визначеною, в усіх інших випадках знак матриці невизначений, тому матриця називається знако-невизначеною.

Будь-яка задача нелінійної багатовимірної безумовної оптимізації на визначення екстремальних значень функції вирішується за допомогою двох основних теорем, які є необхідною і достатньою умовами існування екстремумів функції.

Теорема 1: необхідна умова існування екстремума.

Для того, щоб точка була стаціонарною точкою деякої функції , необхідно, щоб градіент у цій точці дорівнював нулю.

Теорема 2: достатня умова існування екстремума.

Нехай точка стаціонарна, для того,. щоб ця точка була точкою мінімуму досить, щоб матриця Геса (матриця других приватних і змішаних похідних) була позитивно визначена. Для точки максимуму досить, щоб матриця Гесса була негативно визначеною.

Загальний вигляд матриці Гесса:

Матриця Гесса симетрична, через те, що для безупинних функцій неважливий порядок взяття приватних та змішаних похідних.

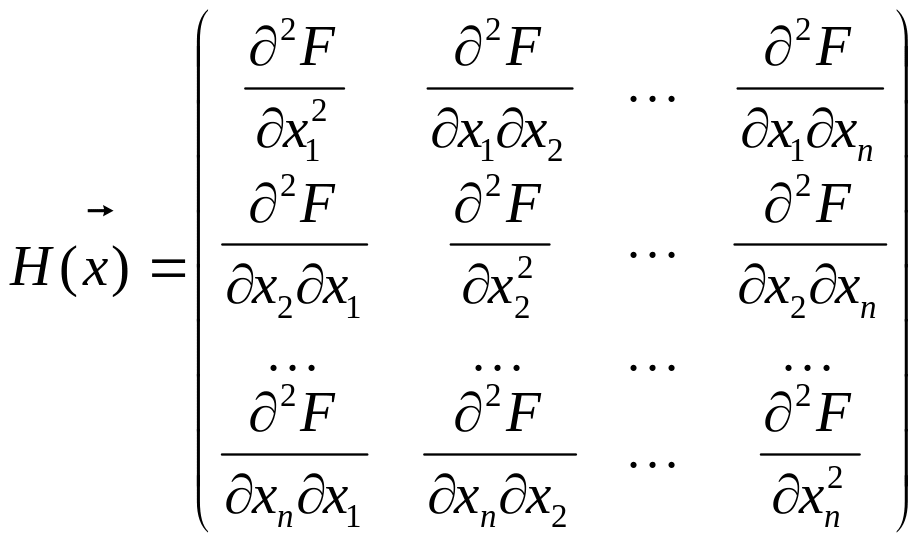
Серед методів багатовимірної безумовної оптимізації розрізняють точні та наближені.

МЕТОД ЕЙЛЕРА

Це точний метод, який дозволяє досліджувати функцію і визначити будь-які екстремальні значення функції (мінімум, максимум, точки перегину).

Метод цілком побудований на необхідній і достатній умовах існування екстремума функції і умовно складається з двох кроків:

1-й крок. Визначаємо аналітичний вигляд градієнту функції, прирівнюємо всі складники градієнту до нуля і визначаємо стаціонарні точки функції, вирішуючи нелінійну систему рівнянь.

2-й крок. Будуємо матрицю Гесса. Визначаємо її числовий вид і знак для кожної точки, визначеної на першому кроці, тим самим класифікуємо стаціонарні точки за критерієм Сильвестра .

Наприклад. Знайти всі стаціонарні точки заданої функції та класифікувати їх тип.

Розвязок. Побудуємо систему часткових похідних функції, які прирівнюємо до нуля. У результаті отримуємо систему нелінійних рівнянь:

де - стаціонарні точки функції. Класифікуємо їх за допомогою матриці Гесса, загальний вигляд якої . Для класифікації точок підставимо їх координати в матрицю Гесса:

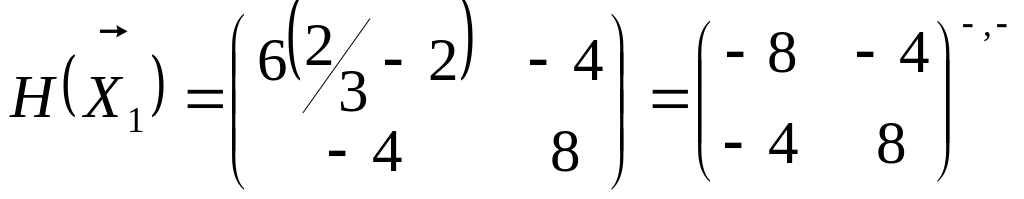, тоді - точка перегину функції , тоді - точка мінімуму функції.

НАБЛИЖЕНІ МЕТОДИ БЕЗУМОВНОЇ БАГАТОВИМІРНОЇ НЕЛІНІЙНОЇ ОПТИМІЗАЦІЇ

Необхідно оптимізувати де .

До вихідної задачі необхідно ще додати початкове наближення до точки оптимуму і точність обчислення >0.

Метод Ньютона

Заснований на послідовному визначенні точок за допомогою рекурентного співвідношення: , де

- зворотня матриця Гесса в точці

- градіент у точці

Наближеною точкою оптимуму будемо вважати ту, значення градієнту в якій по модулю менше або дорівнює . При визначенні точок відбувається перебір припустимих значень точки оптимуму по напрямку антиградієнта функції, тобто по напрямку зменшення значення функції цілі. На цьому принципі заснований будь-який градієнтний наближений метод оптимізації.

Метод дає швидке рішення задачі, якщо початкове наближення задане якнайближче до точки оптимуму.

Недоліком методу є визначення значення зворотної матриці на кожному кроці визначення значень поточної точки.

Метод найскорішого спуску

Цей метод є модифікацією методу Ньютона. Не вимагає використання матриці Геса для обчислень і добре дає наближення в тому випадку, якщо початкова точка віддалена від точки оптимуму.

Обчислення координат точок ведуться по наступному рекурентному співвідношенню: .

Умова завершення перерахунку така ж, сама і в методі Ньютона.

 визначається як точка мінімуму функції

Функція, використовувана для визначення значення , залежить тільки від , тому її оптимізацію можна виконувати за допомогою будь-якого методу одновимірної безумовної оптимізації.

Метод покоординатного спуску

У методі покоординатного спуску координати точки визначаються кожна окремо, причому отримане значення i-й координати використовується при визначенні i+1-й координати. Умова завершення підрахунку точок така ж, сама як і в усіх наближених градієнтних методів: точки перераховуємо доти, поки градієнт у деякій к-ій точці по модулю не буде менше або дорівнюватиме заданої точності. Тоді точка вважається точкою мінімуму. Необхідно порахувати значення функції в цій точці.

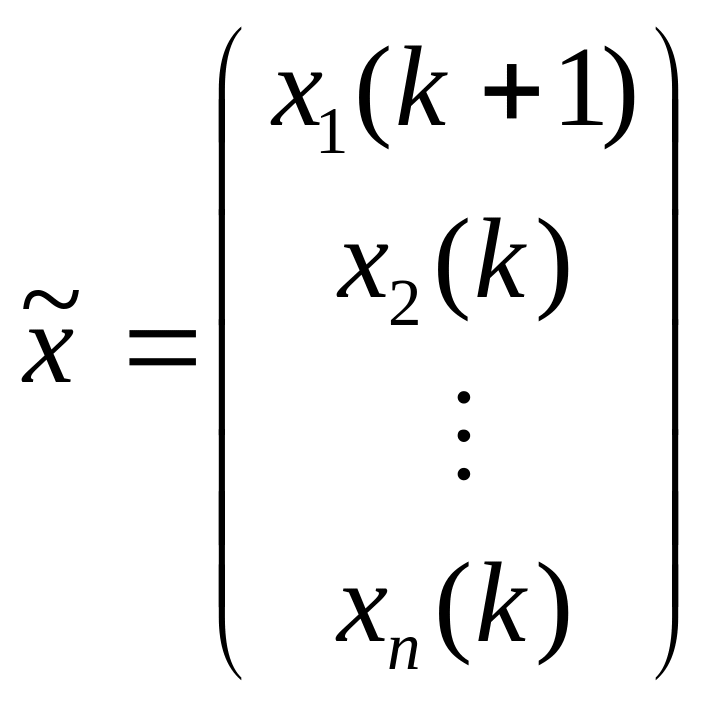; ; -проміжна точка;

;

; ; ;

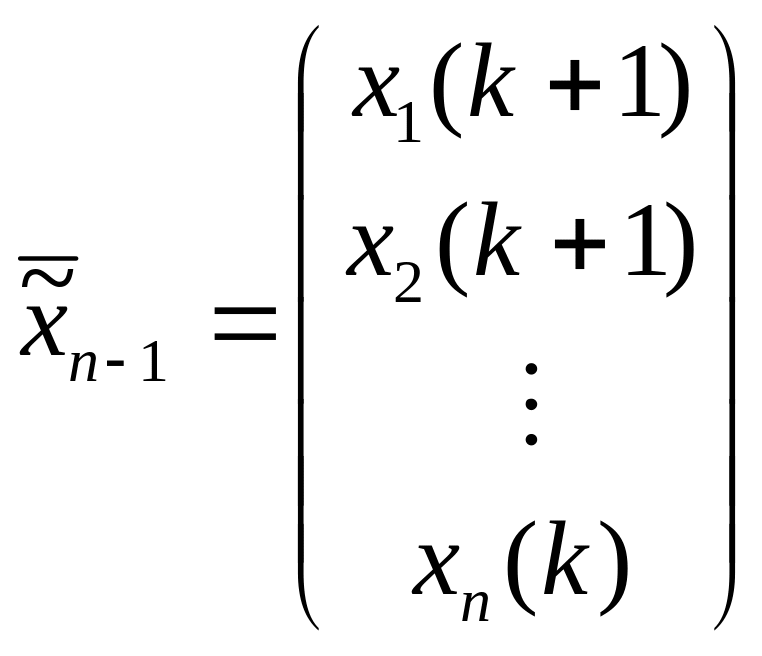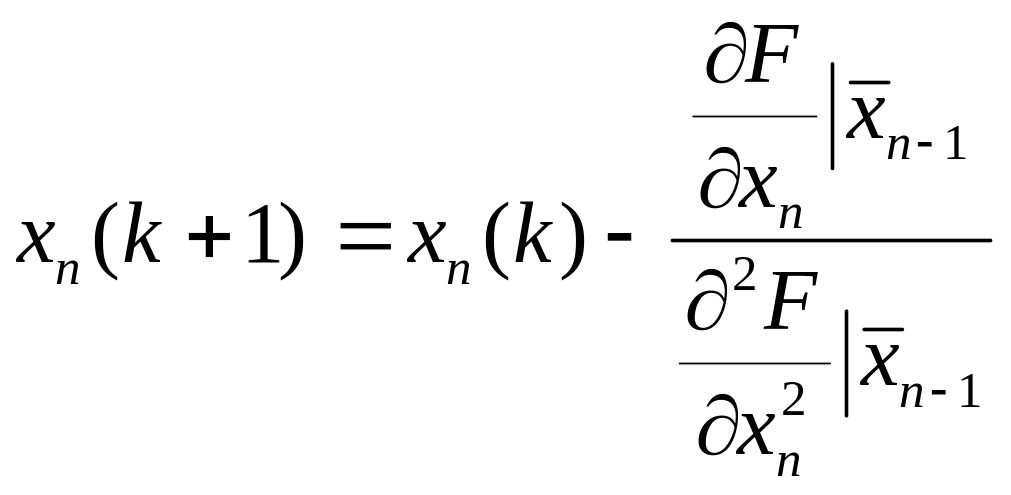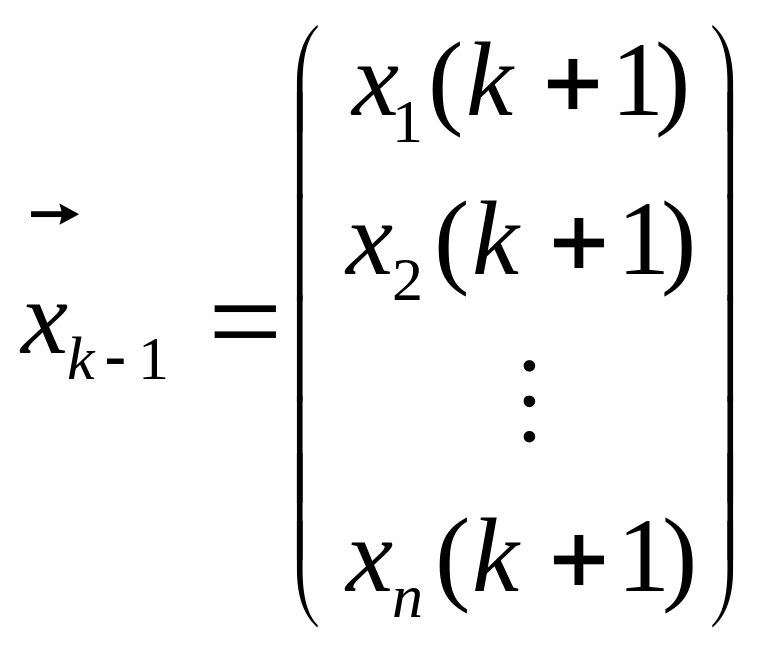Розглянемо використання наближених методів багатовимірної оптимізації на прикладі тієї самої функції , якщо задано початковий вектор та точність =0.2

Розрахунки проводимо за допомогою пакету MathCad, тому використаємо його символіку.

П орівнюючи мінімальні значення функції, які були отримані різними методами, можна бачити, що вони практично однакові, але кожен метод потребує своєї кількості кроків для досягнення необхідної точності.