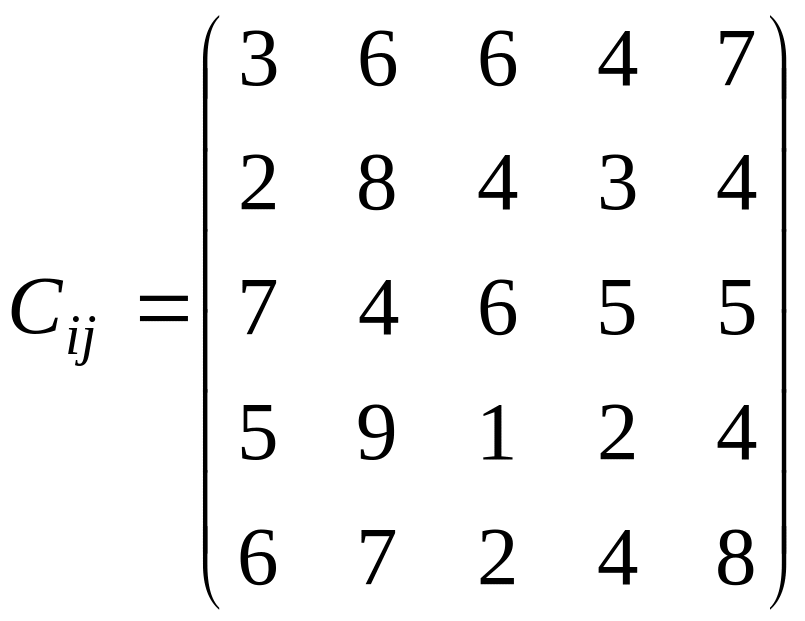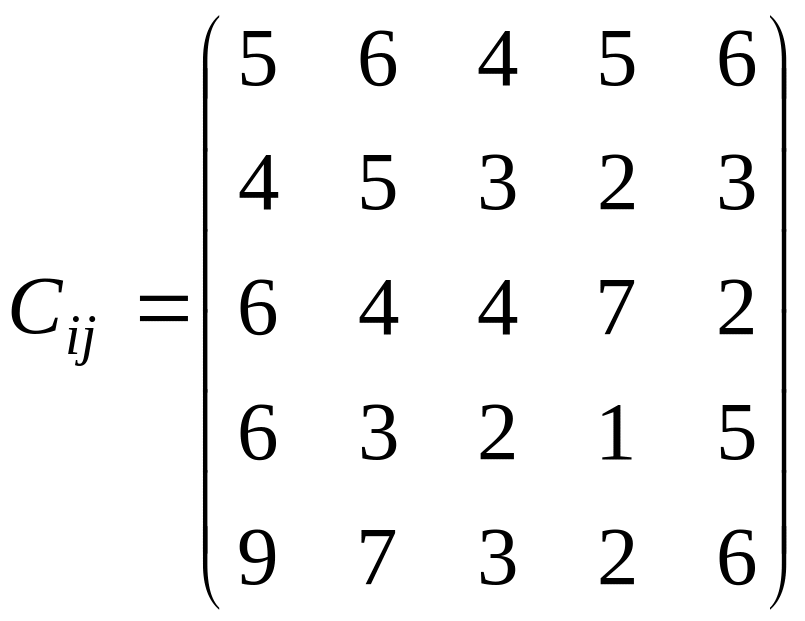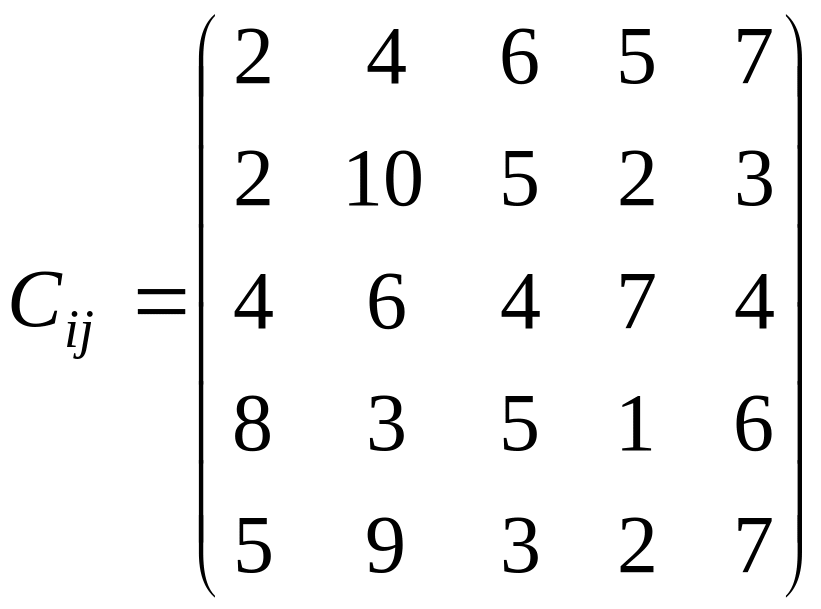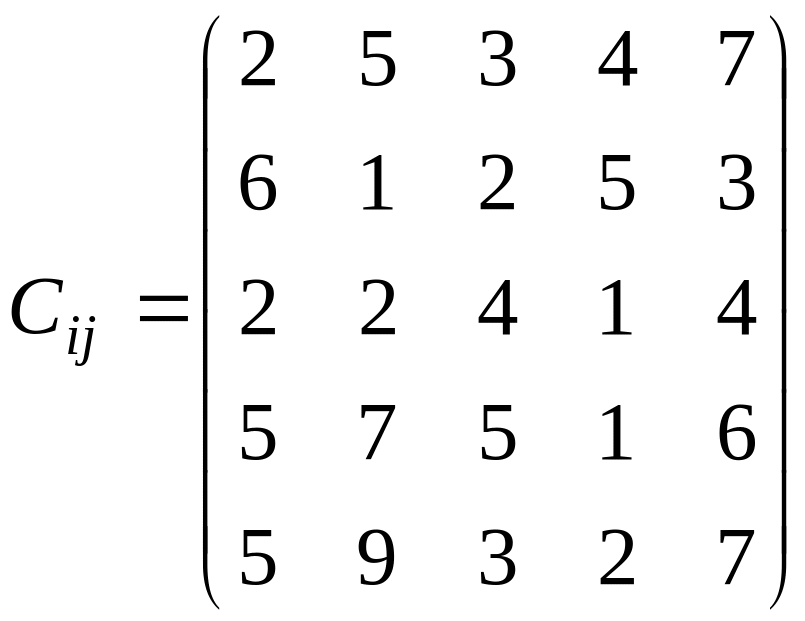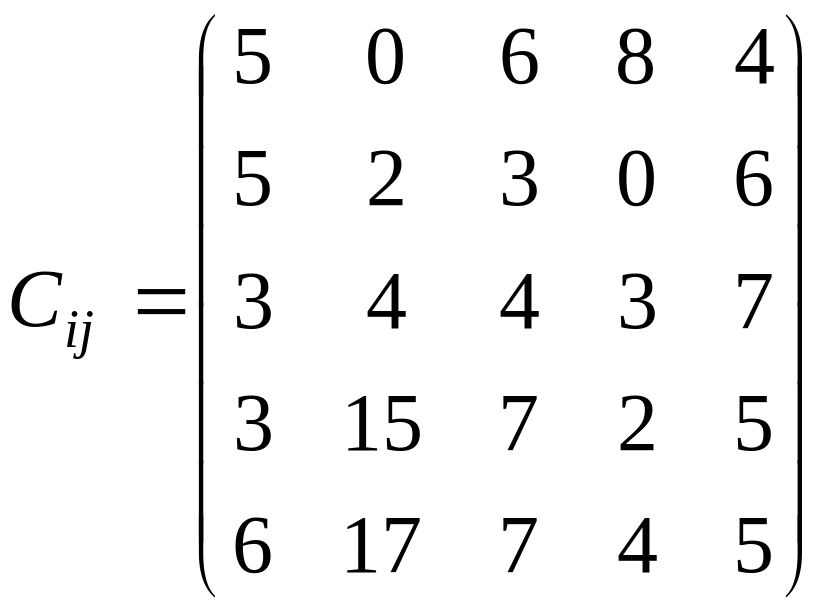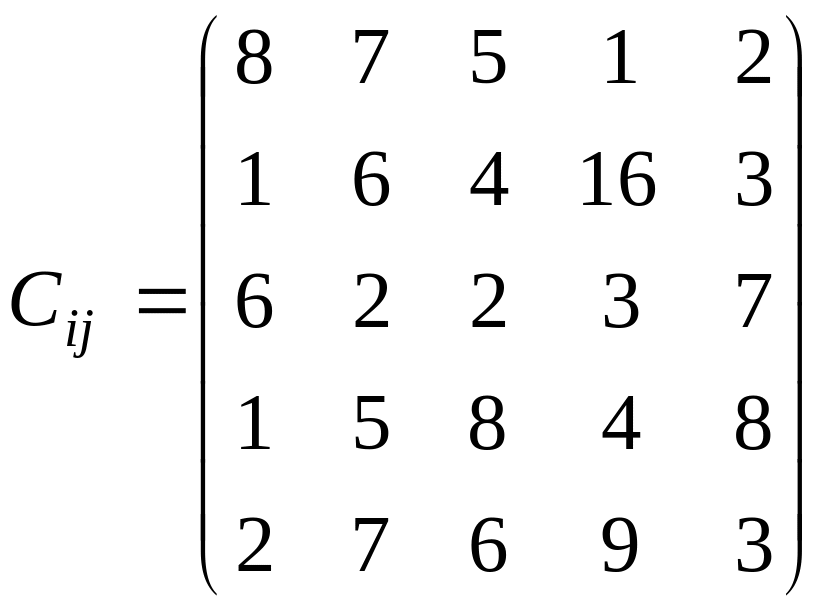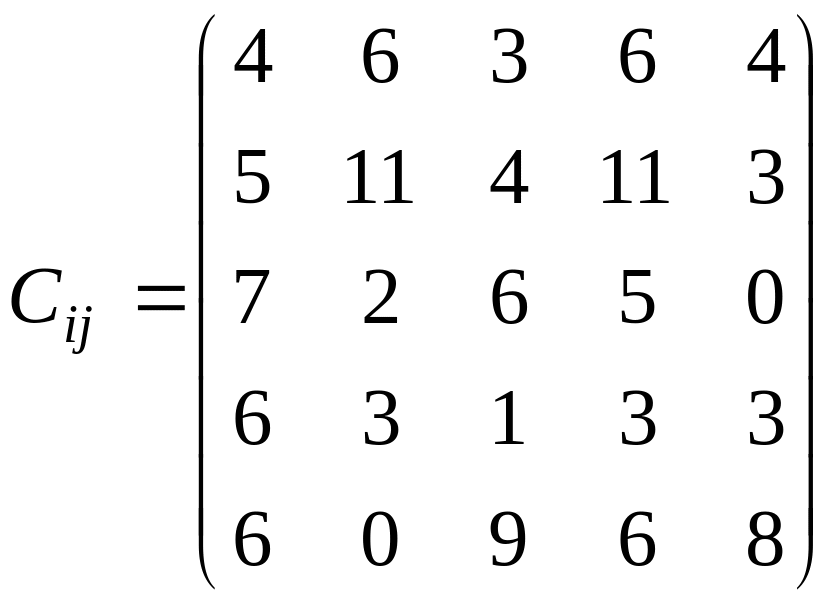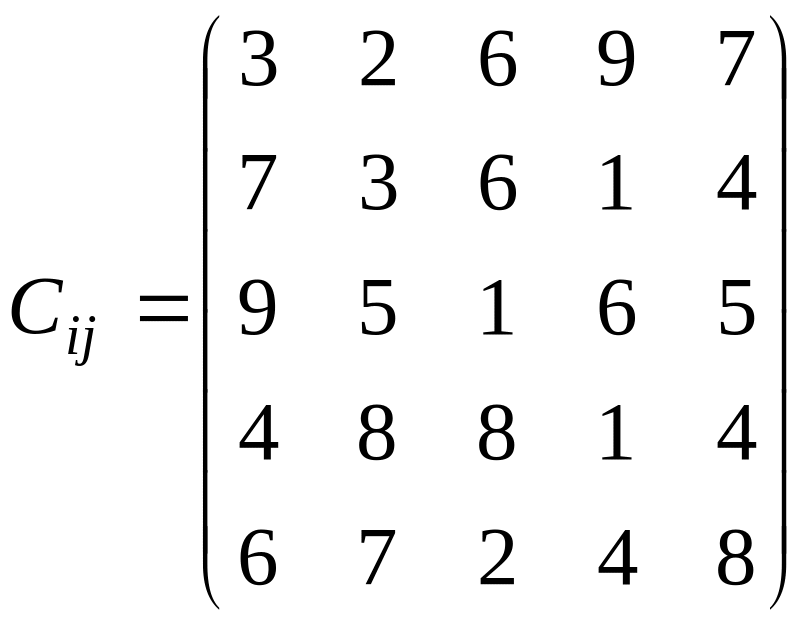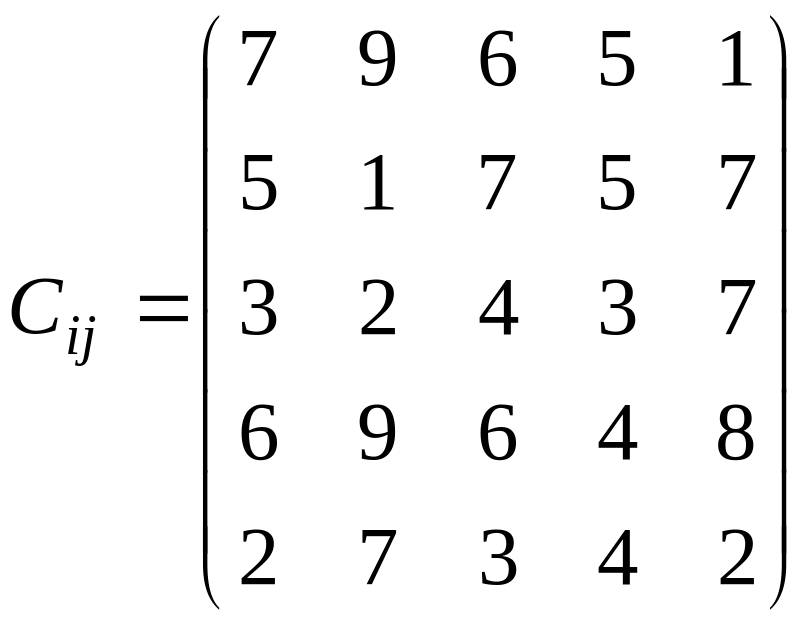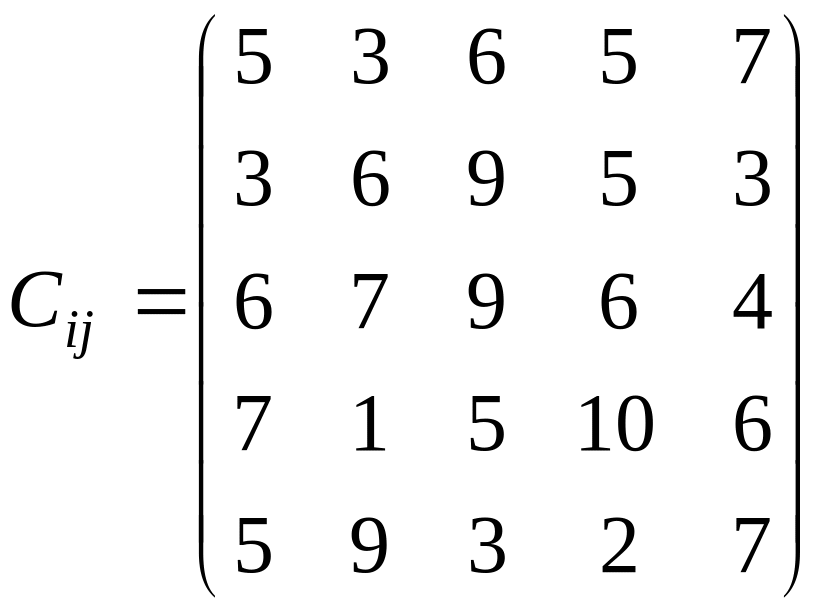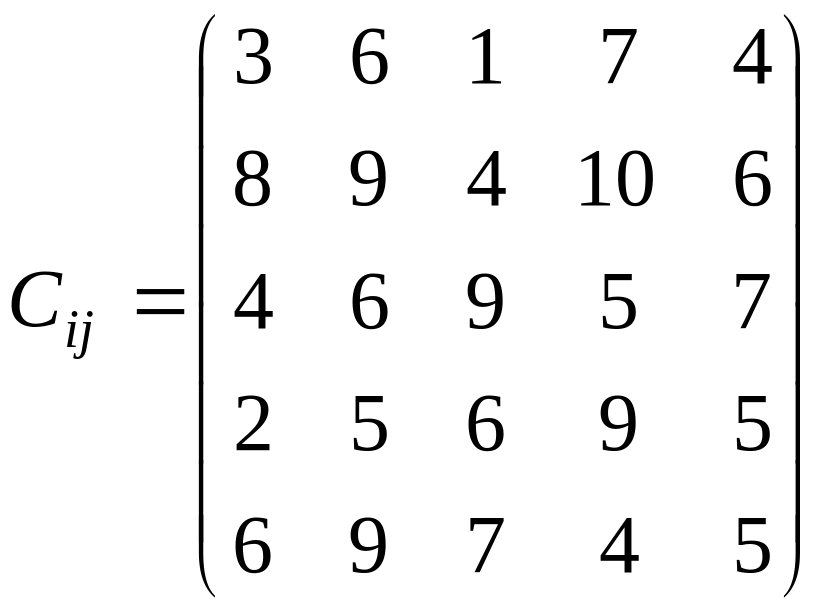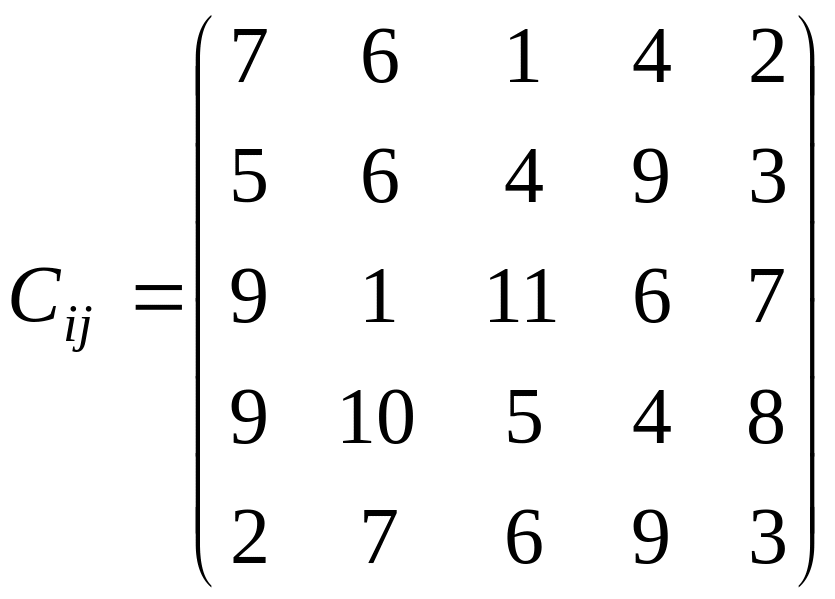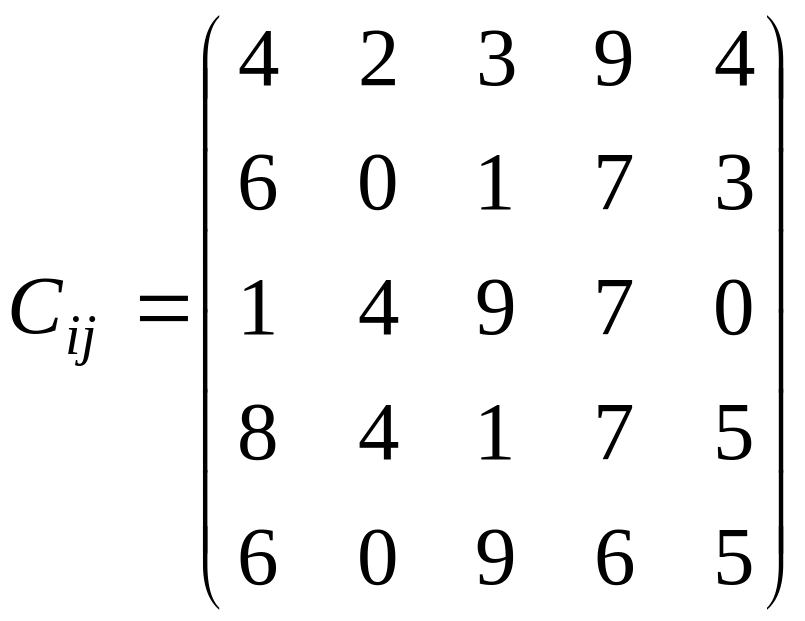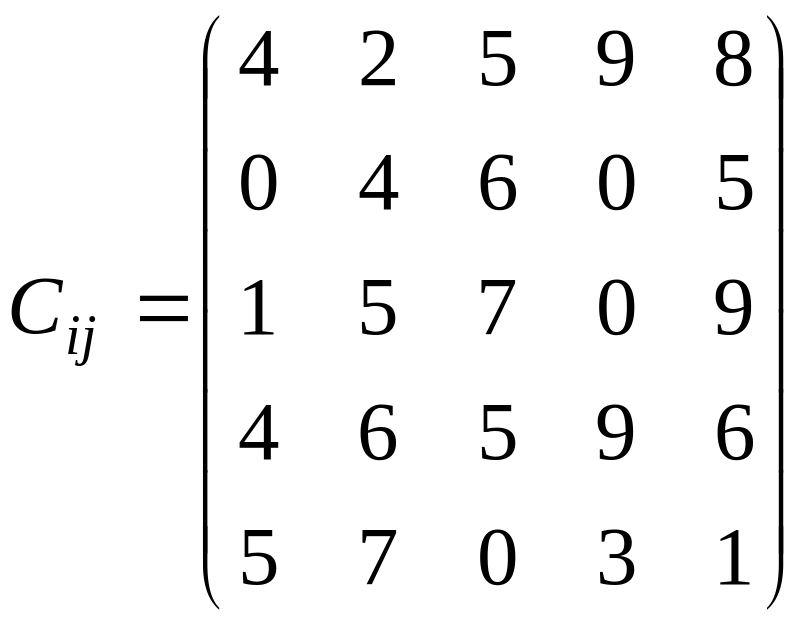Завдання №4

У розподільній системі опрацювання даних у деякий момент часу є n ресурсів готових до виконання завдань. У систему надходить n завдань. Відома якість виконання завдань кожним ресурсом (коефіцієнти матриці С). Потрібно призначити кожному ресурсу своє завдання таким чином, щоб якість виконання всіх завдань була максимальною.

1	11
2	12
3	13
4	14
5	15
6	16
7	17
8	18
9	19
10	20

Частина 2. Нелінійне програмування методи одновимірної пошукової оптимізації

Задача оптимізації, в котрій характеристична міра задана функцією однієї змінної, належить до найбільш простого типу оптимізаційних задач. Проте аналіз задач такого типу займає центральне місце в оптимізаційних дослідженнях як теоретичної, так і практичної спрямованості. Це пов'язано не тільки з тим, що одномірна оптимізація часто використовується для аналізу підзадач, що виникають при реалізації ітеративних процедур, орієнтованих на рішення багатовимірних задач оптимізації.

ВЛАСТИВОСТІ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

для всіх

У теорії оптимізації f називається цільовою функцією, а S - припустимою областю, множиною точок, що задовольняють обмеженням, або областю припустимих значень x.

В інженерних додатках існують такі випадки, коли доводиться використовувати розривні функції. Очевидно, залежно від того, чи є дослід-жувана функція безупинною або розривною, а також залежно від структури припустимої області для реалізації процедури пошуку точок оптимуму функції варто використовувати різні методи

Монотонні функції. Функція f(x) є монотонною (як при зростанні, так і при убуванні), якщо для двох довільних точок x1 і x2 , таких, що x1  x2, виконуються одна з наступних нерівностей:

(монотонно зростаюча функція),

(монотонно спадна функція).

Визначення. Функція f(x) є унімодальною на відрізку a  x  b у тому і тільки тому випадку, якщо вона є монотонною з обох сторін від єдиної на розглянутому інтервалі оптимальної точки . Іншими словами, якщо - єдина точка мінімуму f(x) на відрізку a  x  b , то f(x) виявляється унімодальною на даному інтервалі тоді і тільки тоді, коли для точок x1 і x2

із випливає, що ,

і

з випливає, що .

Унімодальна функція не обов'язково повинна бути безупинною.

КРИТЕРІЇ ОПТИМАЛЬНОСТІ

Функція f(x), визначена на множині S, досягає свого глобального мінімуму в точці  S у тому і тільки тому випадку, якщо для всіх x  S.

Функція f(x), визначена на множині S, має локальний мінімум (відносний мінімум) у точці  S у тому і тільки тому випадку, якщо для всіх x , віддалених від на відстань , тобто якщо існує   0, таке, що для всіх x , що задовольняють умові , виконується нерівність .

( 1. Якщо функція має властивість унімодальності, то локальний мінімум автоматично є глобальним мінімумом.

2. Якщо функція не є унімодальною, то можлива наявність декількох локальних оптимумів; при цьому глобальний мінімум можна визначити шляхом перебору всіх локальних оптимумів і вибору найменшого з них.)

Теорема. Необхідна та достатня умови того, що x* є точкою локального мінімуму (максимуму) функції f, що двічі диференцюється на відкритому інтервалі (a , b), виражаються наступним співвідношеннями:

1. 

2.

Стаціонарною точкою називається точка , для якої

Теорема. Нехай у точці перші (n-1) похідні функції звертаються в нуль, а похідна порядку n відмінна від нуля.

1. Якщо n - непарне, те - точка перегину.

2. Якщо n - парне, те - точка локального оптимуму.

Крім того,

(а) якщо ця похідна позитивна, то - точка локального мінімуму;

(б) якщо ця похідна негативна, то - точка локального максимуму.

НАБЛИЖЕНІ МЕТОДИ ОДНОВИМІРНОЇ БЕЗУМОВНОЇ ОПТИМІЗАЦІЇ

У тому випадку, якщо пошук екстремуму функції класичним методом з використанням необхідної та достатньої умов є неможливим, можна застосувати один з наближених методів одновимірної безумовної оптимізації. Для цього спочатку необхідно визначити інтервал існування точкі екстремуму, а потім проводити пошук згідно алгоритму обраного методу.

Метод розподілу інтервалу навпіл.Розглянутий метод дозволяє виключати в точності половину інтервалу на кожній ітерації. Іноді цей метод називають трьохарапковим пошуком на рівних інтервалах, оскільки його реалізація заснована на виборі трьох спробних точок, рівномірно розподілених в інтервалі пошуку.

Алгоритм методу:

• Покласти xm =(a +b)/2 і L =b-a. Обчислити значення f(xm ).

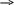• Покласти x1=a+L/4 і x2=b-L/4. Зауважимо, що точки x1, x2 і xm поділяють інтервал (a ,b) на чотири рівні частини. Обчислити значення f(x1) і f(x2).

• Порівняти f(x1), f(x2) і f(xm).

Якщо f(x1)< f(xm), виключити інтервал (xm ,b)­­­­ , поклавши b =xm. Середньою точкою інтервалу пошуку стає точка x1. Отже, необхідно покласти xm=x1 і f(xm)=f(x1).

Якщо f(x2)< f(xm), виключити інтервал (a ,xm)­­­­ , поклавши a =xm. Середньою точкою інтервалу пошуку стає точка x2. Отже, необхідно покласти xm=x2 і f(xm)=f(x2).

Якщо f(x1) f(xm) і f(x2)  f(xm), виключити інтервал (a ,x1) і (x2 ,b)­­­­ . Покласти a=x1 і b=x2 . Зауважимо, що xm продовжує залишатися середньою точкою нового інтервалу.

• О бсислити L=b-a. Якщо розмір L заданої точності Eps, закінчити пошук. У противному випадку повернутися до пункту, позначеного

• У якості точки оптимуму вибрати точку Х_опт. = xm, Fопт_. = f(xm).

Метод золотого перетину.Схема пошуку, при котрій спробні точки поділяють інтервал у відношенні   0. 61803, відома за назвою пошуку за допомогою методу золотого перетину. Зауважимо, що після двох обчислень значень функції кожне наступне обчислення дозволяє виключити підінтервал, розмір якого складає (1-)-ю частку від інтервалу пошуку.

Алгоритм методу:

• Покласти L =b-a, 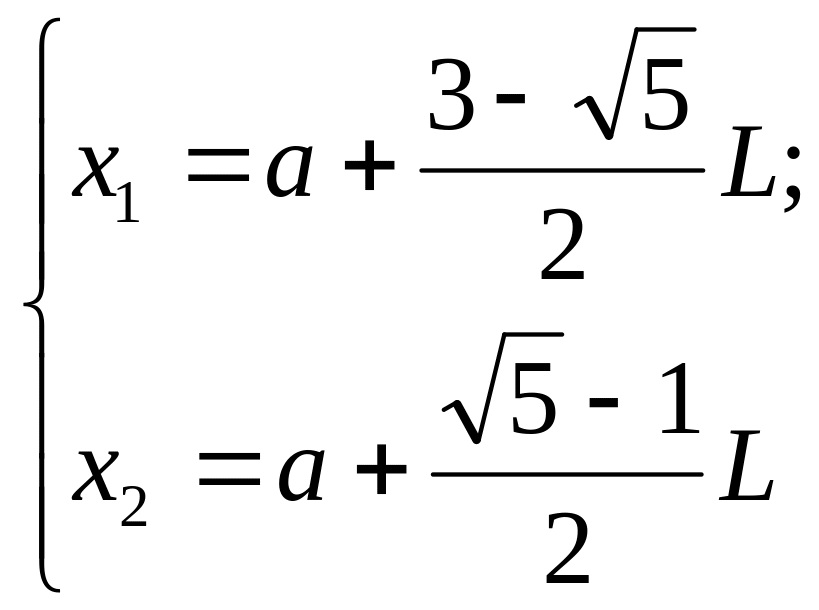. Обчислити значення f(x1 ), f(x2).

• Порівняти f(x1), f(x2).

Якщо f(x1)> f(x2), виключити інтервал (а, x1)­­­­ , поклавши а=x1, x1=x2, f(x1)=f(x2), L =b-a . Обчислити x2 і f(x2) за формулами, згаданими раніше.

Якщо f(x1)  f(x2), виключити інтервал (x2 ,b)­­­­ , поклавши b =x2 , x2=x1 , f(x2)=f(x1), L =b-a . Обчислити x1 і f(x1) за формулами, згаданими раніше.

• Якщо розмір L заданої точності Eps, закінчити пошук. У противному випадку повернутися до

• Як точку оптимуму вибрати точку Х_опт. =(a+b)/2. Обчислити значення функції в цій точці.

Метод Фібоначі. Схема пошуку заснована на підрахунку і використанні чисел Фібоначі, що обчислюються за наступним правилом: наступне число Фібоначі дорівнює сумі двох попередніх чисел

F1=F2=1, Fi₊₂ =Fi + Fi₊₁ , для будь-якого значення i  1.

{ 1, 1, 2 (1+1), 3(1+2), 5(2+3), 8(3+5), 13(5+8), 21 і т.д. }

Алгоритм методу:

• Обчислювати числа Фібоначі доти, поки не виконається наступна умова 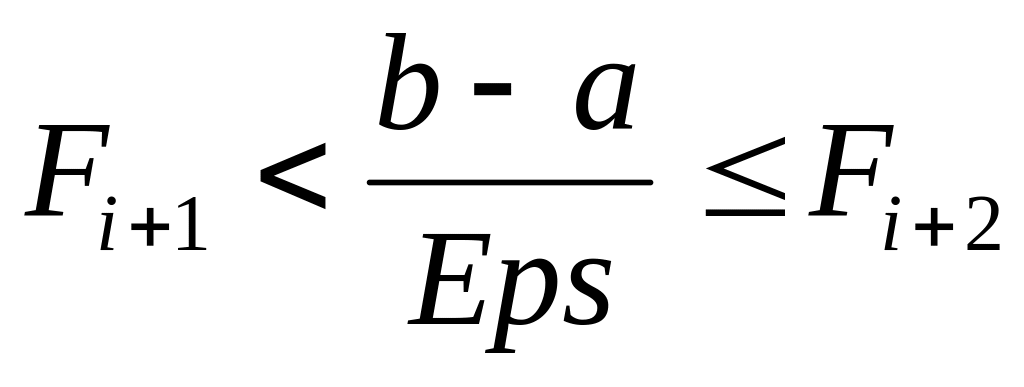. Надалі необхідно буде виконати N=i кількість ітерацій (першою ітерацією є підготовчий етап).

• Підготовчий етап: обчислити, L= b-a,

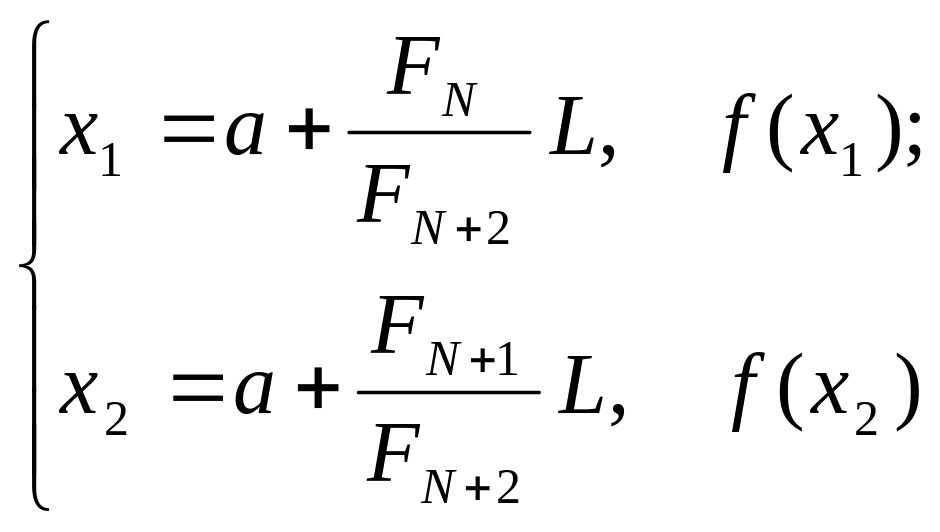
• Для к від к=2 до к=N.

Порівняти f(x1), f(x2).

Якщо f(x1)> f(x2), виключити інтервал (а ,x1)­­­­ , поклавши а =x1, x1=x2, f(x1)=f(x2). Обчислити .

Якщо f(x1)  f(x2), виключити інтервал (x2 ,b)­­­­ , поклавши b =x2 , x2=x1 , f(x2)=f(x1). Обчислити .

Збільшити значення к на одиницю.

• Закінчити пошук. Точкою оптимуму буде точка Х_опт. =х₁=х₂. Обчислити значення функції в цій точці.

Для зручності виконання завдання всі обчислення краще заносити в таблицю наступного виду:

• для методу розподілу інтервалу навпіл:

№ ітерац.

A

b

L=b-a

X1

Xm

X2

F(X1)

F(Xm)

F(X2)

• для методу золотого перетину:

№ ітерац.

A

b

L=b-a

X1

X2

F(X1)

F(X2)

• для методу Фібоначі:

№ ітерац.

A

b

X1

X2

F(X1)

F(X2)

Розглянемо наступну задачу:

на інтервалі [90;120] з точністю Еps =1.

Метод розподілу інтервалу навпіл:

№ іт.	а	B	L = b-a	X1	Xm	X2	F(X1)	F(Xm)	F(X2)
1	90	120	30	97.5	105	112.5	2.52	52	12.52
2	90	105	15	93.75	97.5	102.25	6. 252	2.52	2. 252
3	97.5	105	7.5	100.37	102.25	104.12	0. 372	2. 252	4. 122
4	97.5	102.25	3.75	99.43	100.37	101.01	0. 572	0. 372	1. 012
5	99.43	101.01	1.87	99.9	100.37	100.84	0.12	0. 372	0. 842
6	99.43	100.37	0.94		99.9			0.01

На 6-й ітерації довжина відрізка L  0.94 < Eps. Отже, задача вирішена: точка мінімуму х  99.9, значення функції в цій точці Lmin0.01.

Метод золотого перетину:

	а	b	L = b-a	X1	X2	F(X1)	F(X2)
1	90	120	30	101.46	108.54	1. 462	8. 542
2	90	108.54	18.54	97.08	101.46	2. 922	1. 462
3	97.08	108.54	11.46	101.46	104.16	1. 462	4. 162
4	97.08	104.16	7.08	99.78	101.46	0. 222	1. 462
5	97.08	101.46	4.38	98.75	99.78	1. 252	0. 222
6	98.75	101.46	2.71	99.78	100.42	0. 222	0. 422
7	98.75	100.42	1.67	99.39	99.78	0. 612	0. 222
8	99.39	100.42	1.03	99.78	100.03	0. 222	0. 032
9	99.78	100.42	0.64	100.03		0. 032

На 9-й ітерації довжина відрізка L  0.64 < Eps. Отже, задача вирішена: точка мінімуму х = (99.78+100. 42)/2  100. 1, значення функції в цій точці Lmin 0.01.

Метод Фібоначі :

(b-a)/Eps = 30; F1=F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21, F9=34.

F8=21<30< F9=34, отже, необхідно буде виконати 9-2=7 ітерацій для досягнення необхідної точності Eps ( N=7 ).

K	а	b	X1	X2	F(X1)	F(X2)
1	90	120	101.47	108.53	1. 472	8. 532
2	90	108.53	97.06	101.47	2. 942	1. 472
3	97.06	108.53	101.47	104.12	1. 472	4. 122
4	97.06	104.12	99.71	101.47	0. 292	1. 472
5	97.06	101.47	98.82	99.71	1. 182	0. 292
6	98.82	101.47	99.71	100.58	0. 292	0. 582
7	98.82	100.58	99.71	99.71	0. 292	0. 292

У результаті одержуємо: точка мінімуму х  99.71, значення функції в цій точці Lmin0. 0841.