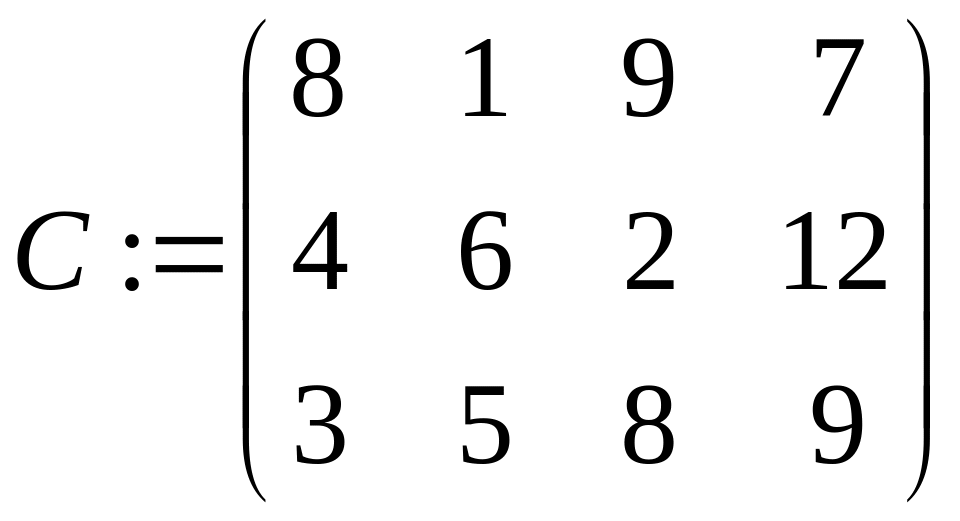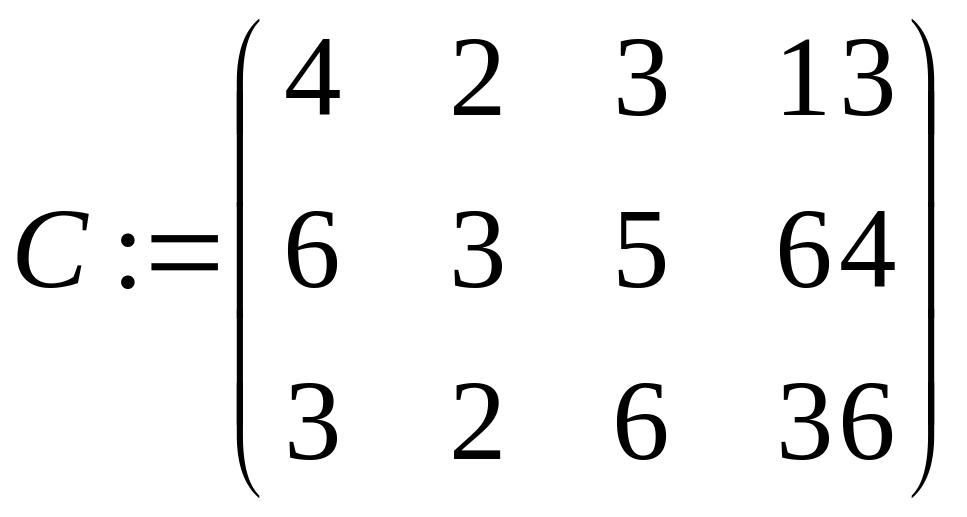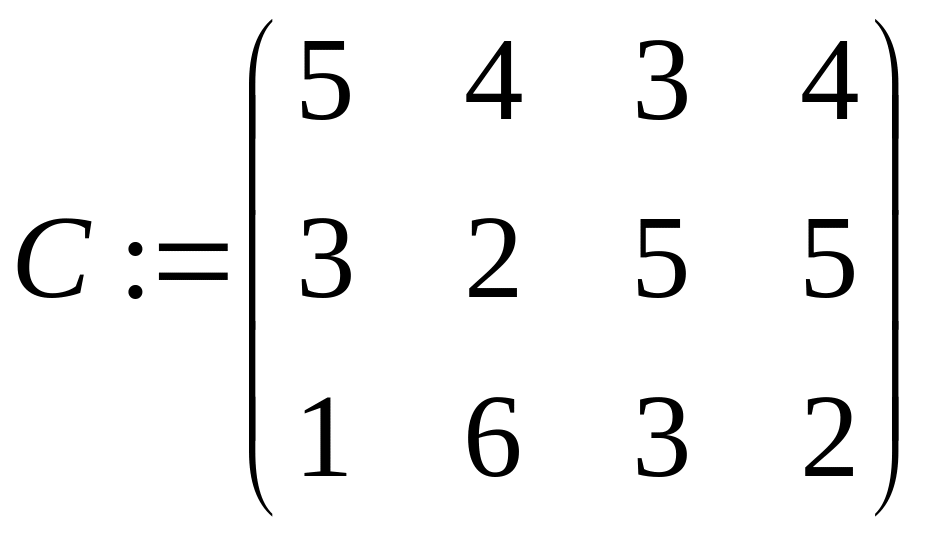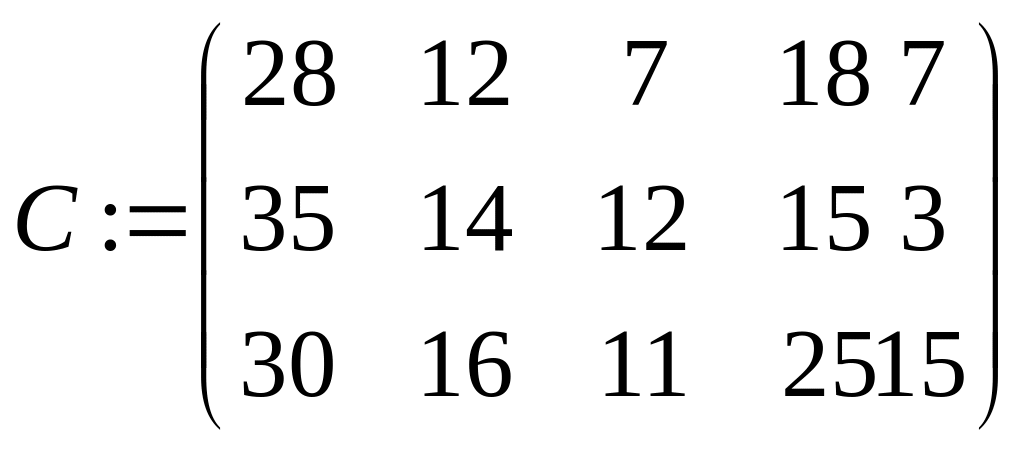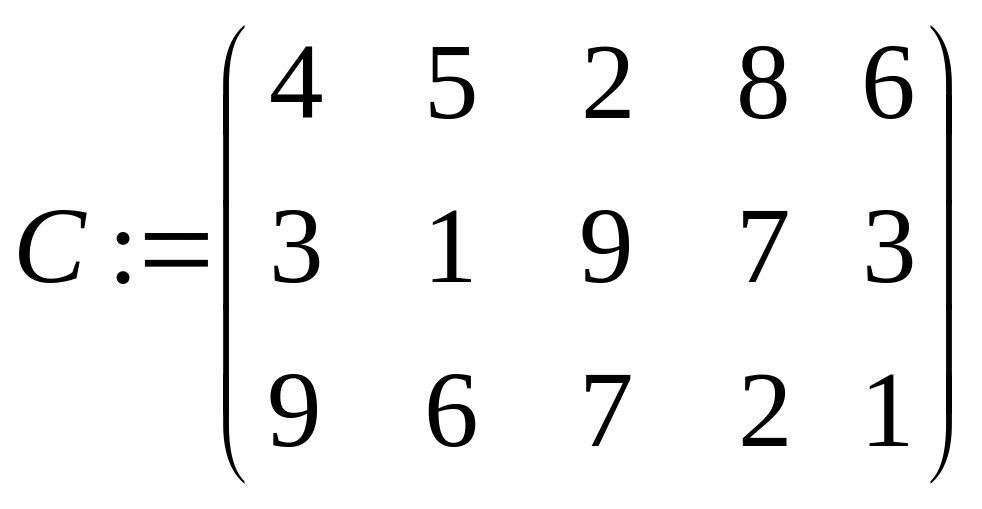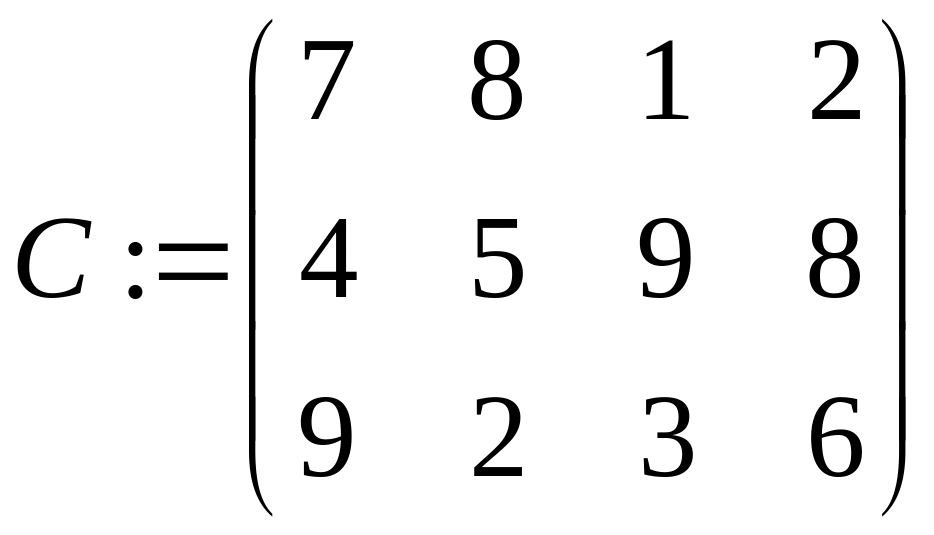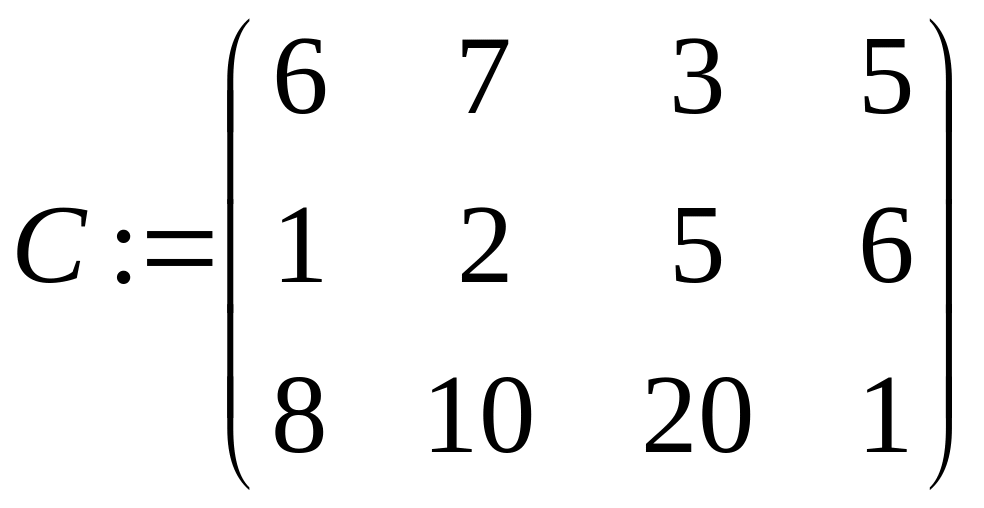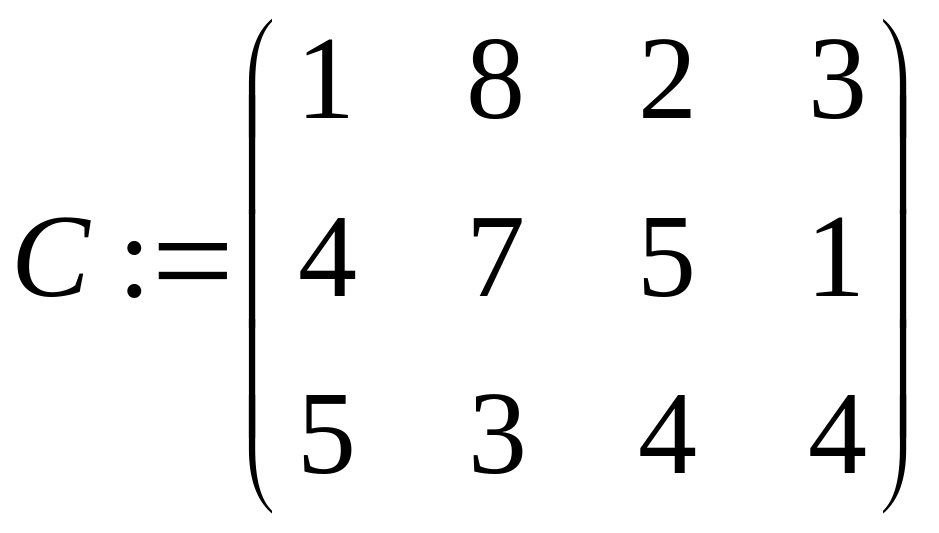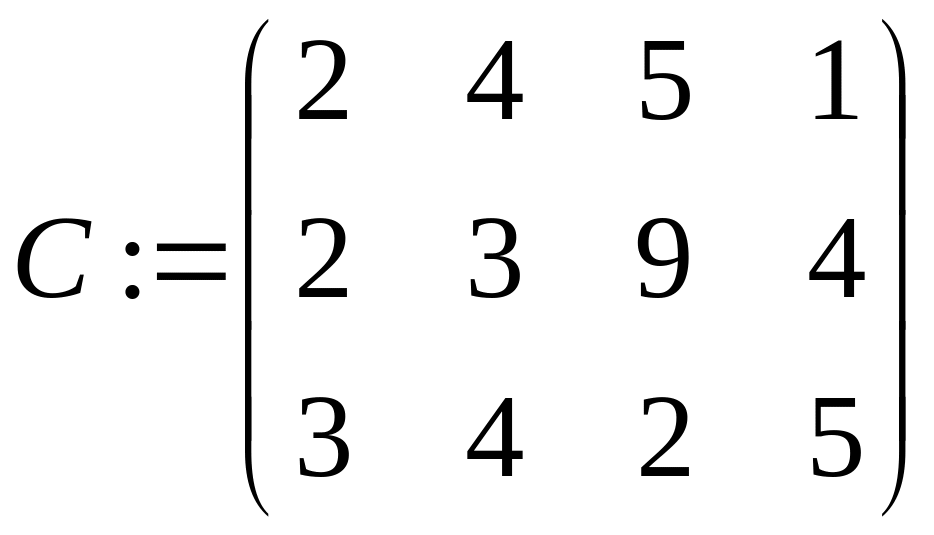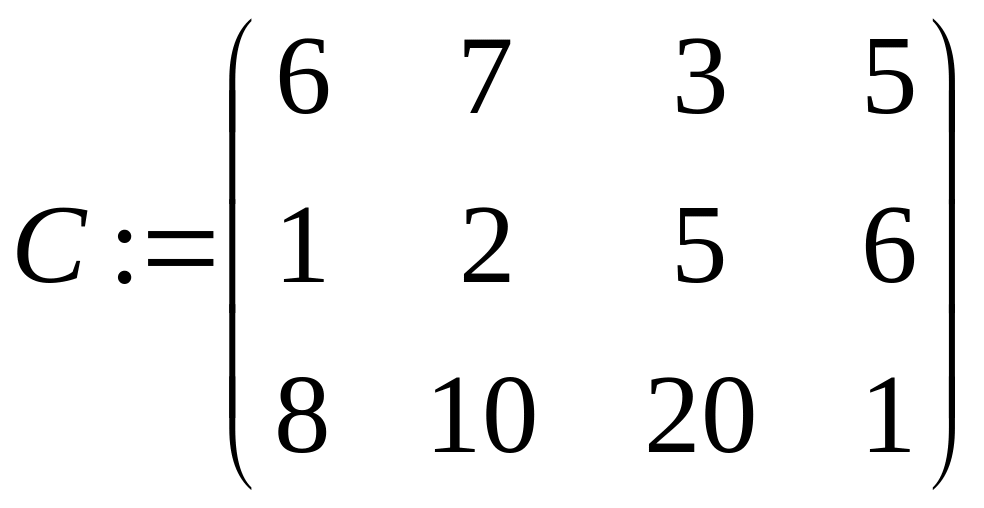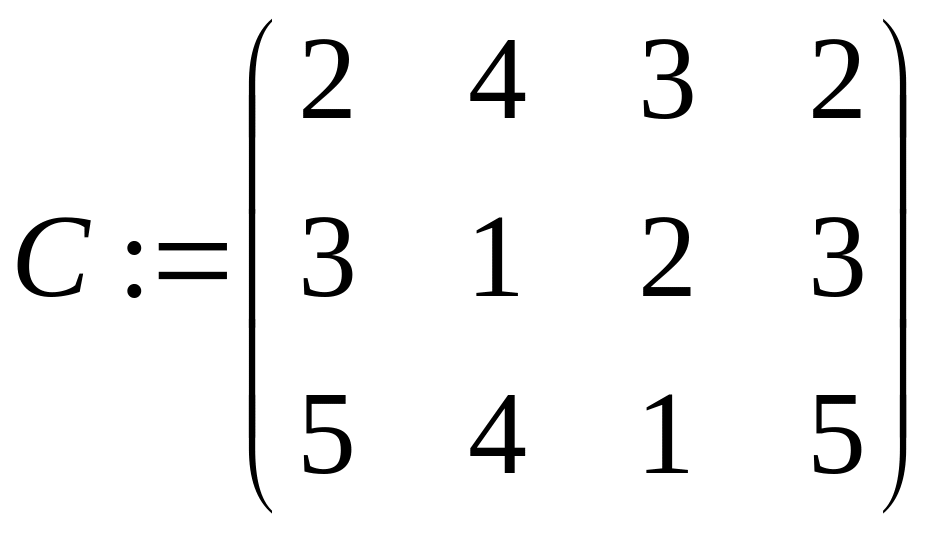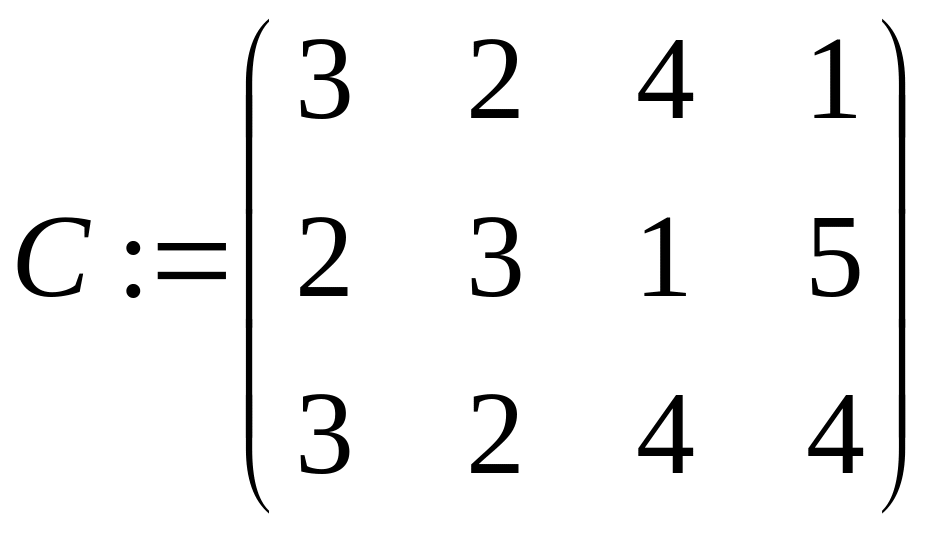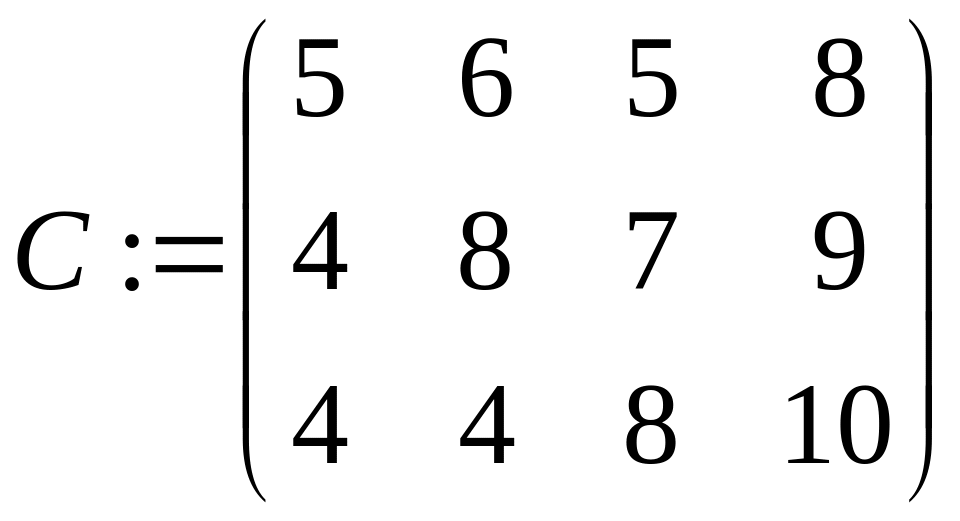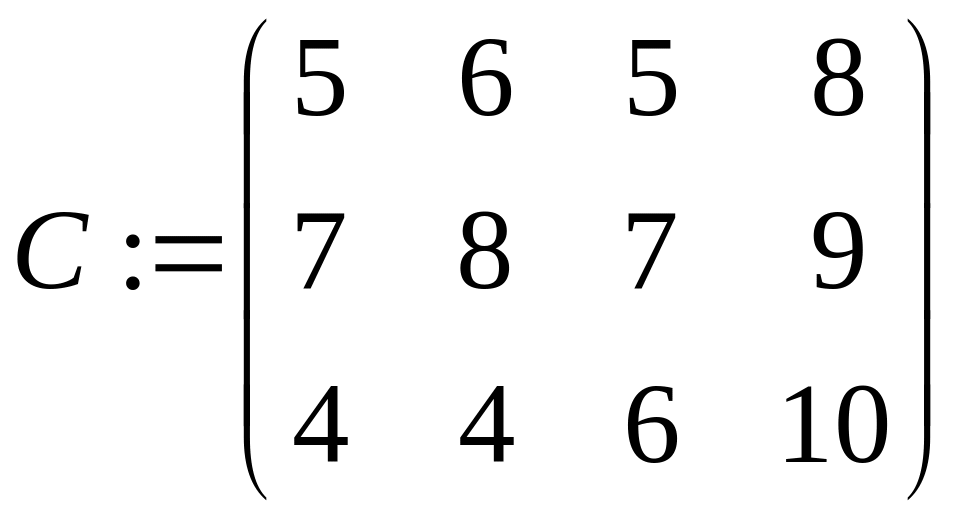Завдання №3

Нехай є m приймальників і n джерел інформації, з'єднаних між собою в мережу. Причому приймальники інформації між собою не зв'язані, а будь-який приймальник зв'язаний з будь-яким джерелом. Кожне i-е джерело i=1.. n володіє обсягом інформації a_i. Час передачі одиниці інформації від i-го джерела до j-го приймальника задається матрицею C=||c_ij||, i=1..n, j=1..m. Кожний j-й приймальник здатний прийняти обсяг інформації b_j. Потрібно скласти графік, що дозволить за мінімальний час одержати всю інформацію від усіх джерел.

1 a:={200, 270, 130} b:={120, 80, 240, 160}	11 a:={180, 60, 80} b:={120, 40, 80, 80}
2 a:={110, 190, 90} b:={80, 60, 170, 80}	12 a:={80, 140, 70} b:={80, 50, 50, 70, 40}
3 a:={160, 140, 60} b:={80, 80, 60, 140}	13 a:={155, 300, 220} b:={180, 120, 90, 105, 180}
4 a:={115, 175, 130} b:={70, 220, 40, 30, 60}	14 a:={140, 180, 160} b:={70, 60, 120, 120, 110}
5 a:={180, 350, 20} b:={110, 90, 120, 80, 150}	15 a:={160, 140, 170} b:={120, 50, 190, 110}
6 a:={100, 150, 50} b:={75, 80, 60, 85}	16 a:={25, 25, 50} b:={15, 15, 40, 30}
7 a:={45, 85, 20} b:={40, 30, 30, 50}	17 a:={40, 27, 23} b:={30, 25, 15, 20}

8 a:={50, 40, 20} b:={33, 22, 39, 16}	18 a:={15, 58, 35} b:={30, 23, 35, 20}
9 a:={35, 85, 60} b:={20, 60, 55, 45}	19 a:={90, 60, 90} b:={24, 40, 80, 96}
10 a:={16, 24, 30} b:={32, 14, 14, 10}	20 a:={16, 28, 30} b:={22, 18, 13, 21}

Задача вибору або задача про призначення

Транспортна задача і задача про призначення належать до одного різновиду розподільних задач, але методика їхнього розв`язку різна.

Класична постановка задачі:

1. У конструкторському бюро потрібно розробити проект машини, що складається із n вузлів. До їхньої розробки можна залучити n конструкторів. Відомий час, що витрачається кожним конструктором на розробку будь-якого вузла. Потрібно визначити, хто і який вузол машини повинен проектувати, щоб сумарний час проектування всієї машини був мінімальним.

2. У розподільній системі опрацювання даних у деякий момент часу є n ресурсів готових до виконання завдань. У систему надходить n завдань. Відома якість виконання завдань кожним ресурсом. Потрібно визначити кожному ресурсу своє завдання таким чином, щоб якість виконання всіх завдань була найкращою.

Математична модель має вигляд:

Функція цілі min (max)

Система граничних умов:

3. , 1 якщо i - й ресурс призначений на виконання j - й роботи; 0 - інакше.

Для розв`язку задачі про призначення застосовується угорський метод, що грунтується на двох теоремах.

Теорема 1: Якщо x_ij=X_ij мінімізує по всіх x_ij , таких, що x_ij0 і , те x_ij=X_ij мінімізує також функціонал , де при всіх i і j= 1,…,n...

Теорема 2 (Фробеніуса): Мінімальне число ліній, що покривають усі нулі матриці, дорівнює максимальному числу незалежних нулів у ній.

Незалежним нулем будемо називати єдиний вибраний нуль у рядку та стовпці, на перетині яких він знаходиться. Якщо крім вибранного незалежного нуля в рядку або стовпці присутні ще нулі, то їх далі необхідно вважати залежними. Фактично незалежний нуль на місці (i, j) є призначенням і – го зав- дання на виконання j-м ресурсом.

Фактично наведений метод розв`язку зводиться до перетворень рядків і стовпців за допомогою деяких констант доти, поки достатнє число коефіцієнтів Cij не обернеться в нуль, що дасть шуканий результат.

Нехай необхідно вирішити задачу про призначення 4 завдань на виконання 4 ресурсам, якщо задана матриця витрат часу на виконання кожного завдання кожним ресурсом: .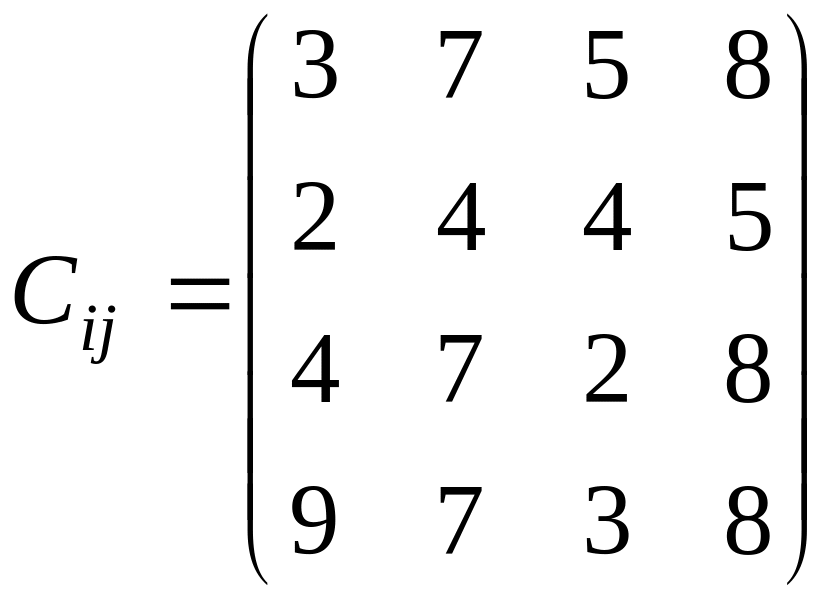

1. Приведемо матрицю до такого вигляду, щоб у кожному стовпці й кожному рядку знаходився хоча б один нуль. Для цього знайдемо в кожному рядку матриці мінімальний елемент і віднімемо його з усіх елементів відповідного рядка. Аналогічні перетворення виконаємо також з елементами стовпців.

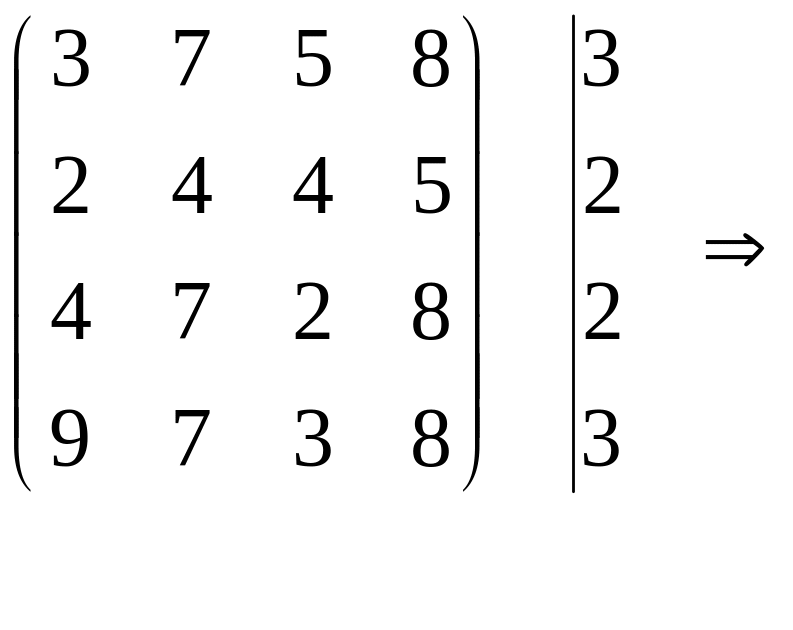
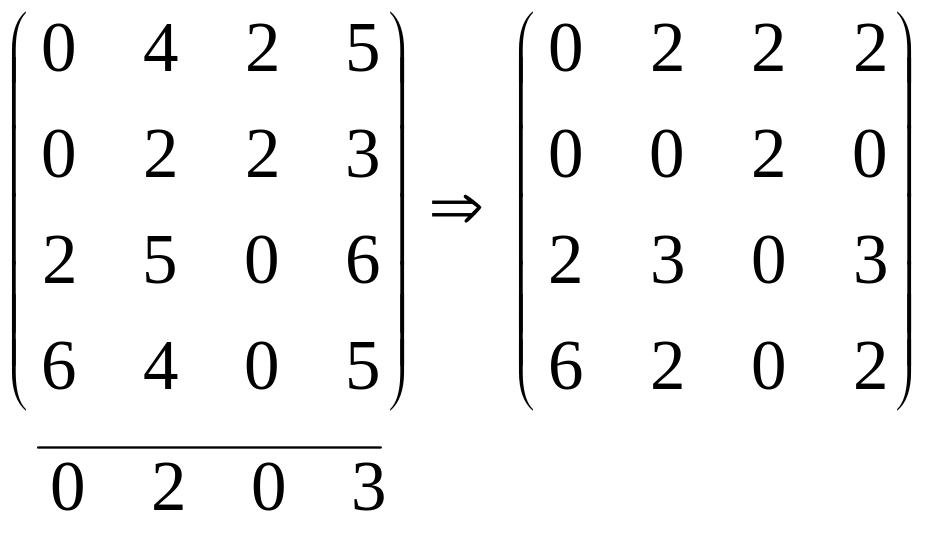
2. Якщо після першого кроку можливий вибір чотирьох незалежних нулів, тоді можна стверджувати, що задача вирішена. Незалежні нулі для зручності будемо позначати (*). При розставленні позначок найкраще вибирати рядок або стовпець, що містять найменшу кількість нулів. У цьому рядку (стовпці) вибираємо нуль, позначаємо його і викреслюємо інші нулі в рядку або стовпці, на перетинанні яких знаходиться вибраний (або незалежний) нуль. Позначки ставимо доти, поки в матриці існують вільні (непозначені або невикреслені) нулі.

У розглянутому прикладі не вдалося відразу ж одержати оптимальне рішення, отже, переходимо на виконання третього кроку.

3. Проведемо мінімальне число горизонтальних і вертикальних ліній, що перетинають, принаймні, один раз усі нулі . Для задач невеликої розмірності візуально легко нанести шукані лінії, для більш складних зручно використати насупний алгоритм:

1. Позначаємо всі рядки, що не містять незалежних нулів.

2. Позначаємо всі стовпці, що містять нуль хоча б в одному позначеному рядку.

3. Позначаємо всі рядки, що містять незалежні нулі в позначених стовпцях.

Кроки 2 і 3 виконуємо доти, поки можливо ставити позначки. Далі викреслюємо непозначені рядки і позначені стовпці.

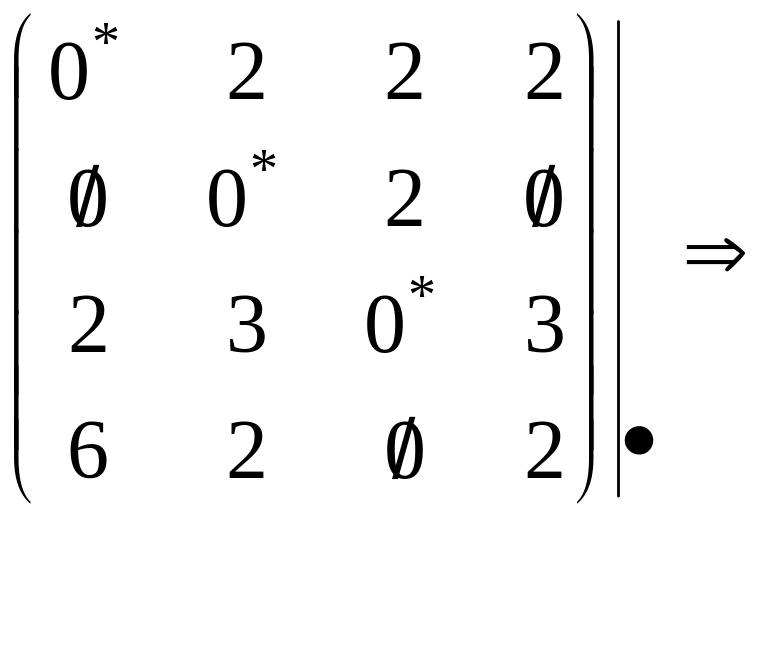
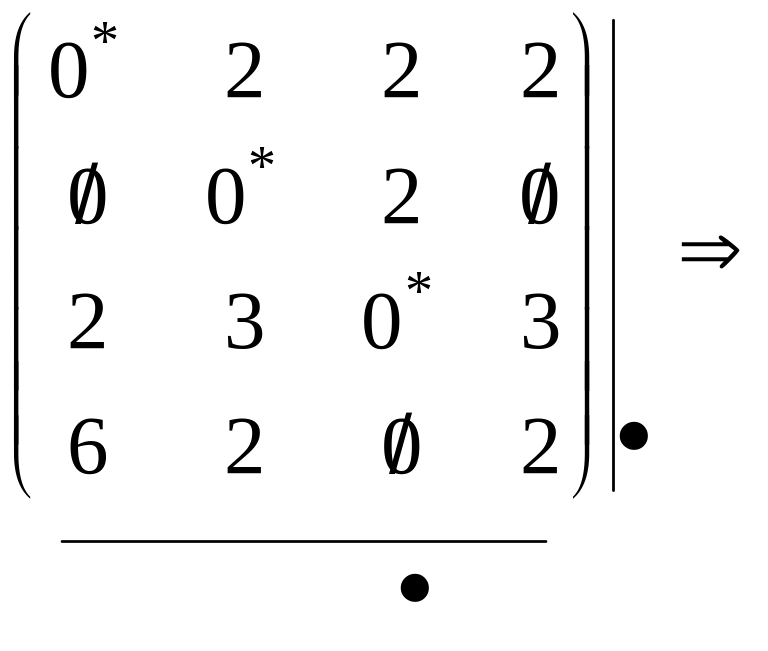
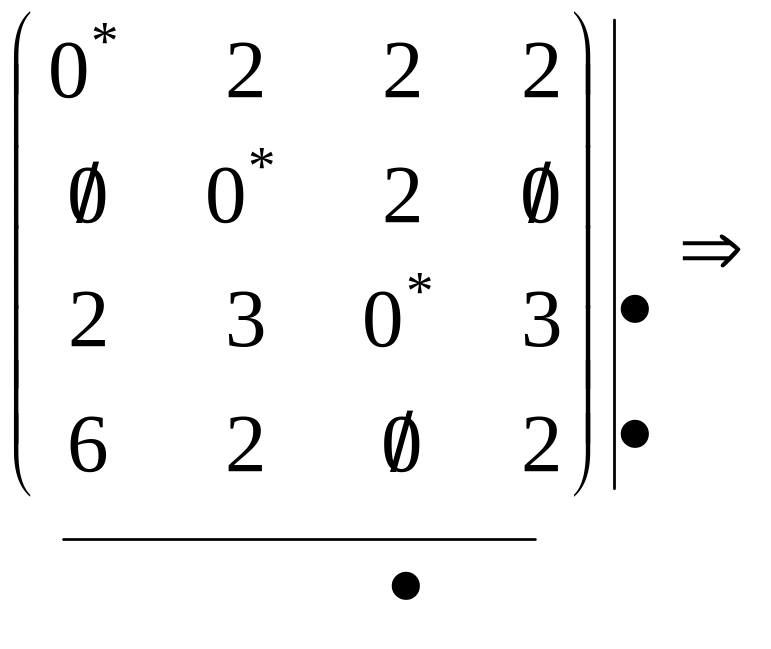
Якщо виявилося, що кількість ліній дорівнює n ,тоді необхідно повернутися на попередній крок (позначки нулів) і знову вибрати незалежні нулі. Такий варіант можливий, якщо при проставленні позначок 2 або більше нулів у рядку мали «однакове право» бути незалежними.

4. Серед елементів, через які не пройшла жодна з ліній, вибираємо найменший. Віднімаємо це число зі всіх елементів, через які не пройшла жодна лінія, і додаємо його до всіх елементів, через які проведені дві лінії.

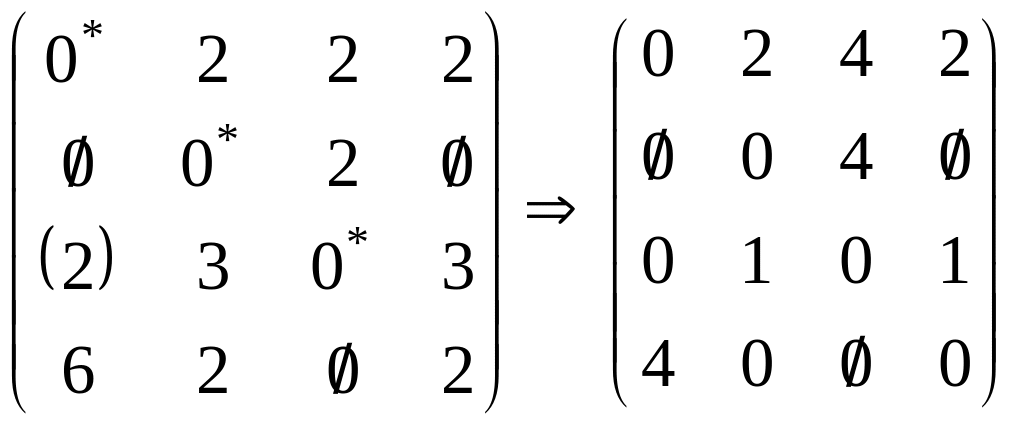
5. П 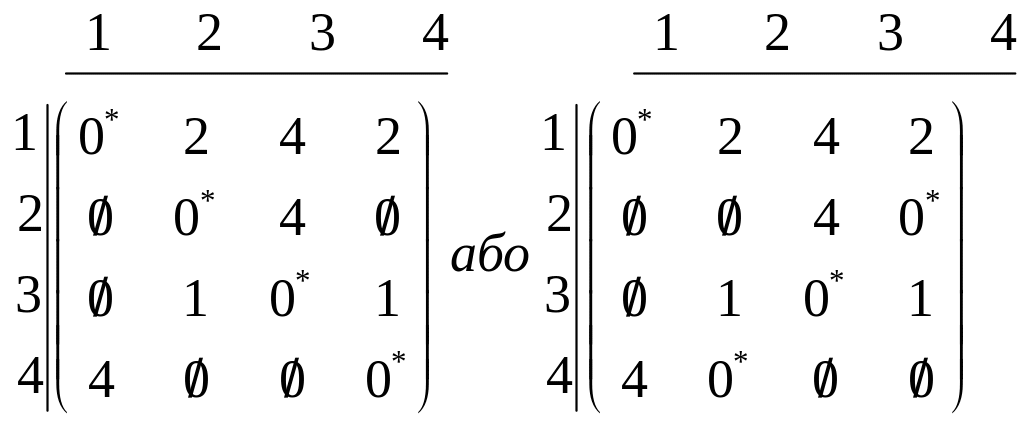овертаємося на крок вибору незалежних нулів. У розглянутому прикладі одержуємо відразу два оптимальних рішення:

1-е завдання  1-й ресурс

2-е завдання  2-й ресурс (або на 4-й ресурс)

3-е завдання  3-й ресурс

4-е завдання  4-й ресурс (або на 2-й ресурс)

У результаті такого призначення система виконає всі завдання за 17 умовних одиниць часу.

У тому випадку, якщо необхідно вирішити задачу отримання максимального значення функції цілі, можна скористатися наступною формулою переходу, що справедлива для будь-якої задачі лінійного і нелінійного програмування: min (L) = - max (-L) (тобто елементи матриці С домножити на (-1) ).