ЗМІСТ

Вступ……………… .......................... . .………………………… ..........................…....4

Вибір варіанта завдання…………………………………………………………….…..4

Частина 1. Лінійне і цілочисельне програмування …………………………........5

Геометрична інтерпретація задач лінійного програмування…………………….…..5

Завдання №1……………………………………………………………………………..7

Симплексний метод вирішення загальної задачі лінійного програмування………..9

Завдання №2 …………………………………………………………………………..12

Транспортна задача……………………………………………………………………14

Завдання №3.…………………………………………………………..................…….19

Задача вибору або задача про призначення………………………………………….21

Завдання №4 ………… . .……………………………………………………………...25

Частина 2. Нелінійне програмування……………………………………………..26

Методи одновимірної пошукової оптимізації……………………………………….26

Завдання №5 ……….. .....……………………………………………………….....….33

Нелінійна багатовимірна безумовна оптимізація…………………………………...34

Завдання №6 .....……………………………………………………….....…………….43

Нелінійна багатовимірна умовна оптимізація……………………………………….45

Завдання №7 ..…………………………………………………………...……………..46

Частина 3. Теорія розкладу. Задача Джонсона …………………………………..47

Завдання №8 .……………………………………………………………..……….…...50

ЛІТЕРАТУРА …...………………………………………………………………......…53

ВСТУП

Даний навчально-методичний посібник рекомендується студентам напряму підготовки 7.091501- “Комп`ютерні системи та мережі” при виконанні семестрової роботи з дисципліни “Методи оптимізації”. Передбачається, що студенти вивчили дисципліни “Вища математика”, “Дискретна математика” і “Теорія імовірностей і математична статистика”.

В методичному посібнику наведено перелік усіх завдань семестрової роботи, що складається із семи завдань. Перед кожним завданням подано теоретичний матеріал, необхідний для рішення поставленої задачі, тому посібник можна використати для самостійної підготовки.

Отримані знання будуть використані при вивченні дисциплін “Організація обчислювальних процесів”, “Програмування” та ін.

Вибір варіанта завдання

Варіант завдання студенти вибирають із таблиці за двома останніми цифрами шифру в заліковій книжці.

Передостання цифра шифру студента		Остання цифра шифру студента
		0	1	2	3	4	5	6	7	8	9
	0	20	1	2	3	4	5	6	7	8	9
	1	1 0	11	12	13	14	15	16	17	18	19
	2	20	1	2	3	4	5	6	7	8	9
	3	10	11	12	13	14	15	16	17	18	19
	4	20	1	2	3	4	5	6	7	8	9
	5	10	11	12	13	14	15	16	17	18	19
	6	20	1	2	3	4	5	6	7	8	9
	7	10	11	12	13	14	15	16	17	18	19
	8	20	1	2	3	4	5	6	7	8	9
	9	10	11	12	13	14	15	16	17	18	19

Частина 1. Лінійне і цілочисельне програмування геометрична інтепретація задач лінійного програмування

Множина припустимих рішень (багатогранник рішень) задача лінійного програмування являє собою опуклий багатогранник ( або опуклу багатогранну область ), а оптимальне рішення задачі знаходиться, принаймні, в одній із кутових точок багатогранника рішень.

Розглянемо задачу в стандартній формі з двома змінними:

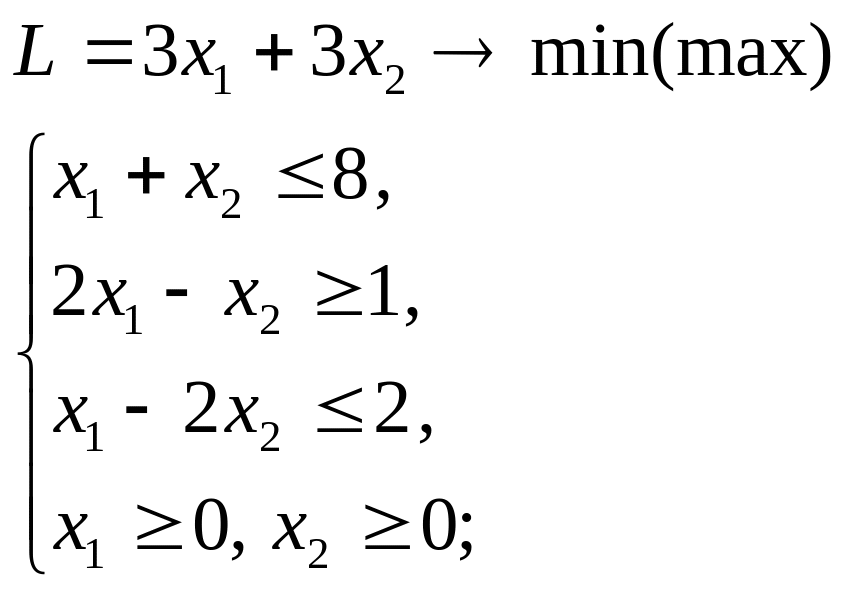
До такої форми може бути зведена і канонічна задача ( з обмеженнями у виді рівнянь), коли число змінних n більше числа рівнянь m на 2, тобто n - m = 2.

Множина рішень кожної нерівності із системи обмежень є напівплощина. Побудуємо границі напівплощин - прямі

.

Для визначення розміщення на малюнку шуканих напівплощин (верхніх або нижніх) рекомендується задати довільну контрольну точку, що не лежить на межах побудованих прямих (наприклад, точка з координатами (0,0)). Якщо нерівність виконується в контрольній точці, то вона виконується у всіх точках напівплощини, що містить контрольну точку, і не виконується у всіх точках іншої напівплощини. Геометричним зображенням системи обмежень є багатогранник ABCD (мал.1).

Нанесемо на малюнку лінію рівня лінійної функції L: 3x1+3x2=9 (функцію цілі прирівняли до довільної константи ). Важлива властивість лінії рівня полягає в тому, що при паралельному зсуві лінії в одну сторону значення функції цілі тільки зростає, а при зсуві в іншу сторону - тільки убуває. Отже, при зсуві лінії рівня вбік зростання функції цілі можна визначити точку максимуму - це точка, у якому лінія рівня і багатогранник рішень стикнуться востаннє. Аналогічним способом можна визначити точку мінімуму. У розглянутому прикладі точкою мінімуму є точка D, а точкою максимуму буде будь-яка точка, що належить відрізку АВ (лінії рівня паралельні граничнії прямії другої напівплощини ). Визначимо ці точки.

Варто зауважити, що точка D знаходиться на перетині двох прямих : 2x₁-x₂=1 і x₂=0.

Тобто точка мінімуму має координати (0.5; 0). Аналогічно визначаємо координати точки А (3 ; 5) і точки В (2 ; 6).

У результаті одержуємо:

• найменше значення L_min=1.5 функція цілі набуває в точці D (0.5 ;0);

• найбільше значення L_max=24 функція цілі набуває в будь-якій точці відрізка АВ.