Завдання №1

Використовуючи геометричну інтепретацію задач лінійного програмування, визначити екстремальні значення функції цілі при заданій системі обмежень (або переконатись в її нерозв'язності).

1. L=3x1+4x2min(max)	11 L=5x1+4x2min(max)
2 L=-x1+4x2min(max)	12 L=5x1+x2min(max)
3 L=-x1+5x2min(max)	13 L=x1-5x2min(max)
4 L=x1+2x2min(max)	14 L=x1-x2min(max)
5 L=9x1+2x2min(max)	15 L=x1+2x2min(max)
6 L=10x1+11x2min(max)	16 L=x1+3x2min(max)
7 L=5x1+3x2min(max)	17 L=5x1-3x2min(max)
8 L=-x1+x2min(max)	18 L=7x1-2x2min(max)
9 L=5x1+7x2min(max)	19 L=3x1-3x2min(max)
L=4x1+3x2min(max)	20 L=2x1+x2min(max)

Симплексний метод вирішення загальної задачі лінійного програмування

Розглянемо задачу лінійного програмування в загальному вигляді:

граничні умови

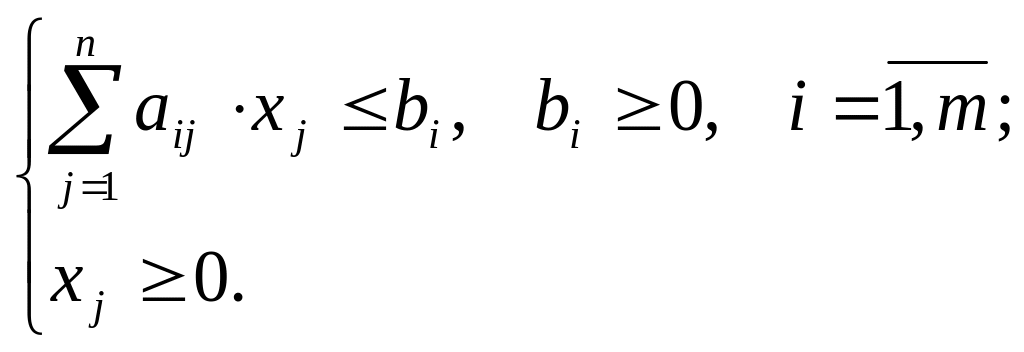
Довільну задачу лінійного програмування можна вирішити за допомогою універсального математичного методу, який отримав назву симплексного методу. Але для його використання необхідно привести систему граничних умов поставленої задачі до канонічного вигляду, добавивши додаткові змінні . В результаті отримали розширену задачу, еквіваленту вихідній задачі. У функцію цілі додаткові змінні вводяться з нульовими коефіцієнтами: .

Якщо кожна гранична умова системи обмежень має змінну, що входить у ліву частину умови з коефіцієнтом, рівним 1, а в усі інші – рівним 0, (при не негативних вільних елементах) то система подана у бажаному вигляді. Такі змінні можна назвати базисними. Щоб отримати опорне рішення, необхідно всі змінні, крім базисних, прирівняти до нуля, а базисним надати значення правих частин відповідних рівнянь. Змінні, що набули значення нуля, називаються вільними.

Складаємо симплексну таблицю по принципу:

Xbj	X1	X2	…	Xn	п.ч. (bj)
Базисні змінні	Коефіцієнти a1j при X1 в умовах	Коефіцієнти a2j при X2 в умовах	. . .	Коефіцієнти anj при Xn в умовах	Стовпець вільних членів в умовах
L	- C1	- C2	…	- Cn	0

Далі виконуємо симплексні перетворення:

• обчислення проводяться доти доти, поки в оцінному рядку не будуть знаходитись невід`ємні оцінки для задачі максимізації або з недодатні оцінки для задачі мінімізації;

• вибираємо стовпцем, для якого оцінка буде найбільшим за модулем негативним (позитивним) числом, якщо вирішується задача максимізації (мінімізації) – цей стовпець буде вирішаючим;

• у вирішаючому стовпці , вибираємо позитивний елемент, що відповідає найменьшому позитивному відношенню елементів вільного стовпця до відносних елементів вирішаючого стовпця;

• рядок, у якому знаходиться вибраний елемент вирішаючого стовпця, називається вирішаючим;

• далі будуємо нову симплексну таблицю на основі елементів вихідної таблиці :

1. Елементи вирішаючого рядка діляться на вирішаючий елемент. Нехай вирішаючим буде r-й рядок.

2. Елементи вирішаючого стовпця, всі, крім вирішаючого, діляться на вірішаючий елемент з протилежним знаком, а вирішаючий дорівнює своєму оберненому значенню. Нехай вирішаючим буде s-й стовпець.

3. Елементи, що залишилися, у таблиці обчислюються за правилом прямокутника, завжди починаючи з вирішаючого елемента:

a_ij-шуканий елемент, a_rs- вирішаючий елемент

a_{i j} a_{i s}

a_{r j} a_{r s}

Тобто, у вихідній таблиці виділяємо прямокутник, вершинами якого служать наступні елементи: вирішаючий, шуканий, а також елементи з вирішаючого рядка і стовпця. Діагональ, що містить вирішаючий і шуканий елементи, назвемо головною, а другу - побічною. З твору кутових елементів головної діагоналі відраховується твір кутових елементів побічної діагоналі й отримане число поділяють на вирішаючий елемент. Це - правило прямокутника.

Розглянемо крок симплексних перетворень на прикладі:

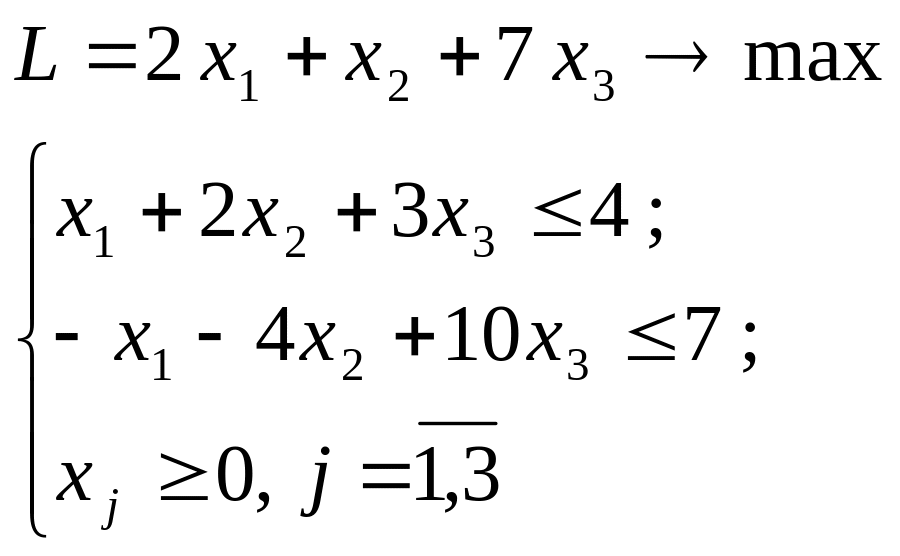в канонічному виді

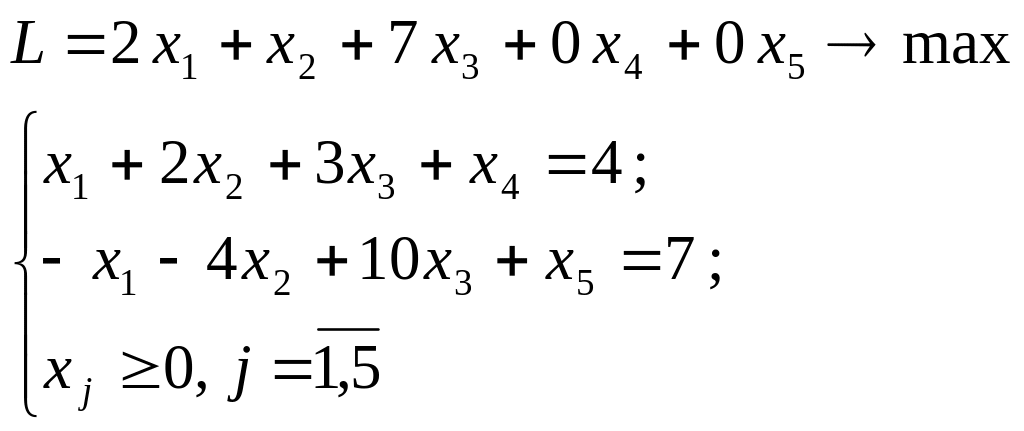
Xb	X1	X2	X3	bj	Qj
X4	1	2	3	4	4/3
X5	-1	-4	10	7	7/10

L	-2	-1		-7	0
Xb	X1		X2	X5	bj
X4	13/10		32/10	-3/10	19/10
X3	-1/10		-4/10	1/10	7/10
L	-27/10		-38/10	7/10	49/10

Xb	X1		X4	X5	bj	Qj
X2	13/32		10/32	-3/32	19/32	19/13
X3	1/16		2/16	1/16	15/16	15
L	-37/32	19/32		11/32	229/32
Xb	X2		X4	X5	bj
X1	32/13		10/13	-3/13	19/13
X3	-2/13		1/13	1/13	11/13
L	37/13	27/13		1/13	115/13

Отримали оптимальне рішення .