- •1. Линейная алгебра и аналитическая геометрия
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
- •1. Линейная алгебра и аналитическая геометрия Задача 1. Дана система линейных неоднородных алгебраических уравнений
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
2. Дифференциальное и интегральное исчисления
Задача 3. Найти указанные пределы:
а)
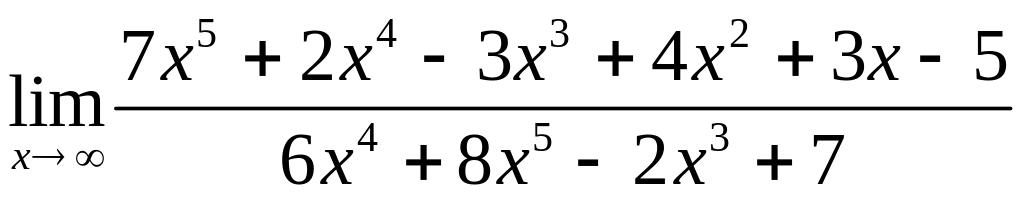 ;
б)
;
б)
 ;
;
в)
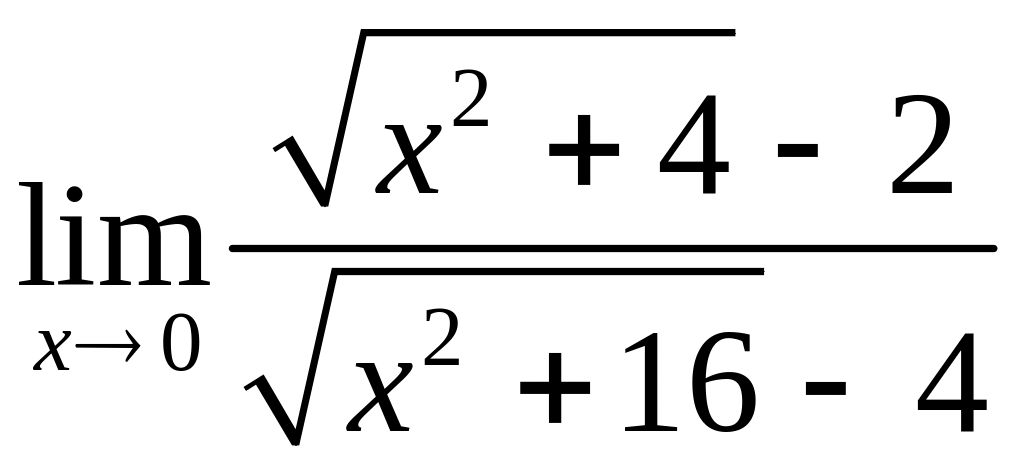 ;
г)
;
г)
![]() ;
д)
;
д)
 .
.
Решение.
а)
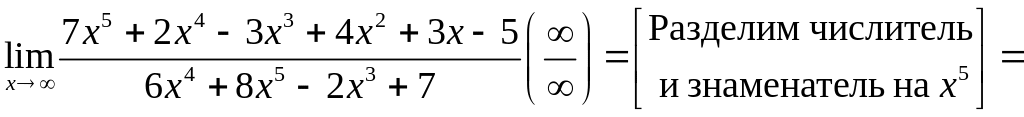

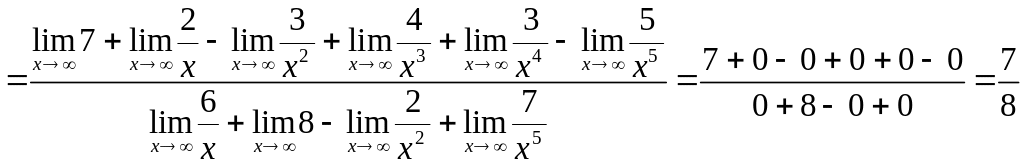 ;
;
б)

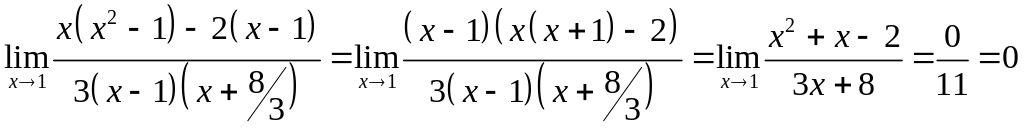 ;
;
в)
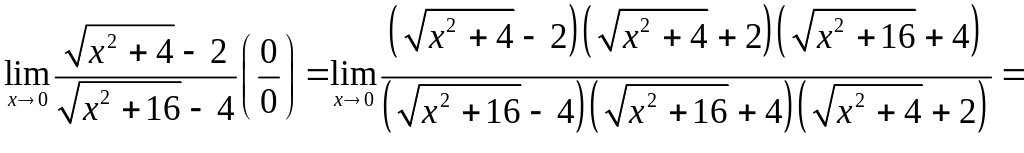
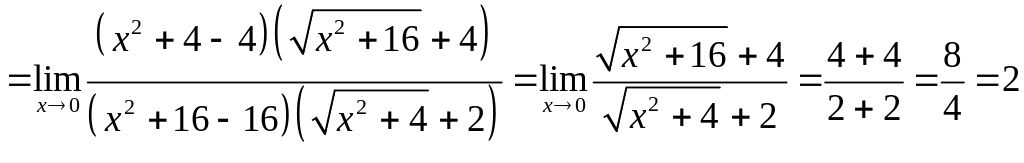 ;
;
г)

![]()
![]() ;
;
д)
Здесь используем 2-й замечательный
предел
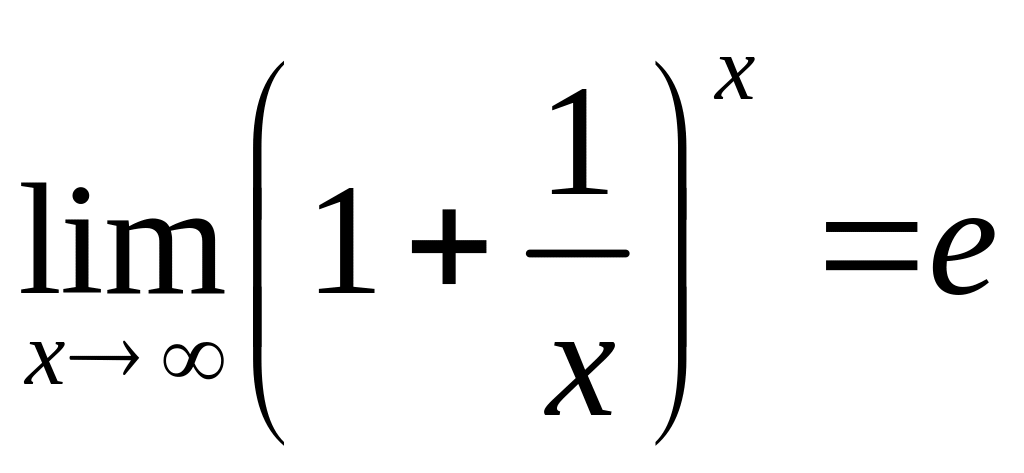 .
Получим
.
Получим
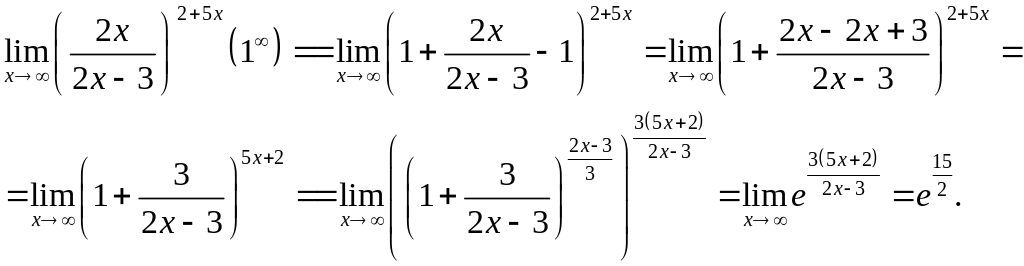
Задача
4.
Продифференцировать
функции: а)
![]() ;
;
б)
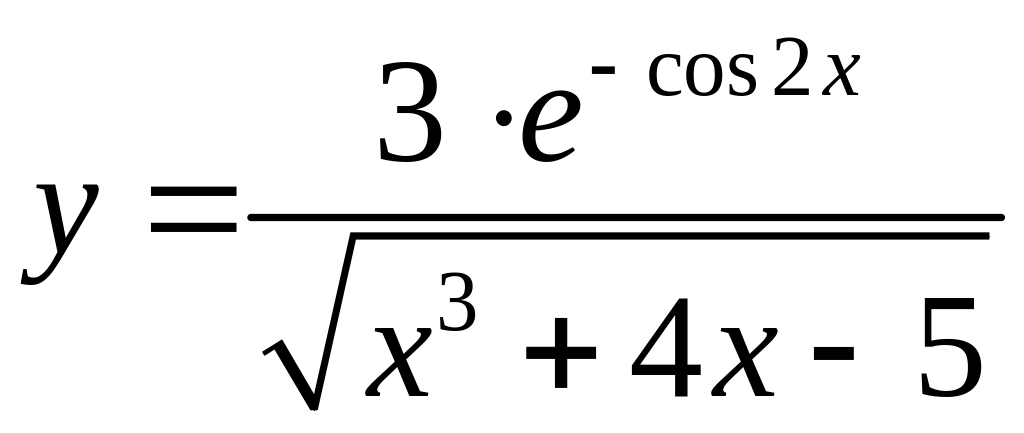 ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
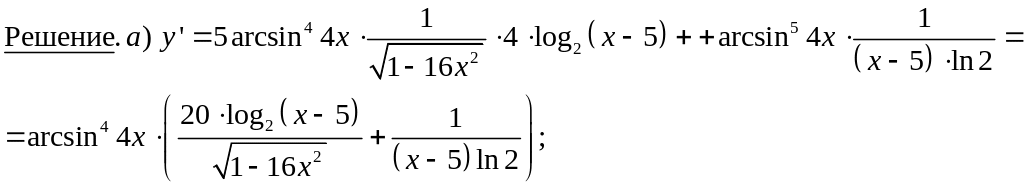
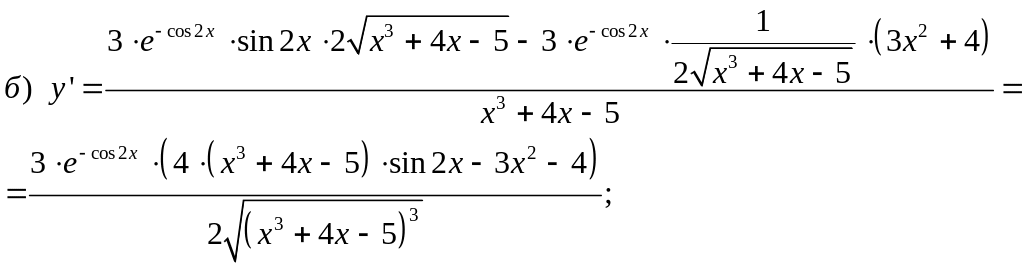
в) Прологарифмируем данную функцию:
![]() .
.
Тогда
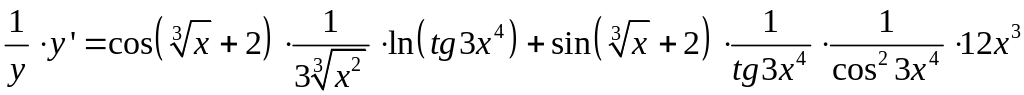 .
.
Выразим
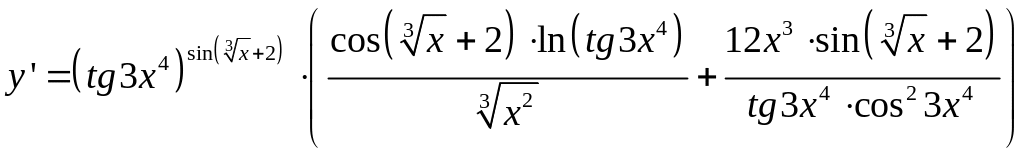 ;
;
г) Продифференцируем, имеем равенство:
![]() Выразим
Выразим
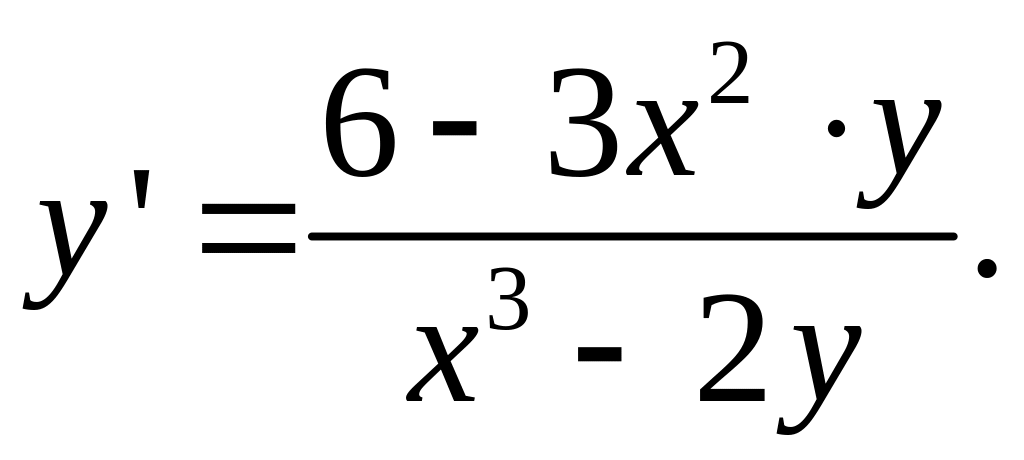
Задача 5. Найти наименьшее и наибольшее значение функции
![]() на отрезке
на отрезке
![]() .
.
Решение.
Функция
определена на этом отрезке. Найдем
критические точки:
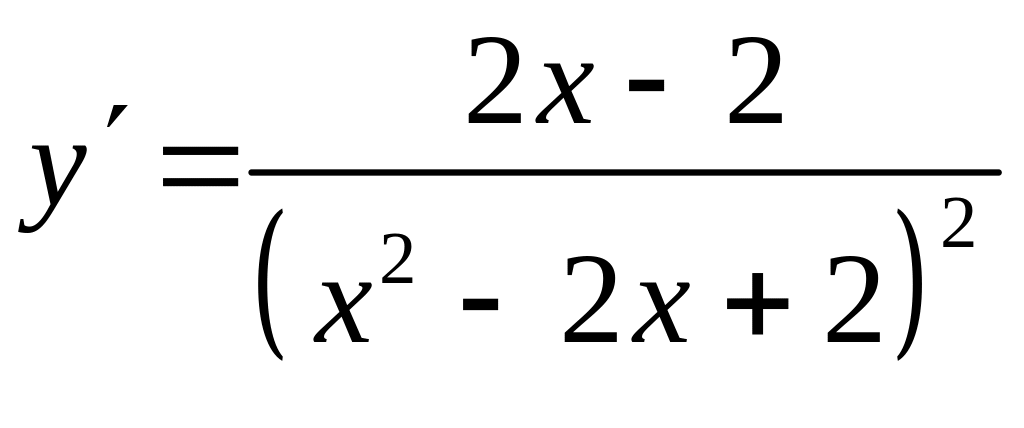 .
Если
.
Если
![]() ,
то
,
то
![]() .
Найденная точка принадлежит отрезку
.
.
Найденная точка принадлежит отрезку
.
![]() существует для всех
существует для всех
![]() ,
т.к.
,
т.к.
![]() для всех
.
Найдем значения функции при
для всех
.
Найдем значения функции при
![]() и
и
![]() :
:
![]() .
.
Следовательно,
наименьшего значения данная функция
достигает в точке
![]() :
:
![]() ,
а наибольшего – в точке
,
а наибольшего – в точке
![]() .
.
Задача
6. Исследовать
функцию
![]() и построить её график.
и построить её график.
Решение. Общая схема построения графика функции:
находим область определения функции;
исследуем функцию на периодичность, четность или нечетность;
исследуем функцию на монотонность и экстремум;
находим промежутки выпуклости и точки перегиба;
отыскиваем асимптоты графика функции;
для уточнения хода графика функции находим точки пересечения его с осями координат;
строим график функции.
В нашем случае имеем:
1. Областью
определения
![]() функции является множество
функции является множество
![]() .
.
Функция нечетная, т.к. область ее определения симметрична относительно начала координат и выполнено условие
 .
Функция непериодическая.
.
Функция непериодическая.
3. Находим
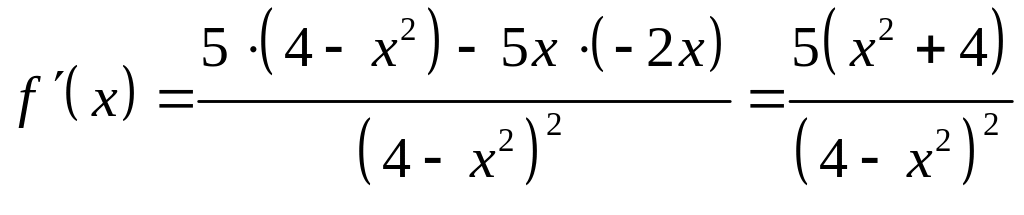 .
Видим, что
.
Видим, что
![]() для всех
для всех
![]() и
и
![]() не существует, если
не существует, если
![]() .
Эти
.
Эти
точки разбивают область определения функции на промежутки
![]() .
Исследуем знак производной
на этих
.
Исследуем знак производной
на этих
промежутках. Результаты заносим в таблицу
|
|
|
|
2 |
|
|
+ |
|
+ |
|
+ |
|
возрастает |
|
возрастает |
|
возрастает |
Из таблицы видно, что функция всюду возрастает на и точки локального минимума и максимума не имеет.
4. Находим
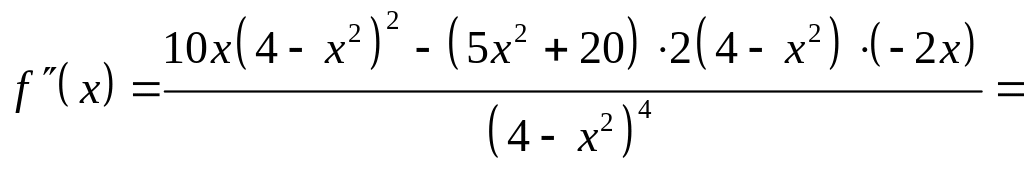
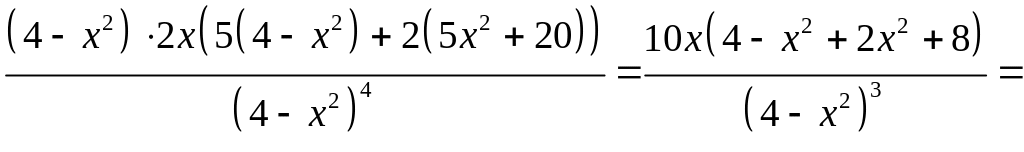
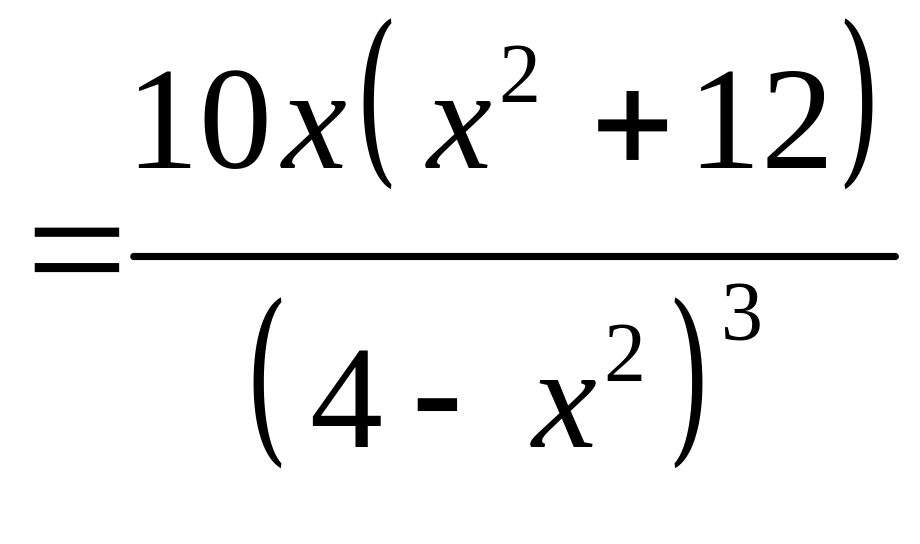 .
Точками возможного перегиба являются
точки
.
Точками возможного перегиба являются
точки
![]() .
Они разбивают область определения
функции на
.
Они разбивают область определения
функции на
промежутки
![]() .
Исследуем знак
.
Исследуем знак
![]() на этих
на этих
промежутках. Результаты исследования заносим в таблицу
|
|
|
|
0 |
|
2 |
|
|
+ |
|
– |
0 |
+ |
|
– |
|
выпукла вниз |
|
выпукла вверх |
0 перегиб |
выпукла вниз |
|
выпукла вверх |
5. Вертикальными
асимптотами являются
![]() и
и
![]() ,
причем
,
причем
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ищем
наклонную асимптоту
![]() .
Так как
.
Так как
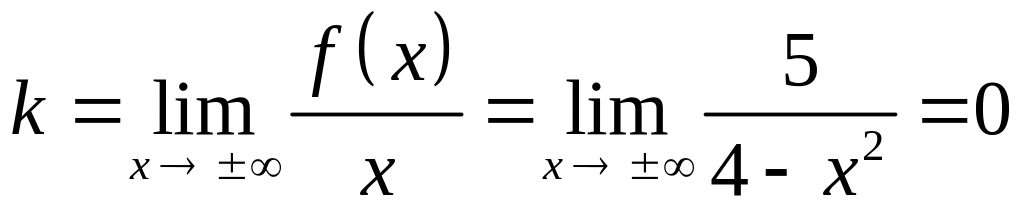 ,
,
![]() ,
то
,
то
![]() – горизонтальная асимптота.
– горизонтальная асимптота.
6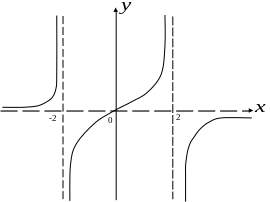 .
Находим точки пересечения графика с
осями координат. Это точка
.
Находим точки пересечения графика с
осями координат. Это точка
![]() .
.
7. Строим график функции
Задача 7. Найти следующие интегралы.
а)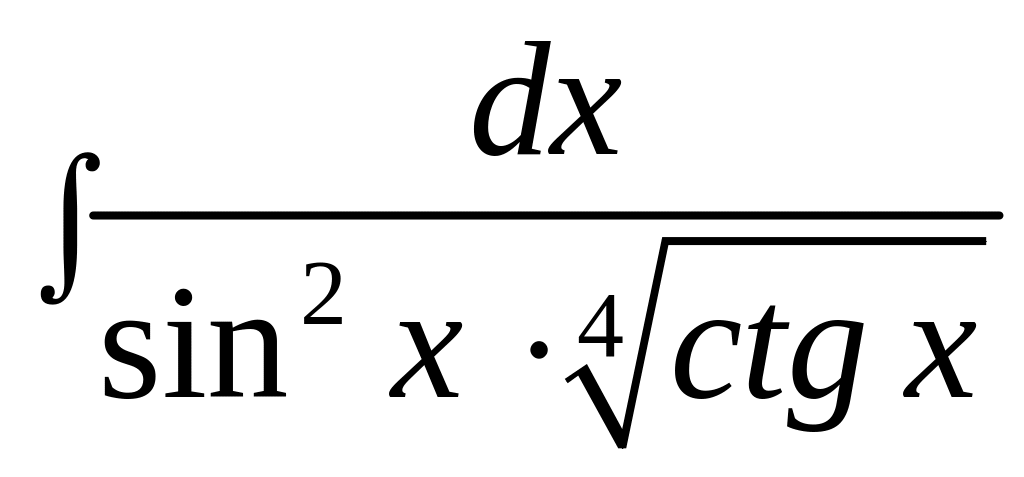 ;
б)
;
в)
;
б)
;
в)
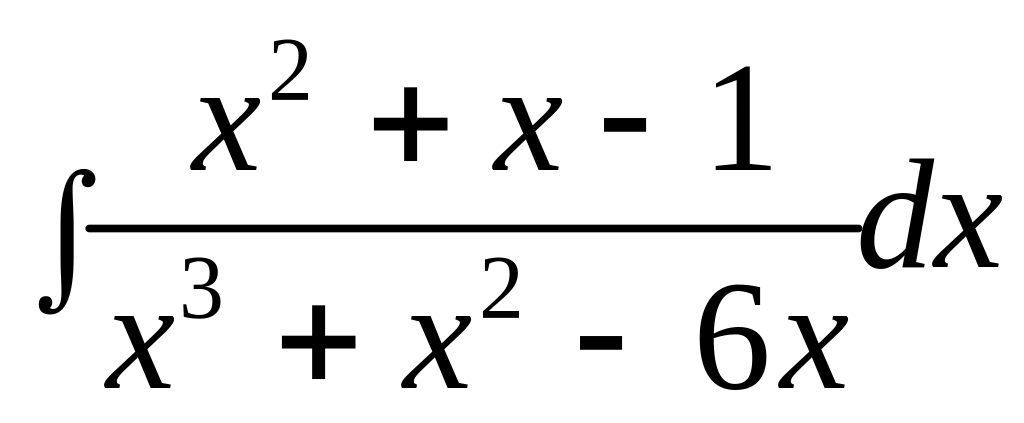 ;
;
г)
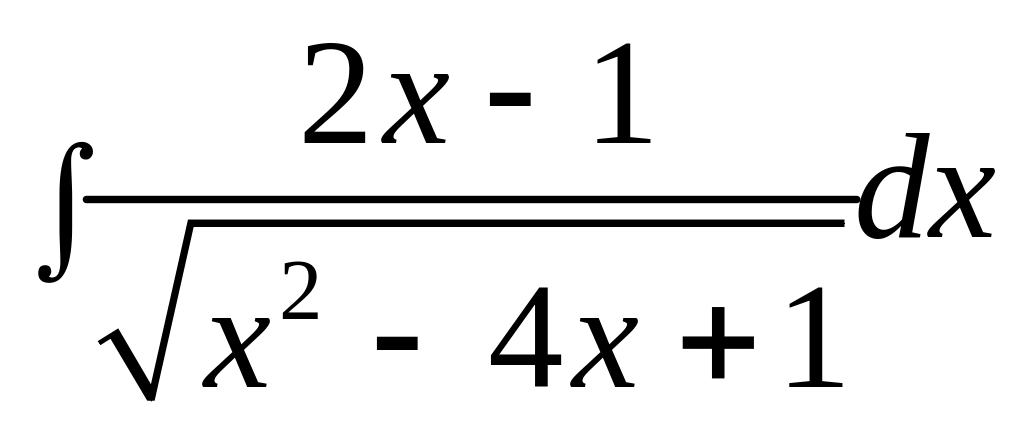 ;
д)
;
д)
 ;
е)
.
;
е)
.
Результат интеграла а) проверить дифференцированием.
Решение
. а)
 .
Произведем замену переменной
.
Произведем замену переменной
![]() .
Дифференцируем это равенство
.
Дифференцируем это равенство
![]() или
или
![]() ,
тогда
,
тогда

Проверка:
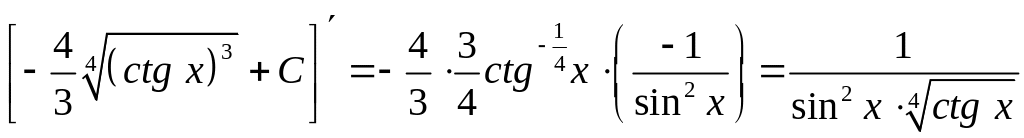 ;
;
б) .
Воспользуемся формулой интегрирования по частям:
![]() .
Положим
.
Положим
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
.
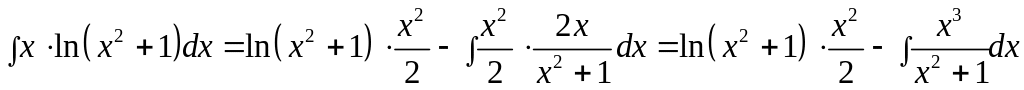 .
.
Отдельно
вычислим
 .
Разделим
.
Разделим
![]() на
на
![]() по правилу деления
по правилу деления
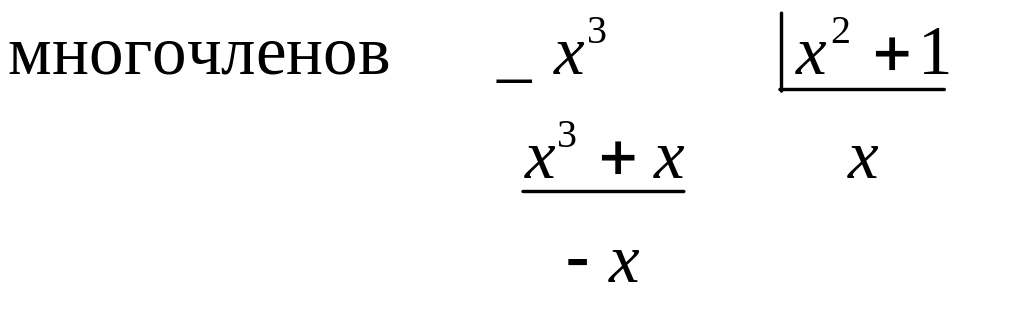 Тогда
Тогда
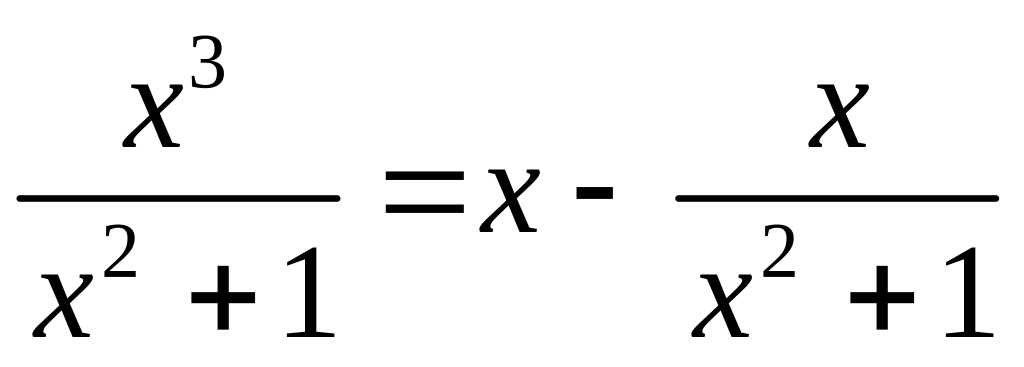 .
.
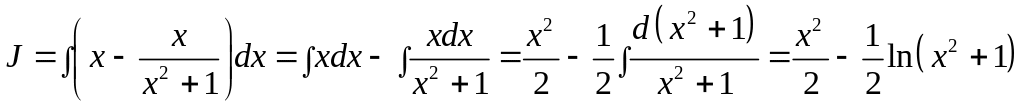 .
.
Исходный интеграл равен
![]() в)
в)
 .
.
Разложим правильную рациональную дробь (степень числителя «2» меньше степени знаменателя «3») на сумму простейших дробей:
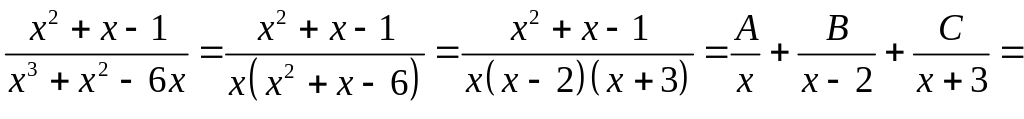

Приравниваем числители первой и последней дробей
![]()
Сгруппируем члены с одинаковыми степенями:
![]() .
.
Сравнивая коэффициенты при одинаковых степенях , получаем систему уравнений:
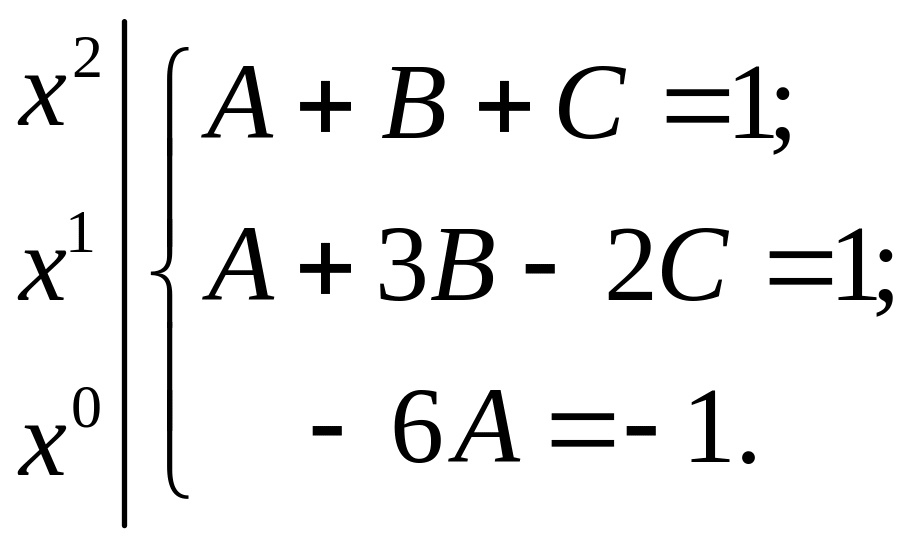

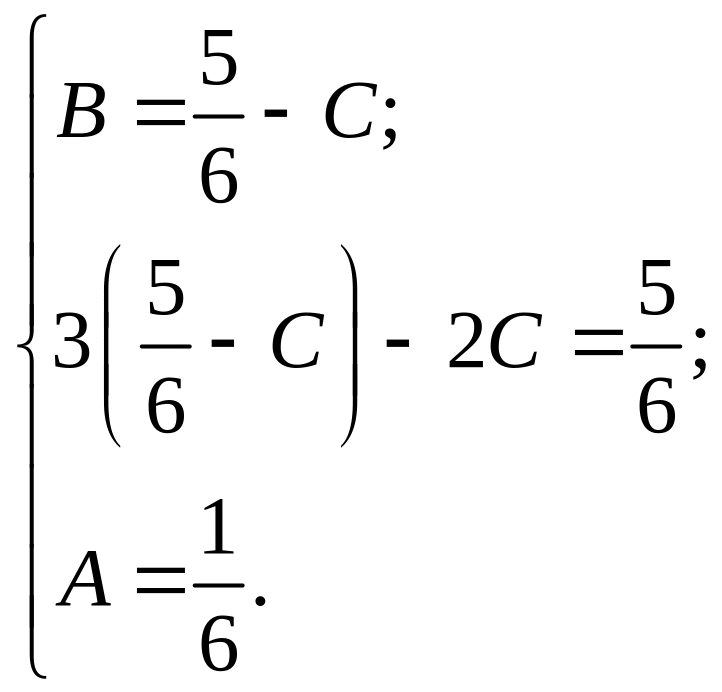
![]()
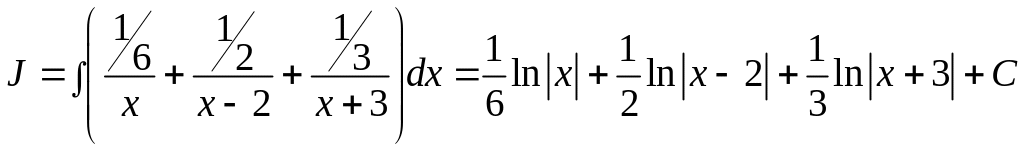 ;
;
г)
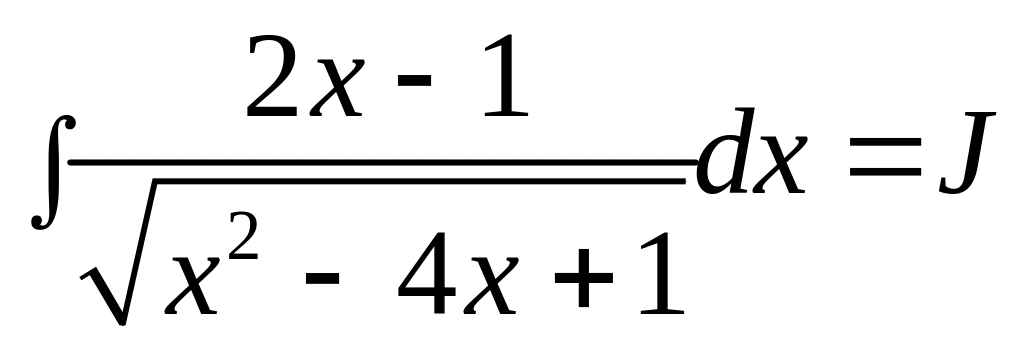 .
Выделим полный квадрат в выражении,
стоящем под корнем
.
Выделим полный квадрат в выражении,
стоящем под корнем
![]() и сделаем замену переменной
и сделаем замену переменной
![]() .
.
Тогда
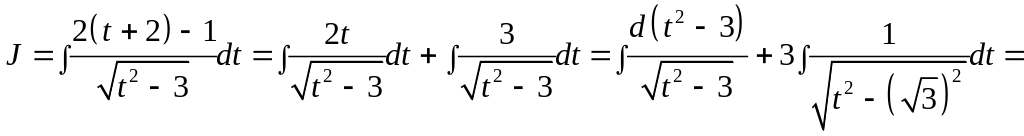
![]()
![]() ;
;
д)
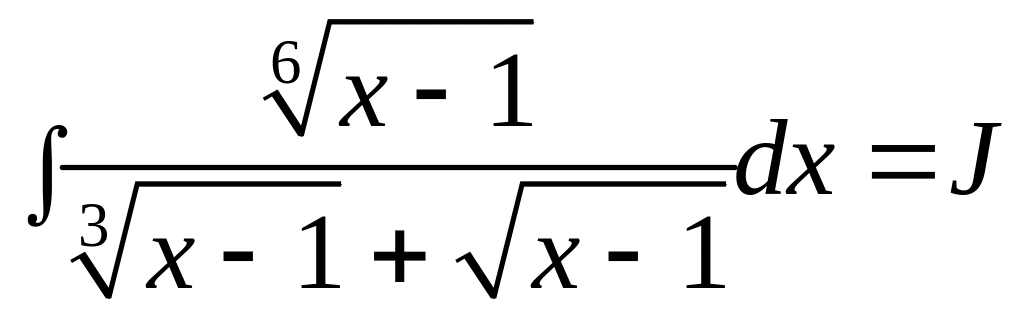 .
.
Под
интегралом стоит иррациональная функция.
Приведем ее к рациональной с помощью
подстановки
![]() ,
где
,
где
![]() - наименьшее общее кратное показателей
корней. Тогда
- наименьшее общее кратное показателей
корней. Тогда
![]() ,
,
![]() .
.
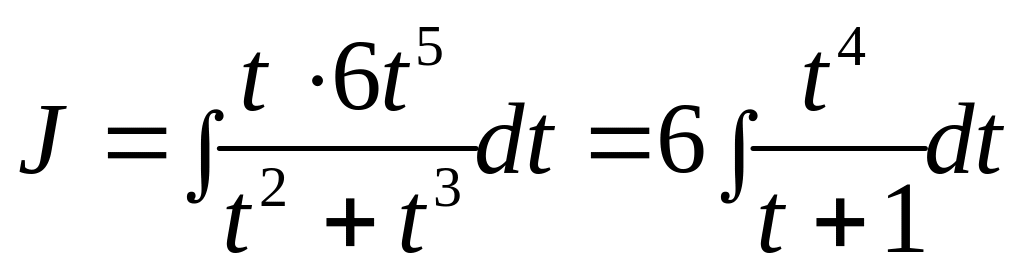 .
Разделим “уголком” числитель
.
Разделим “уголком” числитель
![]() на знаменатель
на знаменатель
![]() .
Получим
.
Получим
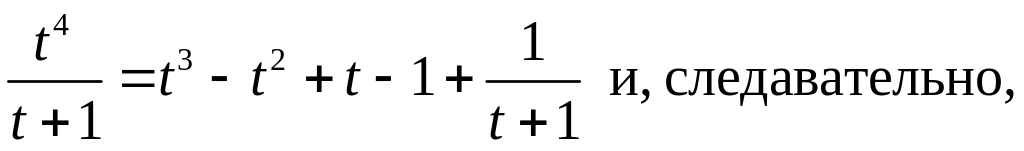
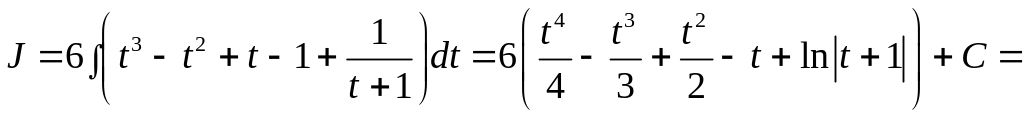
![]() .
.
е)
![]() .
.
Интегралы
вида
![]() ,
где
,
где
![]() – рациональная функция, приводятся к
интегралам от рациональной функции
нового аргумента с помощью универсальной
тригонометрической подстановки
– рациональная функция, приводятся к
интегралам от рациональной функции
нового аргумента с помощью универсальной
тригонометрической подстановки
![]() .
В результате имеем
.
В результате имеем
 .
.
 .
.
Задача
8. Найти
площадь фигуры, ограниченной графиками
функции
![]() .
Сделать схематический чертеж.
.
Сделать схематический чертеж.
Решение.
Площадь фигуры, ограниченной графиком
функции
![]() ,
,
п рямыми
рямыми
![]() и осью
и осью
![]() ,
вычисляется по формуле
,
вычисляется по формуле
![]() .
.
Построим фигуру.