Содержание отчета

1. Тема и цель работы.

2. Скриншот набранных команд и результаты вычислений в среде «MatLab».

3. Сделать вывод о том, какое из трех значений коэффициента нужно выбрать, чтобы синтезированная система отвечала заданным требованиям.

4. Используя диаграммы Боде, ответить на вопрос: какое улучшение динамики исходной системы произошло благодаря регулятору?

Лабораторная работа № 6

Тема: Синтез системы управления путем размещения полюсов.

Цель: ознакомиться с методами современной теории управления, используя язык технического программирования «MatLab» или других (напр. SCILAB, GAP).

Теоретические сведения

Классические процедуры синтеза основаны на использовании передаточной функции, синтез путем размещения полюсов основан на использовании модели в переменных состояния. Модель линейной непрерывной системы в переменных состояния имеет вид:

(6.1)

Мы ограничимся случаем систем с одним входом и одним выходом, поэтому , – это скалярные переменные. Предположим, что вход системы, обозначаемый как , равен нулю (см. рис. 6.1).

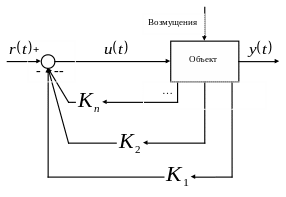
Рис. 6.1. Синтез системы на основе размещения полюсов

В общем случае вход объекта управления является функцией переменных состояния

. (6.2)

Это уравнение называют законом управления. При синтезе путем размещения полюсов закон управления определяется как

, (6.3)

где есть вектор постоянных коэффициентов размерности . Закон управления можно записать в виде:

. (6.4)

Отсюда видно, что сигнал, поступающий на вход объекта, представляет собой линейную комбинацию всех переменных состояния.

Задача синтеза заключается в определении желаемого положения корней характеристического уравнения системы и нахождении коэффициентов , обеспечивающих заданное размещение корней.

Подставляя (6.3) в (6.1), получим

, (6.5)

где есть матрица коэффициентов замкнутой системы. Тогда можно записать характеристическое уравнение замкнутой системы

. (6.6)

Предположим, что по условиям синтеза корни характеристического уравнения должны иметь значения . Обычно исходят из следующего условия:

, (6.7)

где – время установления переходных процессов в системе, – постоянная времени объекта. Из всех полюсов в качестве выбирается тот, у которого модуль действительной части имеет наименьшее значение. Желаемое характеристическое уравнение системы тогда можно записать в виде

. (6.8)

В соответствии с процедурой синтеза путем размещения полюсов необходимо найти такую матрицу , чтобы выражения (6.6) и (6.8) были равны друг другу

. (6.9)

Это уравнение содержит неизвестных . Приравнивая в этом уравнении коэффициенты при одинаковых степенях , мы получим уравнений относительно неизвестных. Эти уравнения являются линейными. Решив их, мы получим элементы матрицы .

В 1972 году Аккерман нашел формулу для вычисления матрицы :

, (6.10)

где – матричный полином, образованный путем использования коэффициентов желаемого характеристического уравнения . Матрица может быть вычислена на компьютере по формуле (6.10). В «MATLAB» матрица вычисляется с помощью команды:

K=acker(A, B, Pp).

Операндами этой команды являются матрицы A и B из уравнения состояния системы, а также Pp – вектор-строка желаемого расположения полюсов системы управления.

Пример синтеза системы управления: Задана модель в пространстве состояний:

, , , .

Необходимо синтезировать замкнутую систему управления с полюсами: . Это значит, нужно найти матрицу-строку . Ниже приводится программа «MatLab», с помощью которой выполняется синтез и вычисляется реакция системы на начальные условия .

A=[0 1; 0 0]; B=[0; 1]; C=[1 0]; D=0;

Pp=[-4+4*i -4-4*i];

K=acker(A, B, Pp), pause

Sp=ss((A-B*K), B, C, D);

initial(Sp, [1; 0])