Содержание отчета
Тема и цель работы.
2. Скриншот набранных команд и результаты вычислений в среде «MatLab».
Сделать выводы об устойчивости систем (3.2), (3.3) и (3.4) в замкнутом состоянии.
Краткие впечатления о программе «SISO Design Tool».
Лабораторная работа № 4
Тема: Диаграмма Найквиста. Запас устойчивости замкнутой системы по модулю и по фазе.
Цель: ознакомиться с диаграммой Найквиста и с понятием условной устойчивости замкнутой системы, научиться определять запасы устойчивости по модулю и по фазе на основе диаграмм Найквиста и Боде, а также с помощью программных средств среды программирования «MatLab» или других (напр. SCILAB, GAP).
Теоретические сведения
Продолжаем изучение замкнутых систем. Напомним, что замкнутой называется система, изображенная на рис. 4.1.
Рис. 4.1
Линия со стрелкой, соединяющая выход объекта с его входом, соответствует так называемой обратной связи. Поскольку сигнал обратной связи в данном случае передается на вход объекта со знаком «минус» (обратите внимание на символы внутри круга), то данная обратная связь называется отрицательной. В линию обратной связи может быть включено еще какое-либо звено (на рисунке не показано). Если такого звена нет, то передаточная функция замкнутой системы определяется выражением
, (4.1)
где – передаточная функция разомкнутой системы.
Диаграмма Найквиста позволяет определить устойчивость замкнутой системы по ее частотным характеристикам в разомкнутом состоянии. На рис. 4.2 показаны диаграммы Найквиста двух разных систем. Левая (а) соответствует системе, которая в замкнутом виде является неустойчивой («петля» охватывает красный крестик, находящийся в точке (–1, 0) – критерий устойчивости Найквиста). Правая (б) – системе, которая в замкнутом виде устойчивая («петля» не охватывает красный крестик).
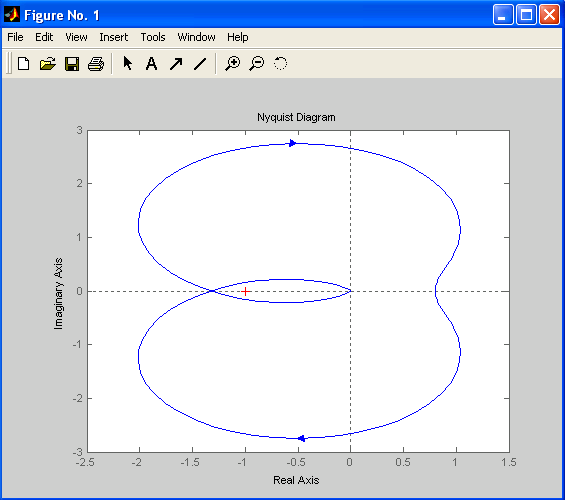
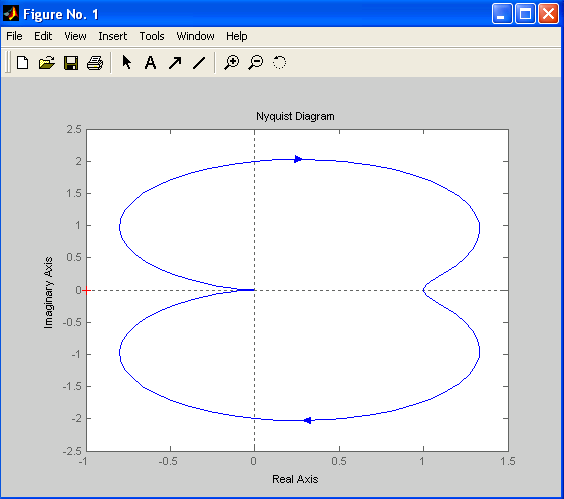
а) б)
Рис. 4.2
Если информация о передаточной функции разомкнутой системы уже введена в программу, то диаграмму Найквиста можно получить с помощью команды: nyquist(G).
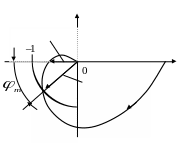
Рис. 4.3
На рис. 4.3 показана
нижняя часть диаграммы Найквиста
системы, устойчивой
в замкнутом состоянии.
Точка пересечения графиком горизонтальной
линии с координатами (
),
как можно видеть, находится правее точки
(–1, 0). Запас
устойчивости по модулю
равен:
,
а запас по
фазе – углу
(см. рис. 4.3).
Запасы устойчивости по модулю и по фазе замкнутой системы можно определить также с помощью диаграммы Боде (рис. 4.4).
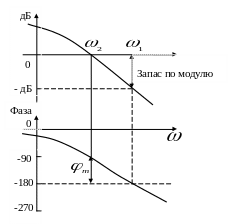
Рис.4.4
Запас по модулю
определяется на частоте, при которой
.
Эта частота на диаграмме Боде (рис. 4.4)
обозначена как
.
Запас по модулю принято выражать в
децибелах,
то есть, как
.
Запас по фазе определяется на частоте
,
на которой
(или 0 дБ). Запас по фазе
есть разность между
и
,
как показано на рисунке.
В системе «MatLab» запасы устойчивости по модулю и по фазе замкнутой системы можно определить с помощью команды:
[Gm, Pm, Wcg, Wcp]=margin(G),
где G – передаточная функция разомкнутой системы. Символы означают: Gm – запас устойчивости по модулю, Pm – запас устойчивости по фазе, Wcg – частота, на которой определяется запас устойчивости по модулю (на рис. 4.3 она обозначена как ), Wcp – частота, на которой определяется запас устойчивости по фазе (на рис. 4.3 она обозначена как ).