§4. Непрерывные функции нескольких переменных

4.1. Определение непрерывности (разрыва) функции нескольких переменных в точке

Пусть функция f(x₁,х₂, ... ,х_n) определена в некотором множестве D точек n-мерного пространства, и М₀ есть точка сгущения этого множества, принадлежащая самому множеству.

Определение 1. Функция f(x₁, х₂, ..., х_n), называется непрерывной в точке М₀ , если существует предел функции f в точке М₀, который равен значению функции в этой точке f , т.е.

. (2.5)

Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.

Это определение в расширенном виде повторяет первое определение непрерывности, данное для функции одной переменной.

Аналогично можно перенести другие определения о непрерывности функции в точке одной переменной на случай функции многих переменных.

Определение 2. Функция f(x₁,х₂, ... ,х_n), называется непрерывной в точке М₀ , если для любого ε > 0 можно указать такое δ_ε > 0, зависящее от ε, что

| f (x₁,х₂, _{. . .},х_n) – f | < ε (2.6)

лишь только

| x₁ – х₁⁰| < δ_ε, | x₂ – х₂⁰| < δ_ε, ... , | x_n – х_n⁰| < δ_ε;

или иначе:

| f (М) – f (М₀) | < ε (2.7)

лишь только расстояние

d(MM₀) < δ_ε.

При этом точка М(x₁,х₂,...,х_n) предполагается принадлежащей множеству D.

Рассматривая разности x₁ – х₁⁰, x₂ – х₂⁰, ... , x_n – х_n⁰ как приращения х₁⁰, х₂⁰, ... , х_n⁰ независимых переменных, а разность

f (x₁,х₂, ... ,х_n) – f (2.8)

– как приращение или как полное приращение f (x₁, х₂, ... ,х_n) функции f в точке М₀ , можно сказать (как в случае функций одной переменной), что функция непрерывна, если бесконечно малым приращением независимых переменных отвечает бесконечно малое же приращение функции, т.е.

. (2.9)

Для функции f(x₁, х₂, ... , х_n) нескольких переменных можно определить понятие непрерывности по одной из переменных при фиксированных значениях остальных переменных. Для определения этого понятия рассмотрим так называемые частные приращения функции f(x₁, х₂,…, х_n) в произвольной точке М  из D. Зафиксируем все аргументы, кроме первого, а первому аргументу придадим произвольное приращение х₁ такое, чтобы точка с координатами х₁ + х₁, х₂, …, х_n находилась в области D задания функции. Соответствующее приращение функции называется частным приращением функции в точке М  , соответствующим приращению х₁ аргумента х₁, и обозначается f( ). Таким образом,

f = (2.10)

Термин «частное приращение» употребляется для того, чтобы отличить это приращение от полного приращения (2.8), соответствующего произвольным приращениям х₁, х₂,…, х_n всех аргументов .

Аналогично определяются частные приращения функции, соответствующие приращениям других аргументов:

. (2.11)

Введем теперь понятие непрерывности функции f( ) по одной из переменных.

Определение 3. Функция f( ) называется непрерывной в точке М₀ по переменной x_i, i = 1, 2, ... , n, если бесконечно малому приращению переменной x_i соответствует бесконечно малое частное приращение функции f , т.е. если

. (2.12)

При фиксированных значениях всех переменных, кроме переменной x_i, функция f( ) представляет собой функцию одной этой переменной. Отметим, что непрерывность функции по переменной x_i означает непрерывность указанной функции одной переменной. Очевидно, из условия (2.5) непрерывности функции f( ) в данной точке M₀ вытекает непрерывность этой функции в точке M₀ по каждой из переменных в отдельности, а также по каждой паре переменных x_i, x_j и т.д. Однако, из непрерывности функции в точке M₀ по каждой из переменных не вытекает, вообще говоря, непрерывность функции в этой точке. Действительно, рассмотрим функцию

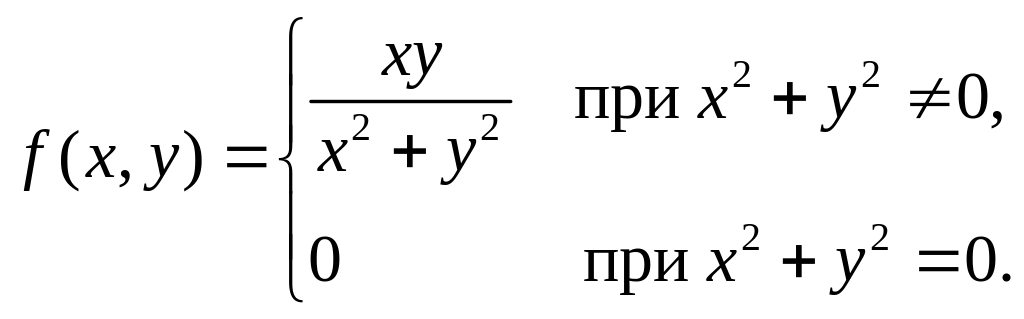
Данная функция, хотя и не является непрерывной в точке M₀(0,0) по обеим переменным сразу (так как мы установили, что в точке (0,0) для этой функции двойного предела не существует (см. гл.2, §3, п.3.2), тем не менее, будет непрерывна в этой точке как по x, так и по y в отдельности; это следует из того, что и .

Сказанное становится понятным, если принять во внимание, что, говоря о непрерывности по х и по у в отдельности, мы учитываем приближение к точке (0,0) лишь вдоль по оси х или по оси у, оставляя в стороне бесчисленное множество других законов приближения.

Если для функции f(M) при стремлении M к M₀ вовсе не существует определенного конечного предела , то говорят, что в точке М₀ функция имеет разрыв, даже в том случае, когда в самой точке М₀ функция не определена.

Точки разрыва функции могут не только быть изолированными, но и заполнять собою линии, поверхности и т.п. Так, функции двух переменных

имеют разрывы: первая – вдоль прямых , а вторая – вдоль окружности .

Определение 4. Функция f( ) называется непрерывной на множестве (в области) D, если она непрерывна в каждой точке этого множества.