
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Критерий сходимости несобственного интеграла от неотрицательной функции.
Теорема 3. Пусть
функция
 неотрицательна и
неотрицательна и

 .
Тогда для сходимости несобственного
интеграла
,
необходимо и остаточно, чтобы существовало
такое
.
Тогда для сходимости несобственного
интеграла
,
необходимо и остаточно, чтобы существовало
такое
 ,
что
,
что
 . Теорема
сравнения, позволяет установить только
абсолютную сходимость несобственного
интеграла. Следующая теорема дает
достаточный признак сходимости, пригодный
и в случае условной сходимости.
. Теорема
сравнения, позволяет установить только
абсолютную сходимость несобственного
интеграла. Следующая теорема дает
достаточный признак сходимости, пригодный
и в случае условной сходимости.
Признак сходимости
Дирихле для несобственных интегралов.Теорема
4 (Признак
сходимости Дирихле). Пусть функции
и
определены на полуоси
,
причем 1) функция
непрерывна на полуоси
и имеет на ней ограниченную первообразную
;2)
функция
– непрерывно дифференцируема и не
возрастает на полуоси
,
а также является бесконечно малой при
 .Тогда
несобственный интеграл
.Тогда
несобственный интеграл (1)сходится.
(1)сходится.
Интегральный признак сходимости числового ряда.
Теорема 1.
Если функция
неотрицательна и не возрастает на
полуоси
 ,
то для того, чтобы числовой ряд
,
то для того, чтобы числовой ряд (1)
(1)
сходился, необходимо и достаточно, чтобы сходился интеграл
|
|
Д о к а з а т е л ь
с т в о. В силу монотонности функции
на полуоси
она интегрируема на любом конечном
отрезке
 ,
,
 ,
и поэтому имеет смысл говорить о
несобственном интеграле (2).
,
и поэтому имеет смысл говорить о
несобственном интеграле (2).
Так как функция
не возрастает на полуоси
,
то каковы бы ни были натуральное
и
 имеет место неравенство
имеет место неравенство проинтегрировав
которое по промежутку
проинтегрировав
которое по промежутку
 получим
получим .
.
Таким образом, для любого натурального имеет место неравенство
 .
.
Просуммировав такие неравенства от 1 до , получим
 ,
,
или, что то же самое,
|
|
где
 ,
– частичные суммы ряда (1).
,
– частичные суммы ряда (1).
Если интеграл (2) сходится, то из неравенств (3), с учетом неотрицательности функции , следует, что последовательность частичных сумм ряда (1) ограничена сверху:

и, следовательно, ряд (1) сходится.
Если же интеграл
(2) расходится, то в силу неотрицательности
функции
,
очевидно, имеем ,
,
а тогда из правой
части неравенства (3) также следует, что
 .
Последнее означает, что ряд (1) расходится
□
.
Последнее означает, что ряд (1) расходится
□
Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
Скалярным
произведением векторов

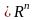 и
и
 называется вещественное число
называется вещественное число
 ,
которое определяется посредством
следующего равенства:)(1)
,
которое определяется посредством
следующего равенства:)(1)
|
|
Длиной вектора
 или также его евклидовой нормой называется
вещественное число
или также его евклидовой нормой называется
вещественное число
 ,
определяемое равенством
,
определяемое равенством
Для любых векторов
|
|
причем равенство
здесь имеет место тогда и только тогда,
когда векторы
и
 линейно зависимы.
линейно зависимы.
Д о к а з а т е л ь
с т в о. Пусть векторы
и
линейно зависимы. Тогда либо
 для некоторого
для некоторого
 ,
либо
,
либо
 для некоторого
для некоторого
 .
Очевидно, достаточно рассмотреть только
один из этих случаев. Пусть, например,
для некоторого
.
Тогда, с учетом того, что в силу 2*
и 6*
.
Очевидно, достаточно рассмотреть только
один из этих случаев. Пусть, например,
для некоторого
.
Тогда, с учетом того, что в силу 2*
и 6*

имеем:

Пусть теперь
векторы
и
линейно независимы. Тогда
 для любого
.
Поэтому
для любого
.
Поэтому

 .Следовательно,
квадратный трехчлен от
.Следовательно,
квадратный трехчлен от
 ,
стоящий здесь справа, не имеет вещественных
корней. Но тогда его дискриминант –
отрицательный, т.е.
,
стоящий здесь справа, не имеет вещественных
корней. Но тогда его дискриминант –
отрицательный, т.е.
 .
Отсюда следует, что в рассматриваемом
случае неравенство (4) – строгое □
.
Отсюда следует, что в рассматриваемом
случае неравенство (4) – строгое □
Евклидова норма и евклидово расстояние: определения и свойства.
Длиной вектора или также его евклидовой нормой называется вещественное число , определяемое равенством
Свойства евклидовой нормы:
1о.
 и
и

(свойство положительной определенности)
2о.

(свойство положительной однородности)
3о.

(неравенство треугольника)
Расстоянием между точками и в пространстве или, точнее, евклидовым расстоянием между ними называется вещественное число
 ,
которое определяется посредством
равенства (5)
,
которое определяется посредством
равенства (5)
|
Свойства евклидова расстояния
1#.
 и
и
 ;
;
2#.
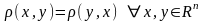 ;
;
3#.
 нерав
треугол
нерав
треугол
Понятие предела последовательности в . Сходящиеся и расходящиеся последовательности в . Понятие ограниченной последовательности в .Теоремы о единственности предела и об ограниченности
сходящейся последовательности в . Теорема Больцано-Вейерштрасса.
Точка
называется пределом последовательности
 точек
пространства
,
если для любого
существует такой номер
точек
пространства
,
если для любого
существует такой номер
 ,
что
,
что

 для всех
для всех
 .
.
Последовательность
точек
 в пространстве
называется сходящейся, если она имеет
предел.
в пространстве
называется сходящейся, если она имеет
предел.
Последовательность
называется ограниченной, если множество
ее значений ограничено, т.е. если
существует такое
 ,
что
,
что

 .
.
Теорема 3. Всякая сходящаяся последовательность точек является ограниченной.
Д о к а з а т е л ь
с т в о. Пусть последовательность
и
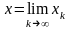 .
Тогда, в частности, для
найдется такое
,
что
.
Тогда, в частности, для
найдется такое
,
что
 .
Поэтому ясно, что все члены последовательности
содержатся в замкнутом шаре с центром
в точке
и радиусом
.
Поэтому ясно, что все члены последовательности
содержатся в замкнутом шаре с центром
в точке
и радиусом
 □
□
Теорема 4 (Больцано-Вейерштрасса). Всякая ограниченная последовательность точек пространства содержит сходящуюся подпоследовательность.( нет доказ)
Понятие
 -
окретногсти точки в
и геометрическая форма определения
предела последовательности в
.
-
окретногсти точки в
и геометрическая форма определения
предела последовательности в
.
Открытым шаром с
центром в точке
 и радиусом
или, также,
-окрестностью
точки
называется множество
и радиусом
или, также,
-окрестностью
точки
называется множество
 .
.
точка
называется пределом последовательности
,
если для любого
существует такое
,
что
 для всех
.
для всех
.

 .(2)
.(2) ,
(3)
,
(3)

 ,
,
 и
и
 имеет место
неравенство Коши-Буняковского:
имеет место
неравенство Коши-Буняковского:
 ,
,