Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.

Пусть функция определена на промежутке и интегрируема по Риману на любом конечном отрезке , .Определение 1. Если существует конечный предел ,(1) то его называют несобственным интегралом 1-го рода функции на промежутке и обозначают символом (2).Таким образом, ,(3) при этом если существует конечный предел (1), то говорят, что несобственный интеграл (2) сходится; в противном случае, говорят, что он расходится. Замечание 1. Если , то интегралы и сходятся или нет одновременно. Действительно, так как то пределы и существуют или нет одновременно. Замечание 2. Если в дополнение к сделанным выше предположениям функция имеет на промежутке первообразную , то и в силу (3) имеем: 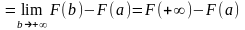,где .

Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.

Пусть функция определена и неограничена на полуинтервале , но интегрируема на любом отрезке , , 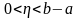а значит и ограничена на любом таком отрезке. В указанном случае точка называется особой точкой функции . Предел ,(1) вне зависимости от того существует он или нет, называют несобственным интегралом второго рода с особенностью на верхнем пределе интегрирования и обозначают его (увы, быть может) так же как обыкновенный определенный интеграл символом .(2) Таким образом, = . (3)Если предел (1) существует и конечен, то говорят, что несобственный интеграл (2) сходится. В противном случае говорят, что несобственный интеграл (2) расходится. Аналогично вводится понятие несобственного интеграла второго рода с особенностью на нижнем пределе интегрирования. А именно пусть функция определена и неограничена на полуинтервале , но интегрируема на любом отрезке , . В этом случае уже точку называют особой. Формально несобственный интеграл второго рода (обозначаемый ниже тем же, что и выше, символом (2)) определяется равенством , при этом если здесь предел существует и конечен, то говорят, что соответствующий интеграл сходится; в противном же случае говорят, что он расходится. Формально к числу несобственных интегралов 2-го рода относятся и обычные (собственные) римановские интегралы, которые очевидно являются сходящимися.

Основные свойства несобственных интегралов: аддитивное свойство, линейное свойство, интегрирование неравенства, формула Ньютона-Лейбница .1^о. Свойство аддитивности. Каково бы ни было несобственные интегралы (с особенностью на верхнем пределе интегрирования) и (1) сходятся или нет одновременно, при этом в случае сходимости имеет место равенство (здесь первый из интегралов справа –собственный) (2) 2^о. Линейное свойство. Если несобственные интегралы и (3) сходятся, то для любых вещественных чисел и сходится и интеграл , (4) при этом (5). 3^о. Интегрирование неравенства. Если несобственные интегралы (3) сходятся и , то .(6)4^о.Формула Ньютона-Лейбница. Если функция на любом отрезке 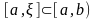интегрируема по Риману и имеет на нем первообразную , то справедлива формула Ньютона-Лейбница: (7)