Число e как сумма ряда.

Всюду далее по определению считаем, что при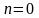 . Для любого натурального и любого положим ≜ .Число называется числом сочетаний из по 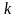или, также, биномиальным коэффициентом. Так как , то из определения биномиальных коэффициентов следует, что . Непосредственной проверкой можно убедиться в справедливости следующих свойств биномиальных коэффициентов: .Индукцией по можно доказать, что для любых вещественных чисел и и любого натурального имеет место равенство 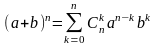. Теорема 6. Ряд (4) сходится и его сумма равна числу : (5)Д о к а з а т е л ь с т в о. Для членов ряда (4), очевидно, что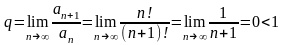 . Поэтому по признаку Д’аламбера он сходится.Пусть , .Поскольку ≜ , то с учетом определения суммы ряда для доказательства равенства (5) достаточно доказать, что = (6) По формуле бинома Ньютона (при ) имеем .

Следовательно . Переходя в этом неравенстве к пределу при будем иметь . (7) Заметим теперь, что если , то .Фиксируя здесь и переходя к пределу при , получим Теперь переходя в этом неравенстве к пределу при , будем иметь . (8) Из (7) и (8) следует (6) □

Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда

Определение 1. Ряд вида (1) где , называется знакочередующимся. Теорема (признак Лейбница). Если абсолютные величины членов знакочередующегося ряда образуют невозрастающую, бесконечно малую последовательность, т.е. 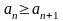, и , то он сходится.Д о к а з а т е л ь с т в о. Пусть – последовательность частичных сумм ряда (1). Рассмотрим две ее подпоследовательности и , соответственно с четными и нечетными номерами. Так как , то последовательность не убывает: , а последовательность не возрастает: . В свою очередь, так как последовательность не возрастает и то . Следовательно, последовательность не только не убывает, но и ограничена сверху. Поэтому она сходится. Пусть . (2) Тогда 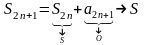при , т.е. (3) Из (2) и (3) следует, что , т.е. ряд (1) сходится ■

Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.

Теорема 1. Если ряд (1) сходится, то сходится и ряд .(2) Определение 1. Числовой ряд (2) называется абсолютно сходящимся, если сходится ряд (1). Определение 2. Числовой ряд (2) называется условно сходящимся, если он сходится, но ряд (1), составленный из модулей его членов, расходится.

Понятие перестановки числового рядов. Теорема Римана и ее иллюстрация на примере ряда . Определение 3. Пусть дан некоторый ряд и –биективное отображение. Тогда ряд называется перестановкой ряда .Теорема 2 (Римана). Пусть ряд сходится условно. Тогда каково бы ни было вещественное число существует такая перестановка этого ряда , которая имеет своей суммой это число, т.е. .

Теорема о перестановке абсолютно сходящегося ряда.

Если ряд сходится абсолютно, то любой ряд, полученный в результате перестановки его членов, также сходится абсолютно и имеет ту же сумму.

Понятие функциональной последовательности (ф.п.) и ее области определения; 2)понятие сходимости ф.п. в точке 3) понятие сходимости ф.п. на множестве; 4)понятие области сходимости ф.п.;5) понятие предельной функции ф.п.

1)Пусть 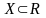. Отображение натурального ряда 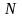во множество всех функций, определенных на множестве 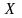называется функциональной последовательностью, при этом множество называется областью определения функциональной последовательности , а функции , , образующие эту последовательность называются ее членами.

2)Пусть – область определения функциональной последовательности (или функционального ряда (1)) и 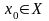. Определение 1. Если числовая последовательность 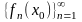(соответственно, числовой ряд ) сходится, то говорят, что функциональная последовательность (соотв., функциональный ряд (1)) сходится в точке .

3) Определение 2. Если функциональная последовательность (функциональный ряд) сходится в каждой точке некоторого множества 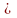, то говорят что она (соотв., он) сходится на этом множестве. 4)Определение 3. Множество всех точек, в каждой из которых сходится данная функциональная последовательность (соотв., – данный функциональный ряд), называется областью сходимости этой последовательности (этого ряда).

5)Если функциональная последовательность сходится на множестве , то на нем можно определить функцию , положив в каждой точке , 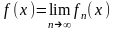. Так определенную функцию называют предельной функцией последовательности на множестве .

Понятие функционального ряда (ф.р.) и области его определения; 2)понятие сходимости ф.р. в точке ; 3)понятие сходимости ф.р. на множестве и 4)понятие области сходимости ф.р.; понятие суммы ф.р.

1.Если на множестве задана функциональная последовательность 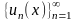, то формальную сумму всех ее членов (1)называют функциональным рядом, при этом члены последовательности называются членами функционального ряда (1), а область определения этой последовательности– областью определения ряда (1). Как и в случае числового ряда, сумма первых членов ряда (1) называется -ой частичной суммой этого ряда. 2)Пусть – область определения функционального ряда и . Определение 1. Если числовой ряд сходится, то говорят, что функциональный ряд сходится в точке .3)Определение 2. Если функциональный ряд (1) сходится в каждой точке некоторого множества , то говорят что он сходится на этом множестве.

4)Множество всех точек, в каждой из которых сходится данный функциональный ряд, называется областью сходимости этой последовательности (этого ряда).

5) Если функциональный ряд (1) сходится на множестве , то на этом множестве можно определить функцию , положив в каждой точке , ,(2) где – -ая частичная сумма функционального ряда (1). Функция , определенная равенством (2), называется суммой функционального ряда (1) на множестве .

Понятие степенного ряда. Теорема Коши-Адамара. Радиус сходимости, интервал сходимости и область сходимости степенного ряда.

Степенным рядом называется функциональный ряд вида 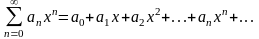(1) в котором – заданные вещественные числа, называемые коэффициентами этого ряда. Ясно, что функциональный ряд более общего вида (2) после замены приводится к виду (1). Ряды такого вида также называются степенными. Теорема 1 (теорема Коши-Адамара). 1^о. Если последовательность 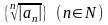неограничена, то степенной ряд (1) сходится только в точке . 2^о. Если последовательность ограничена и , то ряд (1) абсолютно сходится при всех , и расходится при всех . 3^о. Если последовательность ограничена и , то ряд (1) абсолютно сходится для всех вещественных . Число 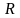найдем по формуле (если

, то по определению здесь считается, что ). Это число называется радиусом сходимости степенного ряда (1), а интервал 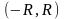– интервалом сходимости этого ряда.