Глава 4. Решение задачи коши методом конечных разностей

1. Методы эйлера и тейлора

Подавляющее большинство алгоритмов решения задачи Коши разработаны для уравнения первого порядка . Простейшим является метод Эйлера. Аппроксимируя производную правой разностью, получим

Функция может вычисляться либо в момент , либо в момент . В первом случае имеем явную одношаговую разностную схему

(4.1)

Во втором случае имеем неявную одношаговую разностную схему

(4.2)

Она в общем случае есть нелинейное уравнение относительно , решение которого может быть получено итерационными методами.

Явная схема проще в реализации и интерпретации (рис. 4.1).

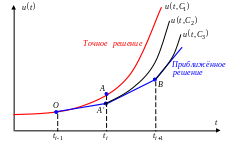
Рис. 4.1 Геометрическая интерпретация метода Эйлера

Она описывает переход с одной интегральной кривой уравнения на другую по локальной касательной. Поэтому приближённое решение неизбежно отклоняется от точного решения. Погрешность на одном шаге равна отрезку .

Уменьшить погрешность можно, экстраполируя решение на каждом шаге разложением в ряд Тейлора вплоть до N-го порядка включительно,

Входящие в (4.3) производные можно вычислить, дифференцируя по функцию (если она дифференцируема требуемое число раз),

…

Порядок точности алгоритма Тейлора равен числу членов разложения N. В принципе он может быть сделан достаточно высоким. Но за это приходится платить вычислением производных функции , что может оказаться весьма громоздким. Хотелось бы иметь алгоритм, полагающийся на вычисления значений только самой функции в узлах.

4.2 Явные методы рунге - кутты

В. Кутта на основе идей К. Рунге сформулировал в 1901 г. алгоритм уменьшения погрешности за счёт оптимизации наклона линейной экстраполяции решения в узел . По этому алгоритму строится семейство методов Рунге – Кутты. Именно, приближённое решение уравнения в узле записывается в виде

(4.4)

Сумма в скобках в (4.4) есть оптимизированное значение производной функции f, обеспечивающее линейный переход из т.О на интегральную кривую, более близкую к , чем . В зависимости от числа слагаемых q формулы называются одно-, двух-, трёх-, четырёхчленными и т.д. Числа , , , могут быть выбраны так, чтобы порядок точности q-членной формулы равнялся q, то есть погрешность аппроксимации была пропорциональной .

Одночленная формула Рунге – Кутты есть просто явная формула Эйлера. Двухчленные формулы образуют однопараметрическое семейство, в котором

При имеем формулу Хойна

(4.4)

Таким образом, в методе Хойна производная в точке заменяется среднеарифметическим значением производных в точках и (рис. 4.2).

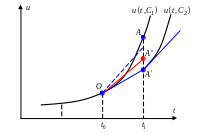
Рис. 4.2 Геометрическая интерпретация формулы Хойна

Широко используемый классический метод Рунге - Кутты 4-го порядка точности задаётся соотношениями

(4.5)

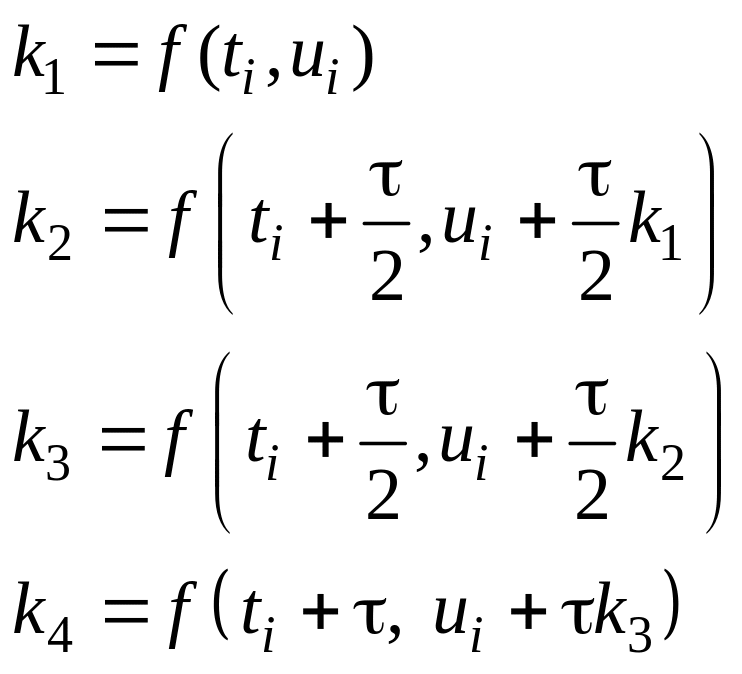
На системы уравнений 1-го порядка методы Рунге – Кутты обобщаются непосредственно. Например, алгоритм решения системы уравнений

(4.6)

по методу Хойна имеет вид

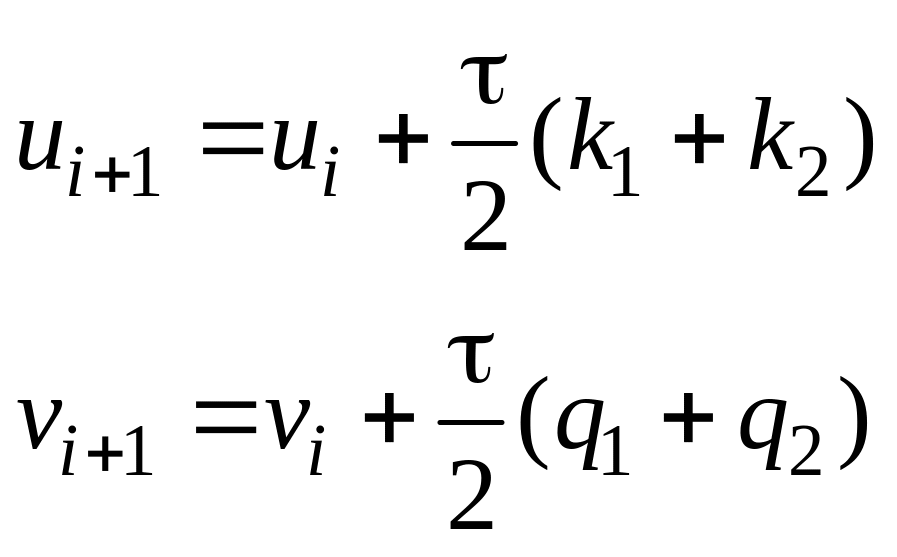(4.7)

Применительно к системе (3.24) из (4.7) следует

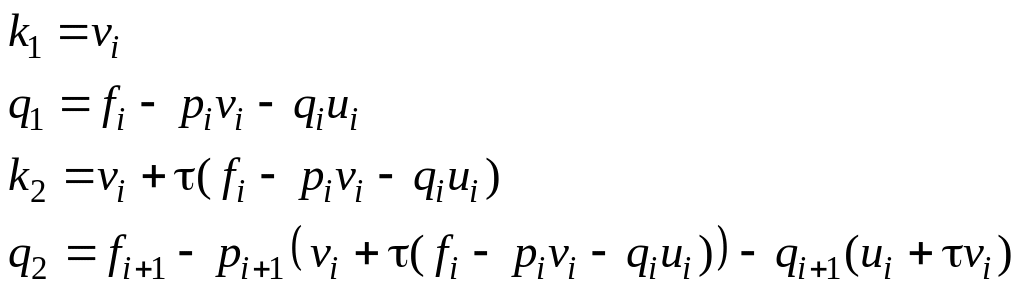(4.8)

Задача. Получить из (4.3) двухчленные формулы Рунге – Кутты 2-го порядка при для системы (3.24), эквивалентной уравнению (3.22).