Конечноразностная аппроксимация обыкновенных дифференциальных уравнений
Линейные обыкновенные дифференциальные уравнения (ОДУ), с которыми приходится иметь дело в реальных задачах, можно записать в достаточно общем виде
(3.21)
или 
(3.22)
Уравнение (3.21) характерно для стационарных задач, уравнение (3.22) – для динамических. Вместо уравнения (3.22) можно решать эквивалентную систему ОДУ первого порядка
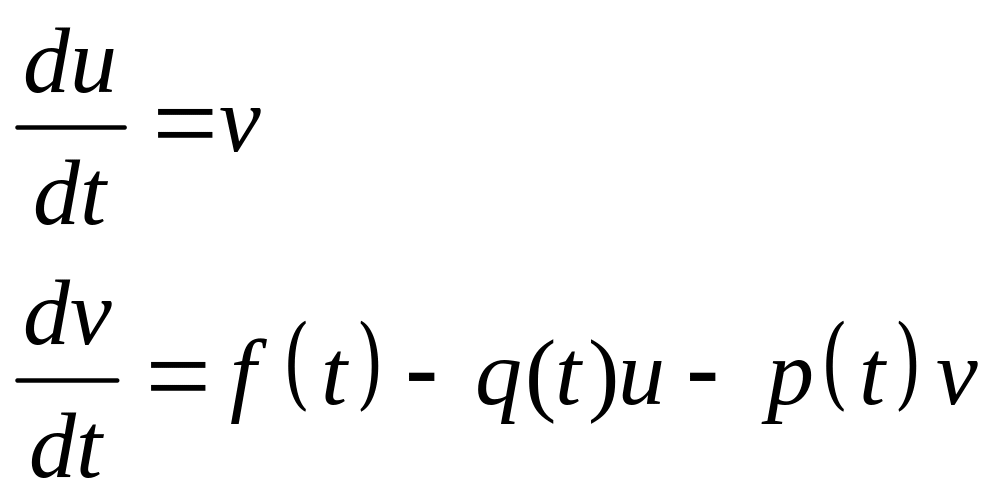(3.23)
Если
ввести векторы
,
,
где знак
обозначает
операцию транспонирования, то система
(3.23) запишется в виде одного векторного
уравнения первого порядка
(
)
Некоторые задачи приводят к системе двух ОДУ 2-го порядка. Такая система описывает, например, движение двух связанных осцилляторов. Механическая реализация системы показана на рис. 3.5.
Рис.3.5. Два осциллятора, связанных упругой связью с жёсткостью k
На
массу
действуют упругие силы
,
обусловленная деформацией собственной
связи с жёсткостью
,
и
,
вызванная деформацией
взаимной связи с жёсткостью
.
Аналогично, на массу
действуют упругие силы
,
обусловленная деформацией собственной
связи с жёсткостью
и
,
вызванная деформацией
той же взаимной связи с жёсткостью
.
При малых смещениях из положения
равновесия деформации также малы, и
силы можно записать по закону Гука в
виде
,
,
где
- мгновенные значения координат масс
и
соответственно,
- их равновесные координаты. Уравнения
движения масс
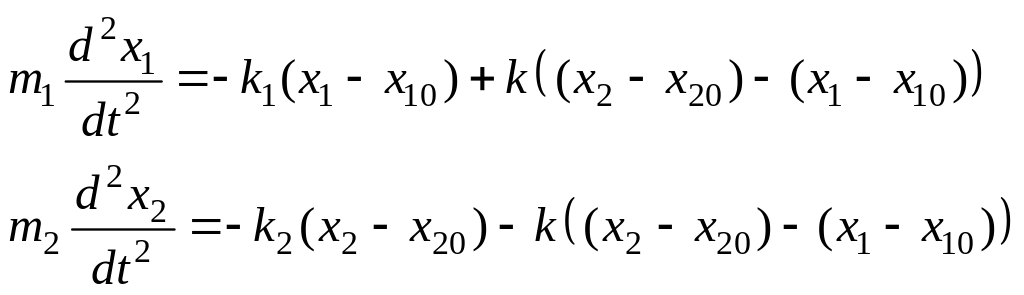
В
переменных
и
они принимают вид
(3.25)
где
,
,
,
.
Система (3.25) описывает осцилляторы в
бездиссипативной среде. При наличии
диссипации вследствие вязкого трения
и при произвольной связи она может быть
записана в виде
(3.26)
Её также можно заменить эквивалентной системой четырёх ОДУ 1-го порядка
(
)
которую,
в свою очередь, записать в векторном
виде
.
Эту процедуру можно применить к системе,
содержащей любое число уравнений
порядка, выше первого.
ОДУ
должно быть дополнено краевыми условиями,
выделяющими частное решение. Краевые
условия различны для временных и
стационарных задач. Динамическое
уравнение (3.22), описывающее эволюцию
изучаемого объекта или процесса,
дополняется начальными условиями
– значениями искомой функции и её
производной в начальный момент времени
,
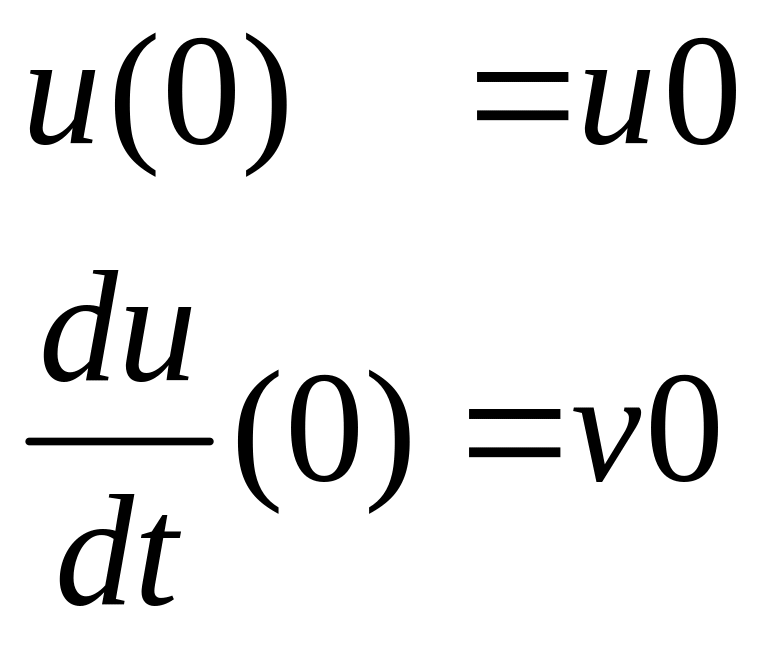(3.28)
Для
системы (3.25) задаётся начальное значения
вектора
.
Начальные условия задают направление
эволюции, тогда как уравнение определяет
её темп.
Стационарные
уравнения типа (3.21) описывают распределение
искомой величины в пространстве. На
границах
области определения
задаются граничные условия.
В зависимости от физического содержания
задачи могут задаваться значения функции
(задача Дирихле)
(3.29)
или её производных (задача Неймана)
(3.30)
либо смешанные условия
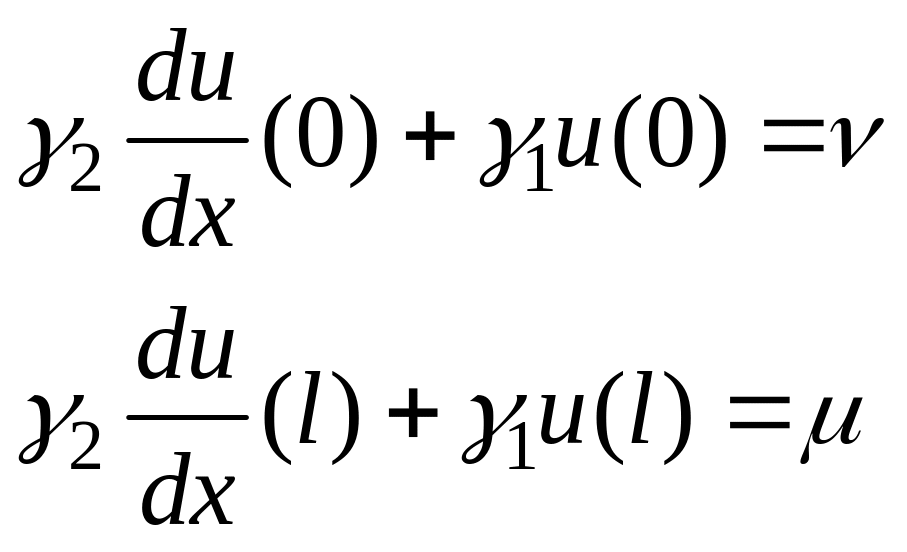(3.31)
Различие в краевых условиях обусловливает различие в методах численного решения задач
Стационарные ОДУ преобразуются в СЛАУ или СНУ посредством аппроксимации всех слагаемых в узлах сетки.
Запишем
уравнение (3.21) во внутренних узлах
граничной сетки
,
,
Первое слагаемое аппроксимируем со вторым порядком точности центральной разностью на шаге h (рис.3.6),
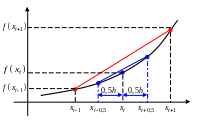
Рис.3.6.
После
приведения подобных членов получаем
уравнение
(3.32)
Граничные условия дают ещё два уравнения. В случае задачи Дирихле они тривиальны,
(3.33)
В случае задачи Неймана производную на левой границе аппроксимируем правой разностью, а производную на правой границе – левой разностью,
(3.34)
Так как аппроксимация (3.34) имеет первый порядок точности, то и порядок аппроксимации задачи в целом понижается до первого. Позже рассмотрим метод повышения порядка аппроксимации граничных условий второго рода.
Таким
образом, в
граничных задачах
ОДУ аппроксимируется
СЛАУ или СНУ, размерность которых равна
числу узлов
,
а
решение находится сразу во всей области
определения.
Решение
эволюционной задачи Коши (3.24) может
быть найдено пошагово,
то есть его значение
в момент
выражается через значения в предшествующие
моменты
,
но не через
Начальные условия
позволяют определить значения решения в двух первых узлах. Решение в следующих узлах строится по аналогии с методом Эйлера численного интегрирования ОДУ первого порядка.
Задача Коши проще граничных задач, поэтому рассмотрим сначала её.