4.4 Подвохи при применении методов рунге-кутты
Основное требование, предъявляемое к приближённому численному решению ОДУ, состоит в минимальном отклонении его от точного решения. Отклонения могут быть обусловлены тремя причинами:
- погрешностью метода
(качеством алгоритма)
;
- неустранимыми ошибками
в начальных данных
;
- погрешностью округления
.
Разность между точным решением задачи Коши
и приближённым,
фактически найденным решением
,
называется полной погрешностью
в узле
,
Все три источника погрешностей дают аддитивные вклады в полную погрешность,
Эволюция
погрешностей зависит от поведения
интегральных кривых ОДУ. Если
,
то есть интегральные кривые расходятся,
то влияние локальных погрешностей,
образовавшихся на предыдущих шагах,
возрастает. Если же
,
то есть интегральные кривые сближаются,
то влияние локальных погрешностей
ослабевает, при дополнительном условии,
что шаг сетки выбран достаточно малым.
Наглядно продемонстрировать последнее утверждение можно с помощью простейшей задачи
,
решением которой
является экспонента
.
Если эту задачу решать методом Эйлера,
то приближённое значение функции
в
-м
узле
может быть выражено через начальное
условие,
Если начальное значение
известно с погрешностью
,
то и
будет вычислено с некоторой погрешностью
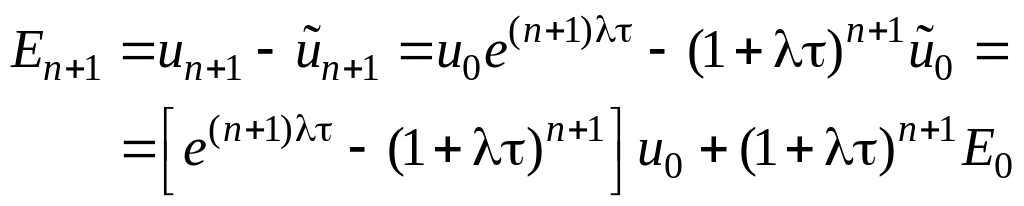
Первое слагаемое даёт погрешность метода
,
обусловленную линейной
аппроксимацией
экспоненты
.
Второе слагаемое
описывает эволюцию ошибки в начальных
данных. При
она рано или поздно, независимо от
,
станет доминировать в суммарной
погрешности
.
Такие задачи называются плохо
обусловленными, а алгоритм –
неустойчивым по отношению к входным
данным. При
погрешность, обусловленная ошибкой в
начальных данных, будет ограниченной,
если
,
или
,
что возможно при
Это ограничение на
шаг называется условием устойчивости.
При больших по абсолютной величине
значениях
шаг по времени приходится брать весьма
малым. Если он окажется меньшим
,
то, как указывалось выше (п.4.2), ошибка
округления
всё равно не позволит получить достаточно
точное решение.
Для системы из N ОДУ
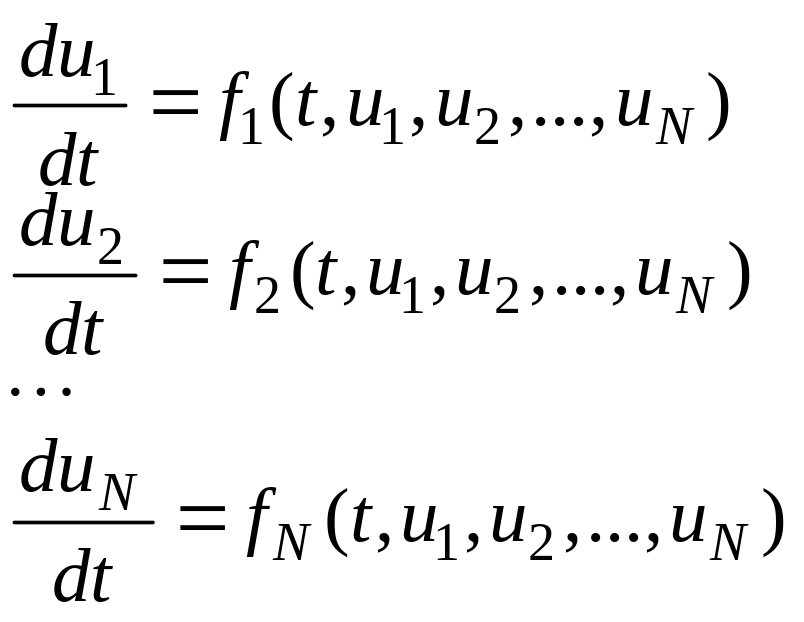
контроль обусловленности производится по собственным значениям якобиана
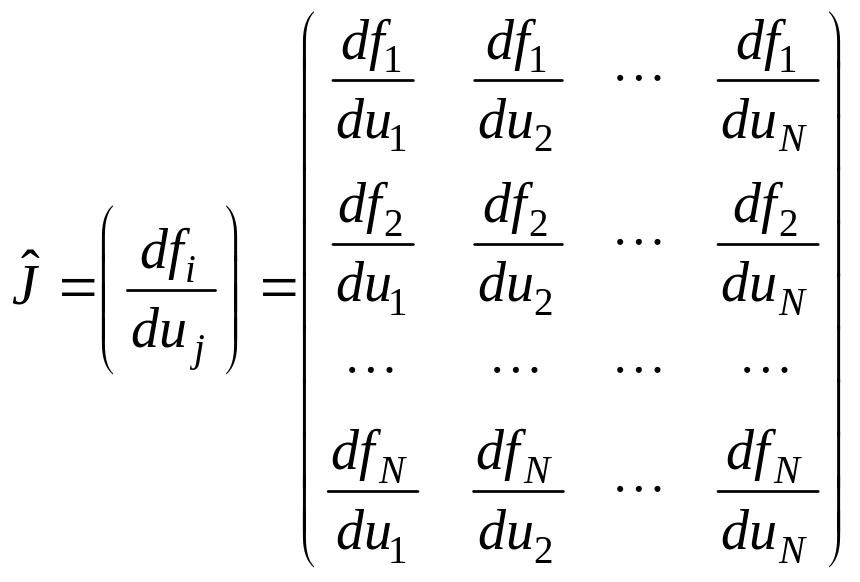
Система будет плохо
обусловленной, если хотя бы у одного из
собственных значений якобиана вещественная
часть положительна. Например, для системы
(3.23)
,
,
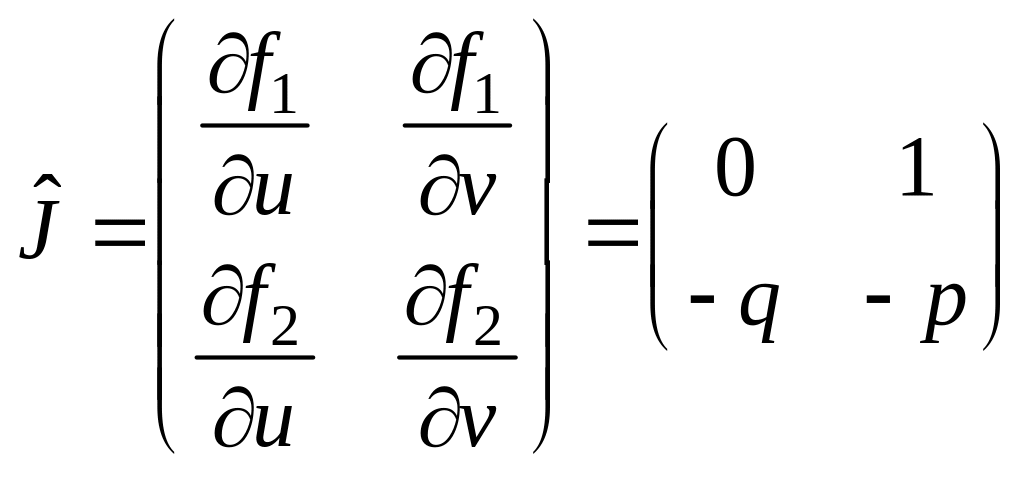
Уравнение для собственных значений имеет вид
или
,
откуда
.
Таким образом, при
система заведомо плохо обусловлена.
Прежде чем приступать к численному решению задачи Коши, следует качественно проанализировать уравнение и выяснить характер его обусловленности. Плохо обусловленные задачи целесообразно переформулировать так, чтобы новые уравнения обладали хорошей обусловленносью. В процессе численного решения целесообразно контролировать локальную обусловленность задачи и, при необходимости, корректировать шаг . Такие алгоритмы с адаптированным шагом получили широкое распространение. В программе MathCAD, например, имеется встроенная функция Rkadapt, реализующая алгоритм Рунге-Кутты с переменным контролируемым шагом.