Тема 8. Дифференциальное исчисление функций нескольких переменных.
Основные теоретические сведения.
1.
Пусть даны два непустых множества D
и U.
Если каждой паре действительных чисел
(x;
y),
принадлежащей множеству D,
по определенному правилу ставится в
соответствии один и только один элемент
u
из U,
то говорят, что на множестве D
задана
функция
f
(или
отображение)
со множеством значений U.
При этом пишут
,
или
,
или
.
Множество D
называется областью определения функции,
а множество U,
состоящее из всех чисел вида
,
где
,
множеством
значений
функции. Значение функции
в
точке
называется частным
значением функции
и обозначается
или
.
2. Частные производные первого порядка.
Частной
производной
от функции
по независимой переменной
называется конечный предел
вычисленный при постоянном .
Частной производной по называется конечный предел
,
вычисленный при постоянном .
Для частных производных справедливы обычные правила и формулы дифференцирования.
3. Полный дифференциал.
Полным
приращением
функции
в точке
называется разность
где
и
произвольные
приращения аргументов.
Функция
называется дифференцируемой в точке
,
если в этой точке полное приращение
можно представить в виде
,
где
.
Полным
дифференциалом
функции
называется главная часть полного
приращения
,
линейная относительно приращений
аргументов
и
,
т.е.
.
Дифференциалы
независимых переменных совпадают с их
приращениями, т.е.
и
.
Полный дифференциал функции вычисляется по формуле
.
Аналогично,
полный дифференциал функции трех
аргументов
вычисляется по формуле
.
При достаточно малом для дифференцируемой функции справедливы приближенные равенства
.
4. Частные производные и дифференциалы высших порядков.
Частными производными второго порядка от функции называются частные производные от ее частных производных первого порядка .
Обозначение частных производных второго порядка:
.
Аналогично определяются и обозначаются частные производные третьих и высших порядков, например:
и
т.д.
Так называемые «смешанные» производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны, например:
.
Дифференциалом
второго порядка от функции
называется дифференциал от ее полного
дифференциала, т.е.
.
Аналогично
определяются дифференциалы третьего
и высших порядков:
;
вообще
Если
x
и y
–
независимые переменные и функция
имеет непрерывные частные производные,
то дифференциалы высших порядков
вычисляются по формулам:
5. Дифференцирование неявных функций.
Производная
неявной функции
,
заданной с помощью уравнения
,
где
дифференцируемая
функция переменных
и
,
может быть вычислена по формуле
при
условии
Производные высших порядков неявной функции можно найти последовательным дифференцированием указанной формулы, рассматривая при этом как функцию от .
Аналогично,
частные производные неявной функции
двух переменных
,
заданной с помощью уравнения
,
где
дифференцируемая
функция переменных
и
,
могут быть вычислены по формулам
при
условии
6. Экстремум функции.
Функция
имеет максимум
(минимум)
в точке
,
если значение функции в этой точке
больше (меньше), чем ее значение в любой
другой точке
некоторой окрестности точки
,
т.е.
[соответственно
]
для всех точек
,
удовлетворяющих условию
,
где
достаточно
малое положительное число.
Максимум или минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума.
Если дифференцируемая функция достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, т.е.
(необходимые условия экстремума).
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
Пусть стационарная точка функции . Обозначим
и
составим дискриминант
Тогда:
а)
если
то функция имеет в точке
экстремум, а именно максимум при
и минимум при
б)
если
то в точке
экстремума нет (достаточные условия
наличия или отсутствия экстремума);
в)
если
то требуется дальнейшее исследование
(сомнительный случай).
Пример
1. Дана
функция
Найти
и
.
Решение.
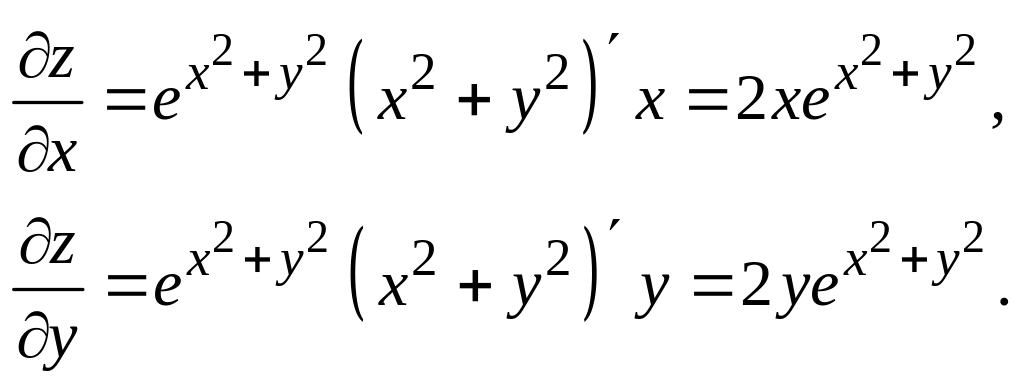
Пример
2.
Дана функция
Найти dz.
Решение.
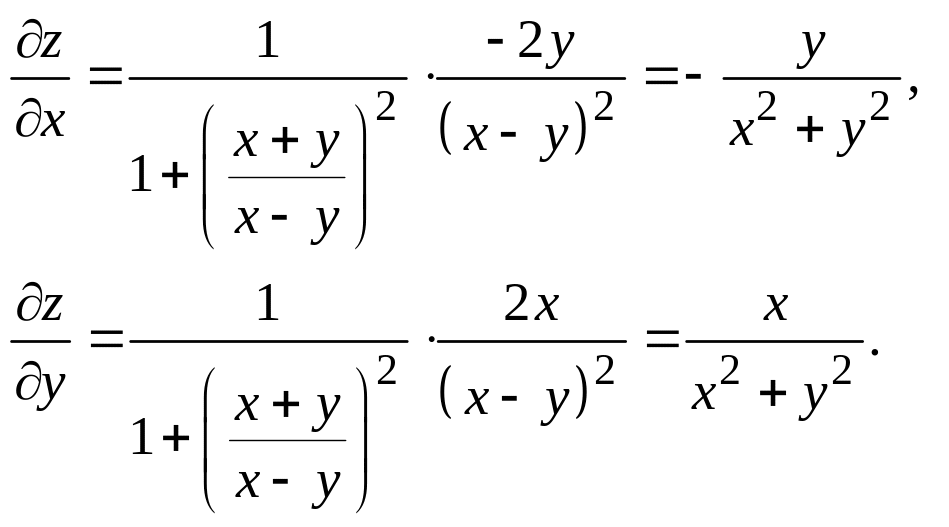
Следовательно,
Пример
3.
Вычислить приближенно
исходя из значения функции
при
Решение.
Искомое число есть наращенное значение
функции z
при
Найдем значение z
при
имеем
Находим приращение функции:
Следовательно,
Пример
4.
Вычислить приближенно
исходя из значения функции
при
.
Решение.
Значение функции z
при x=1,
y=1
есть
Найдем
приращение функции
при
=
Следовательно,
Пример
5.
Найти
Решение.
Здесь
Найдем
Следовательно,
Пример
6.
Найти
и
Решение.
Здесь
=
Находим
Тогда
Пример
7.
Найти экстремум функции
Решение.
Находим частные производные первого
порядка:
Воспользовавшись необходимыми условиями
экстремума, находим стационарные точки:
откуда
Находим значения частных производных второго порядка в точке M:
и
составляем дискриминант
Следовательно, в точке
заданная функция имеет минимум. Значение
функции в этой точке
Пример 6. Найти экстремум функции
Решение. Находим частные производные первого порядка:
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
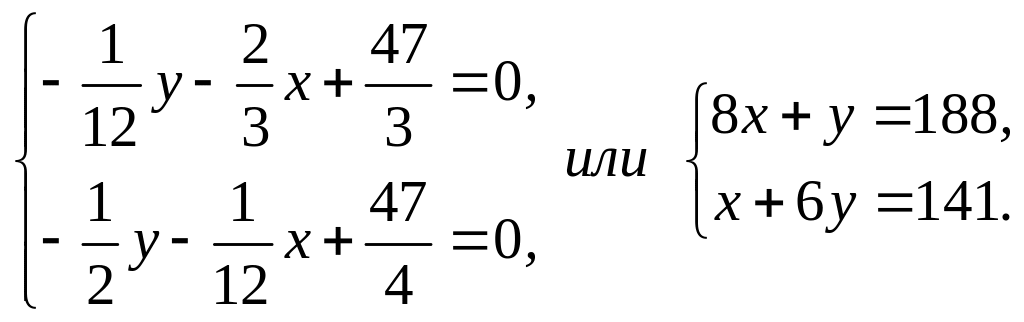
Отсюда
x=21,
y=20;
стационарная точка
Найдем
значения вторых производных в точке M:
Тогда
.
Так
как A<0,
то в точке
функция имеет максимум:
