
- •Тема 1. Элементы линейной алгебры.
- •Тема 2. Элементы векторной алгебры.
- •Тема 3. Аналитическая геометрия.
- •Аналитическая геометрия на плоскости
- •Гипербола
- •Парабола
- •Преобразование координат на плоскости. Построение кривых, заданных общим уравнением
- •Аналитическая геометрия в пространстве.
- •Тема 4. Комплексные числа.
- •Тема 5. Введение в анализ
- •Тема 6. Дифференциальное исчисления функций одной переменной.
- •4. Точки экстремума.
- •5. Точки перегиба.
- •6. Асимптоты.
- •7. Общая схема исследования функции.
- •Тема 7. Интегральное исчисления функций одной переменной.
- •2. Свойства неопределенного интеграла.
- •3. Таблица основных неопределенных интегралов.
- •4. Методы интегрирования.
- •Тема 8. Дифференциальное исчисление функций нескольких переменных.
- •4. Частные производные и дифференциалы высших порядков.
- •5. Дифференцирование неявных функций.
- •Тема 9.Дифференциальные уравнения.
- •Тема 10. Ряды.
- •Тема 11. Элементы теории вероятностей.
- •Задания к выполнению контрольных работ.
- •Задачи для контрольных заданий.
- •Тема 1. Элементы линейной алгебры.
- •Тема 2. Элементы векторной алгебры.
- •Тема 3. Аналитическая геометрия на плоскости.
- •Тема 3. Аналитическая геометрия в пространстве.
- •Тема 4. Комплексные числа.
- •Тема 5. Введение в анализ
- •Тема 6. Дифференциальное исчисления функций одной переменной.
- •Тема 7. Интегральное исчисления функций одной переменной.
- •Тема 8. Дифференциальное исчисление функций нескольких переменных.
- •Тема 9.Дифференциальные уравнения.
- •Тема 10. Ряды.
- •Тема 11. Элементы теории вероятностей.
- •Список литературы
Тема 5. Введение в анализ
№8. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() ;
г)
;
г)![]()
2.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)
![]()
3.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
4.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
5.
а)![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
6.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
7.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
8.
а)
![]() ;
б)
;
б)![]() ;
;
в)
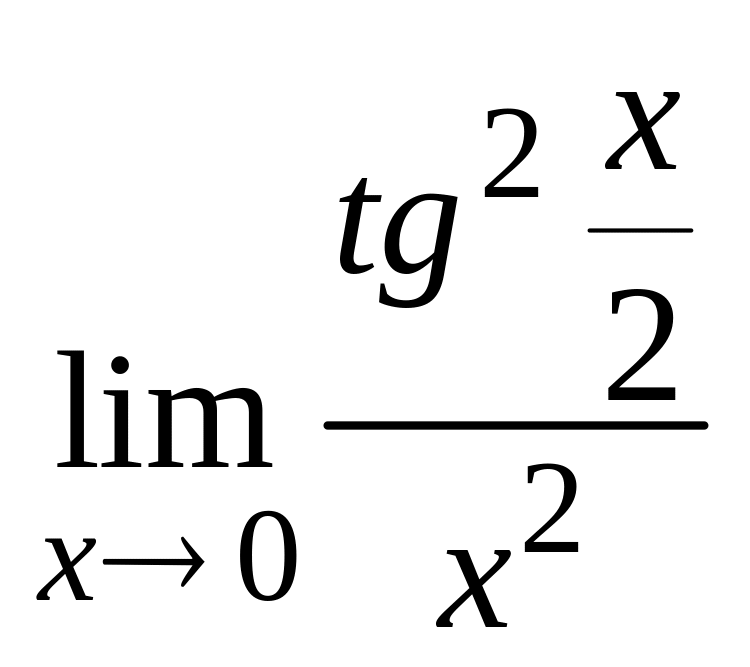 ;
г)
;
г)
![]() .
.
9.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
10.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
11.
а)
![]() ;
б)
;
б)
![]() ;
;
в)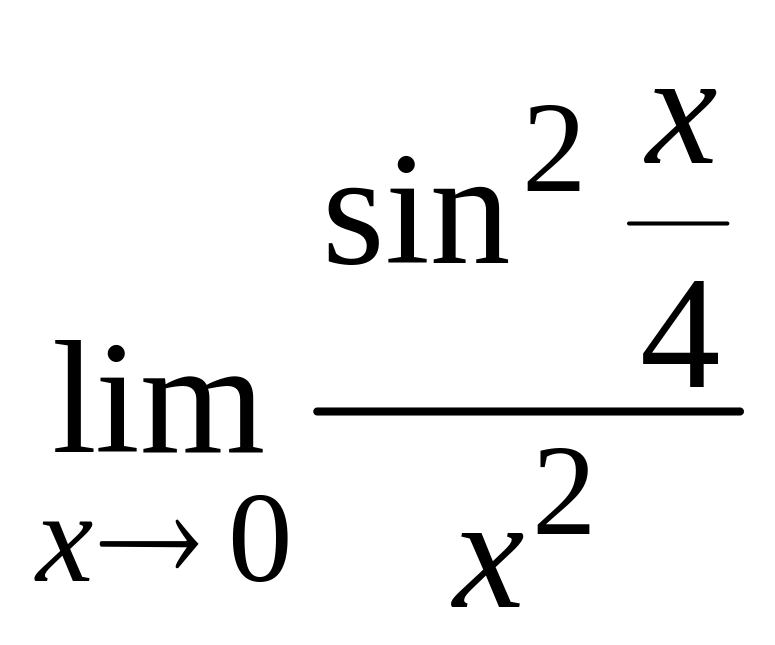 ;
г)
;
г)
![]() .
.
12.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
13.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
14.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
15.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
16.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
17.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
18.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
19.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
20.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Тема 6. Дифференциальное исчисления функций одной переменной.
№9. Найти производные первого порядка данных функций, используя правила вычисления производных.
1.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
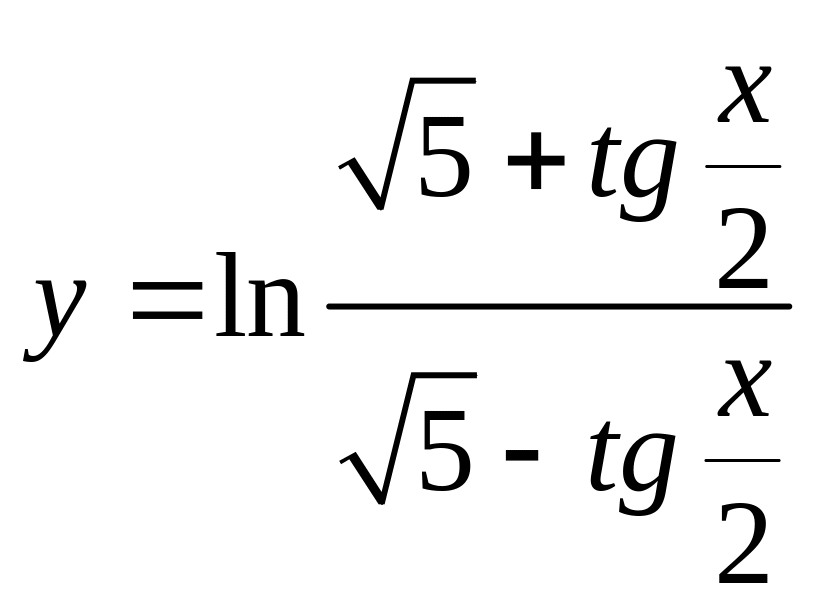 ,
д)
,
д)
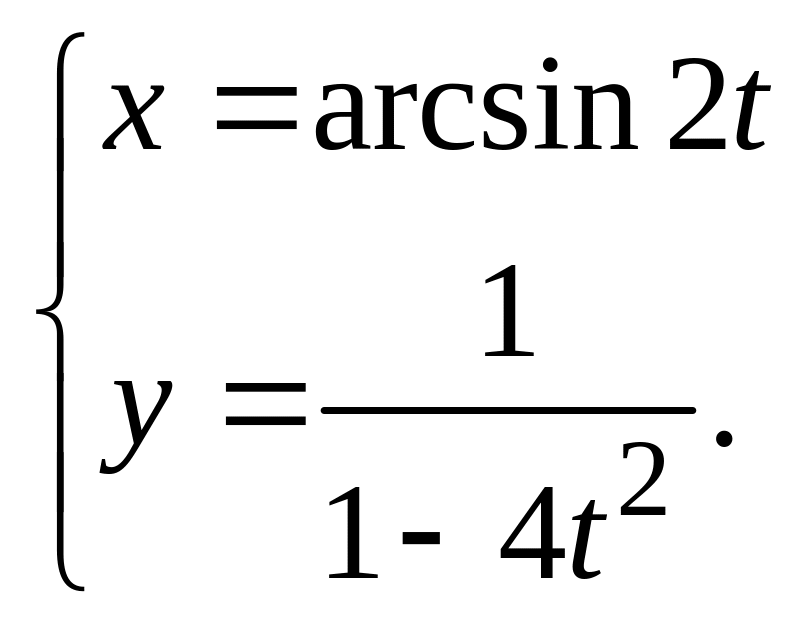
2.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
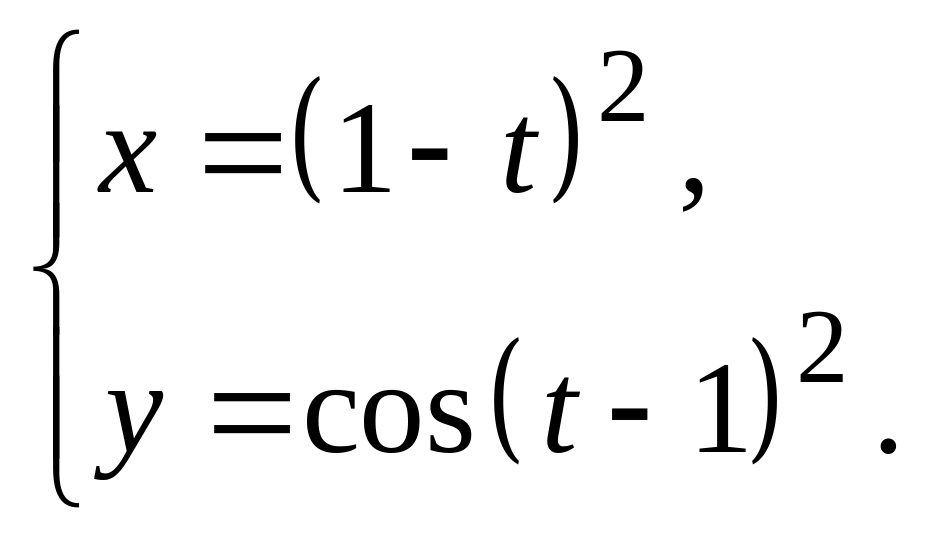
3.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
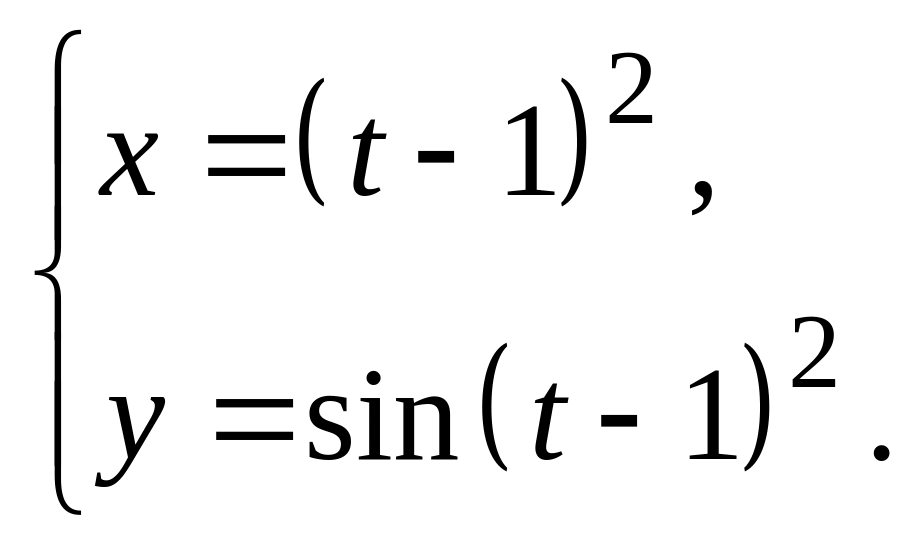
4.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
![]()
5.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
![]()
6.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
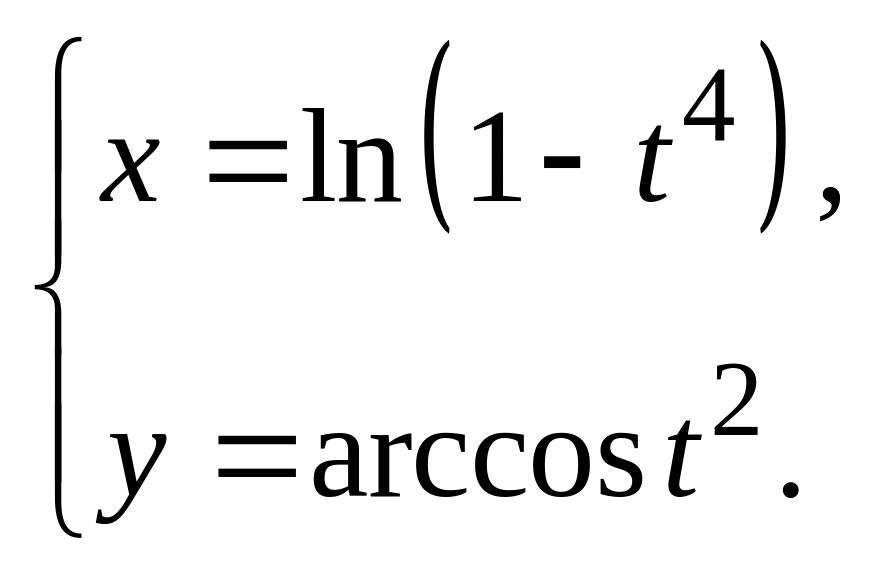
7.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
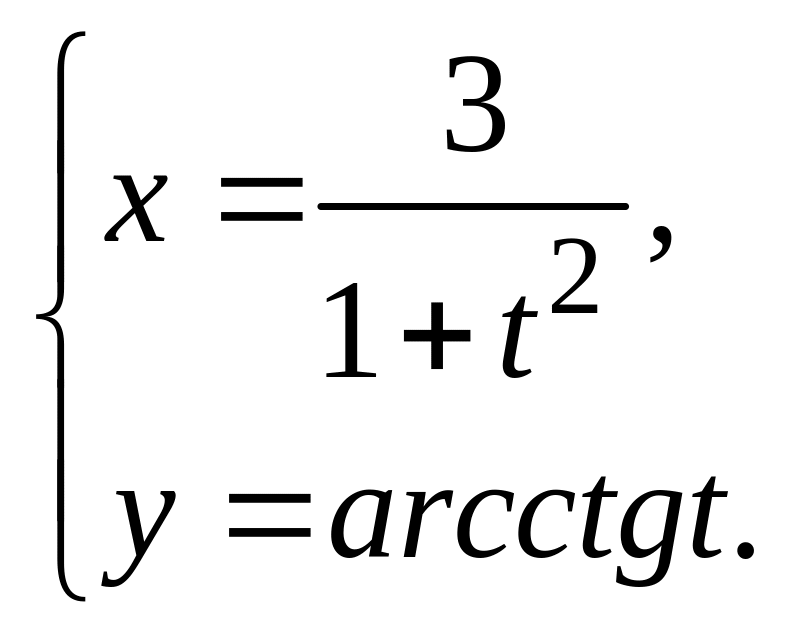
8.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
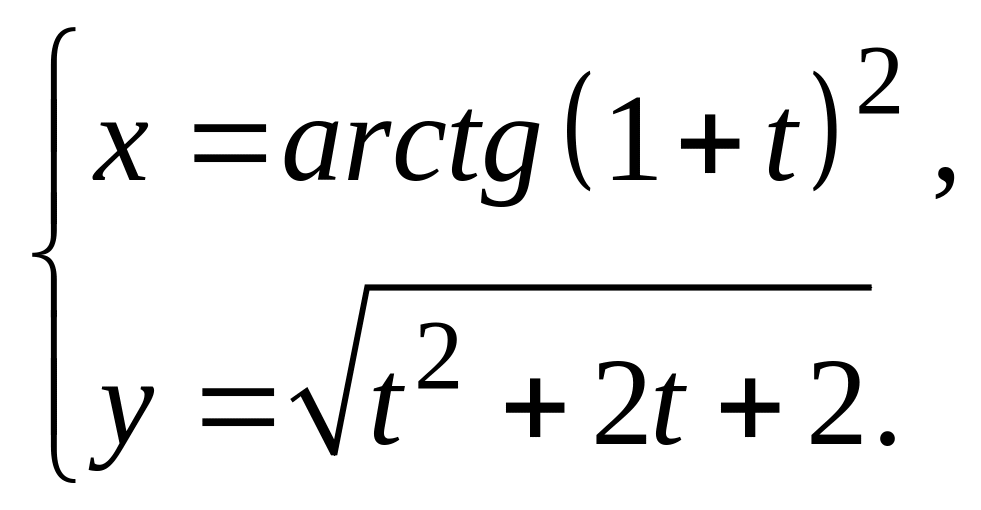
9.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
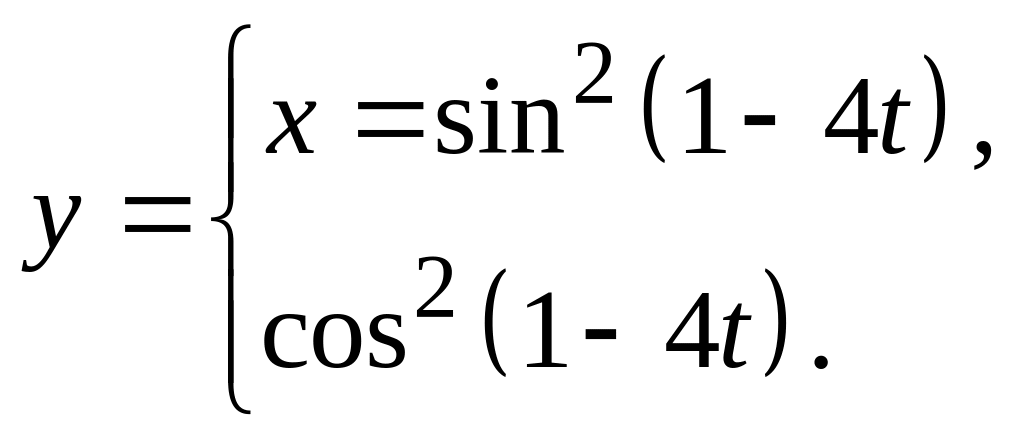
10.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
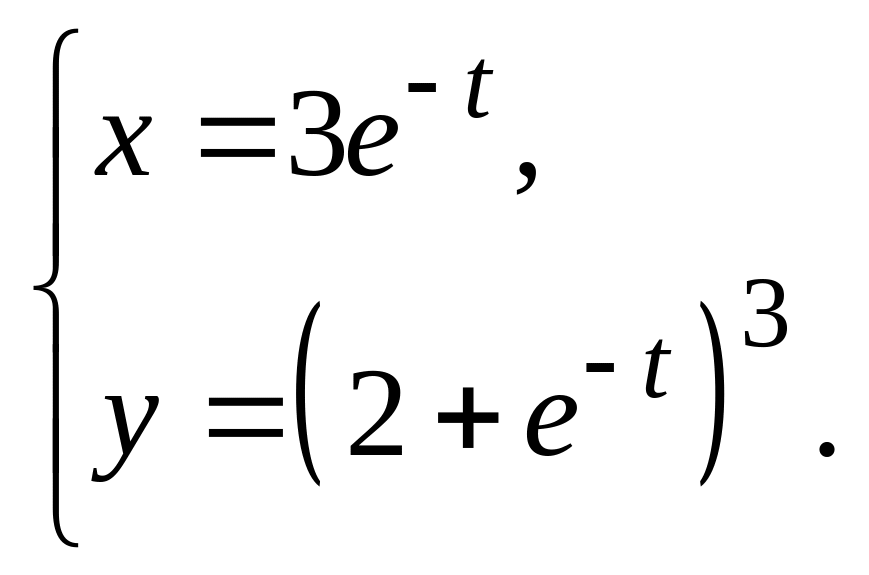
11.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
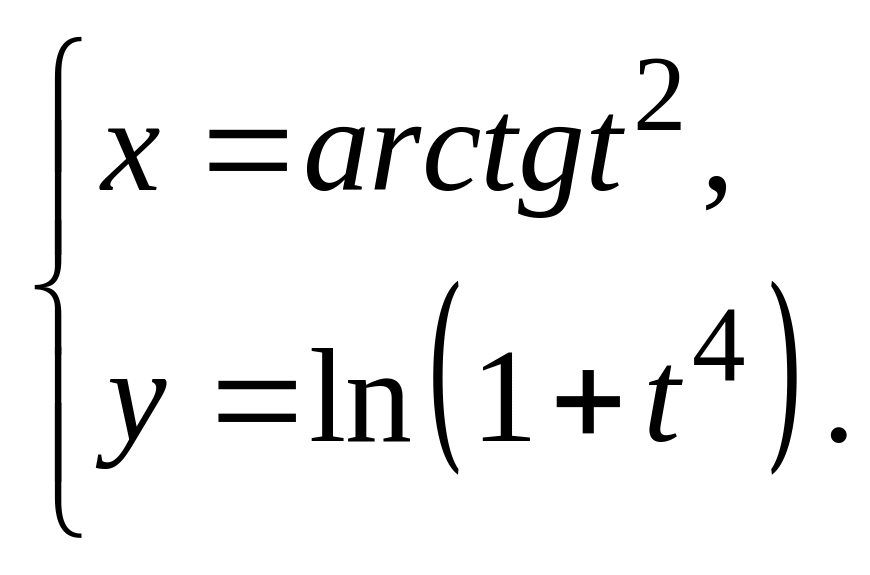
12.
а)
![]() б)
б)
![]() в)
в)![]()
г)
![]() ,
д)
,
д)
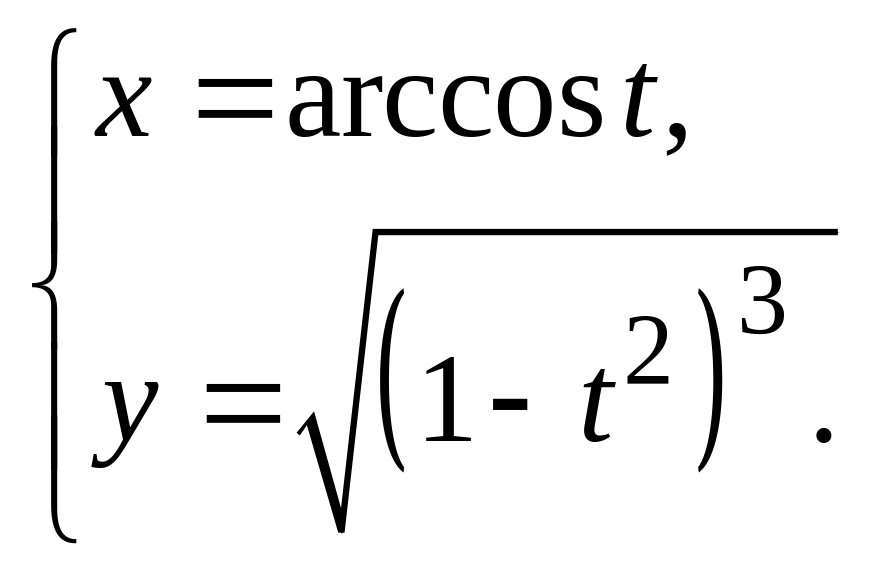
13.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
![]()
14.
а)
![]() б)
б)
![]() в)
в)![]()
г)
![]() д)
д)
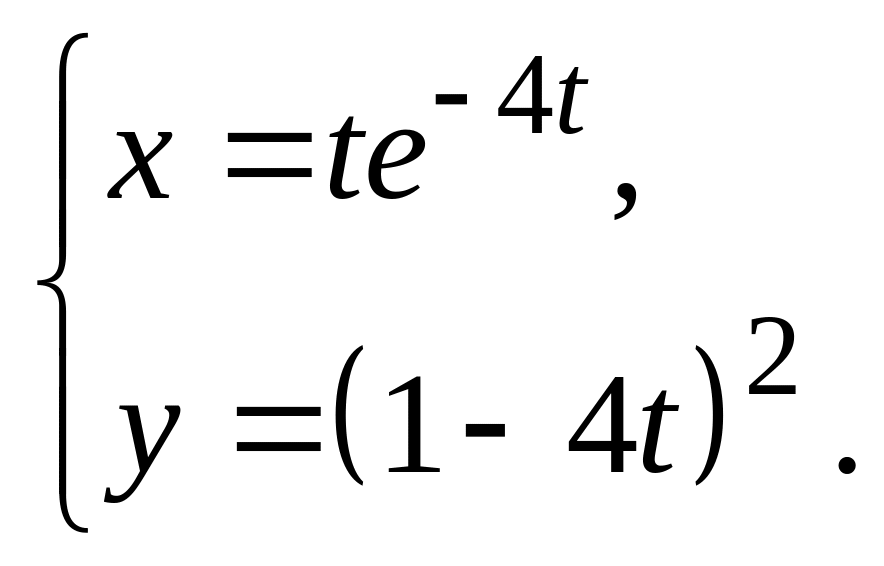
15.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
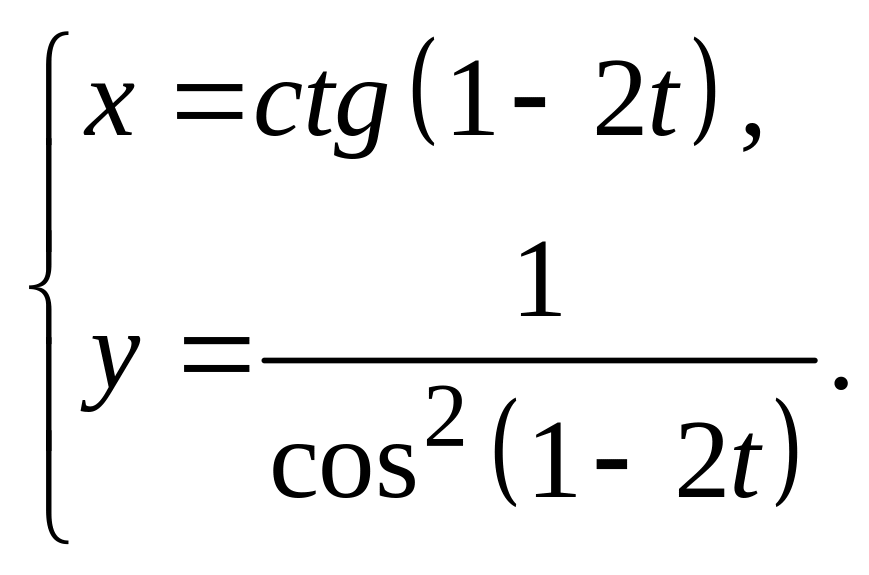
16.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
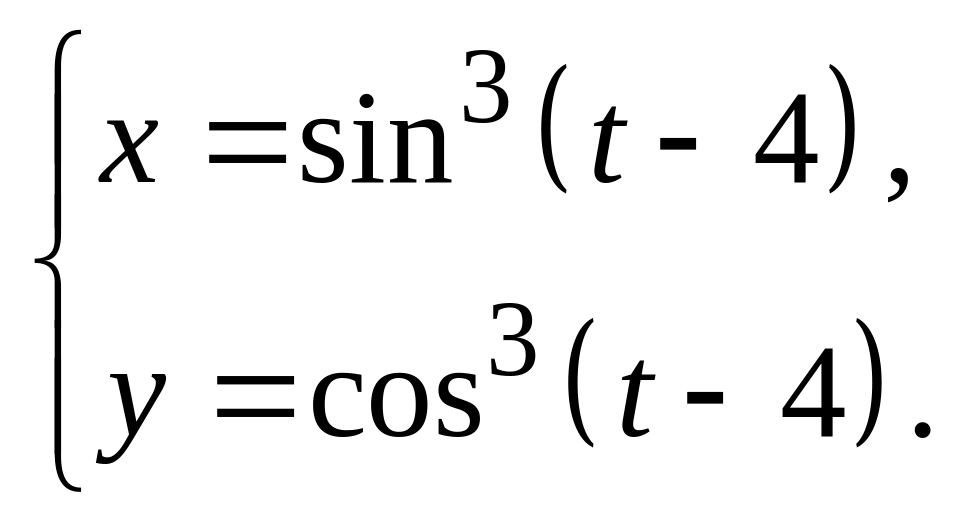
17.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
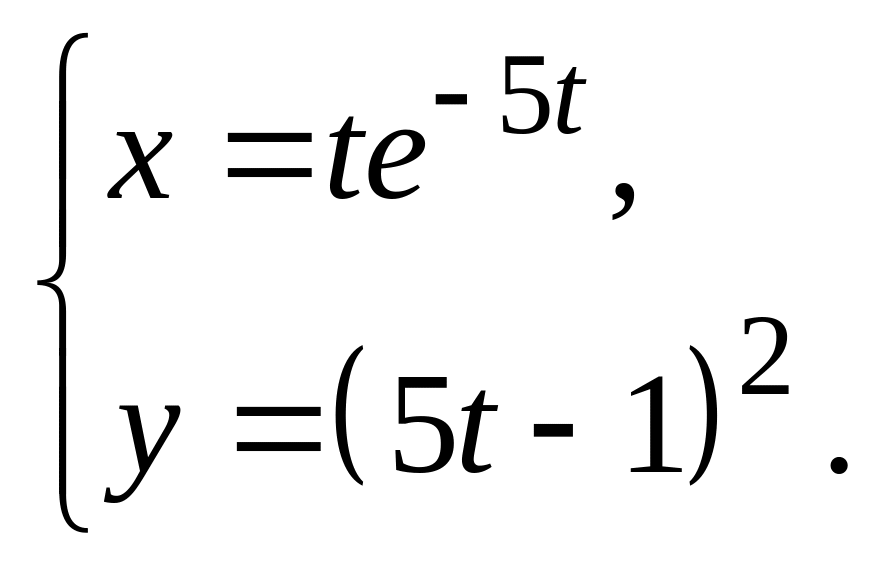
18.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)

19.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() ,
д)
,
д)
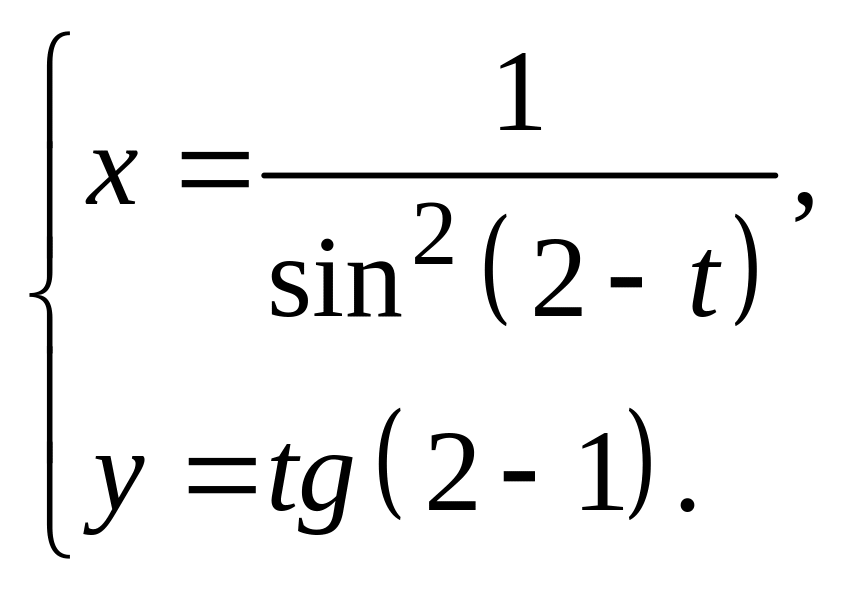
20.
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
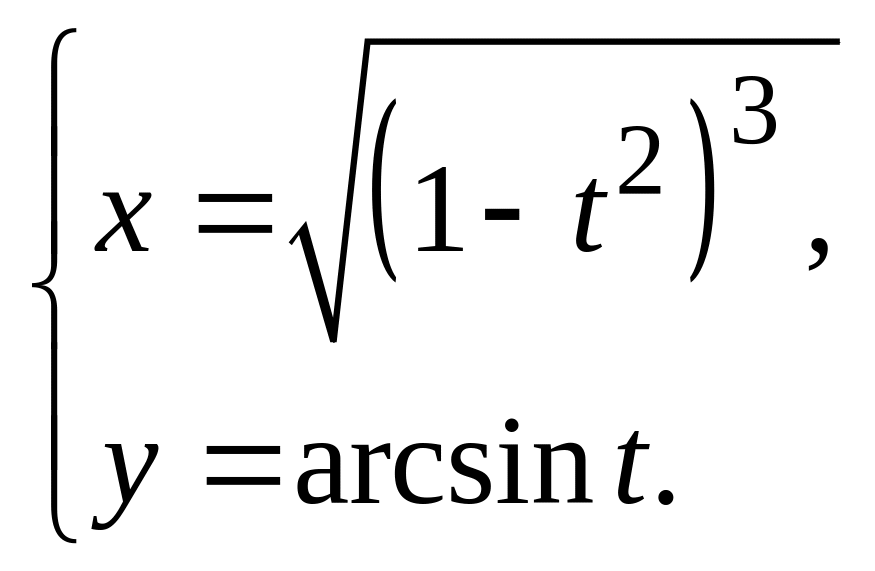
№10. Вычислить предел функции с помощью правила Лопиталя.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
№11. Построить график функции , используя общую схему исследования.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
