1.2. Фильтр верхних частот

АЧХ идеального фильтра верхних частот (ФВЧ) имеет вид

и характеризуется только нижней частотой среза _н. Поскольку АЧХ реального ФВЧ является плавной функцией частоты, в качестве _н реального ФВЧ берут частоту, на которой АЧХ уменьшается в раз по сравнению с ее значением k() , то есть

.

(4)

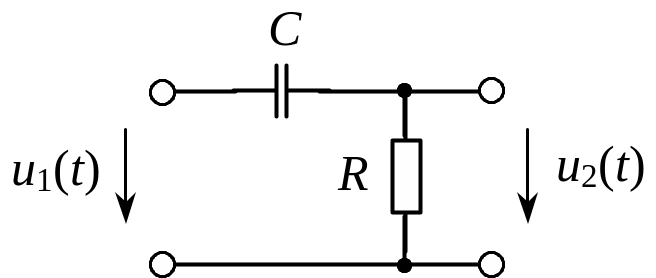
В качестве простейшего ФВЧ может использоваться дифференцирующая RC-цепь (рис. 3). АЧХ этой цепи определяется выражением

(5)

и показана на рис. 4. Частота среза этого фильтра равна _н = 1/RC.

1.3. Полосовой фильтр

Идеальный полосовой фильтр (ПФ) обладает АЧХ следующего вида

причем k(0) = k() = 0.

АЧХ реального полосового фильтра напоминает резонансную кривую с ярко выраженным максимумом. Частота, на которой достигается максимум частотной характеристики фильтра, называется его резонансной частотой ₀, а нижняя и верхняя частоты среза определяются исходя из равенства

.

(6)

Величина Q = ₀/(_в – _н) называется добротностью полосового фильтра.

Рис. 5. Полосовой фильтр на основе ФНЧ и ФВЧ

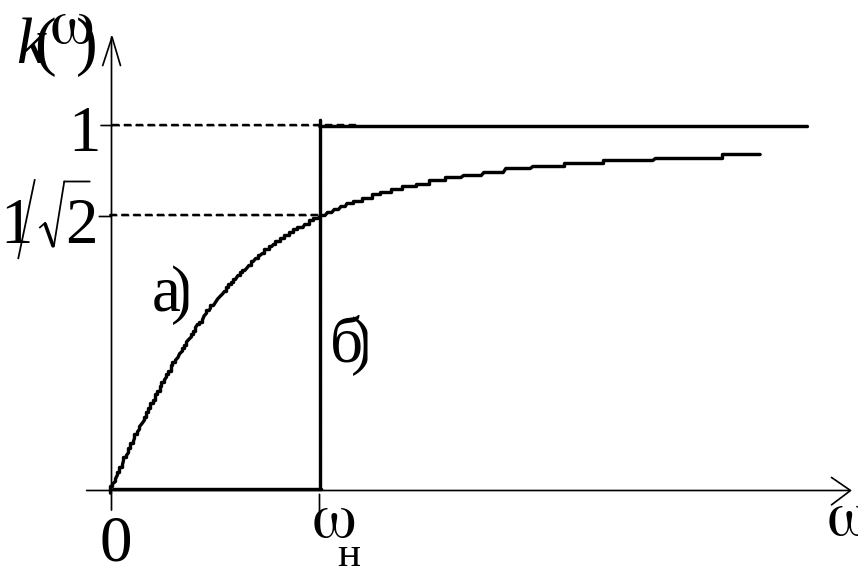
Рис. 4. АЧХ реального (а) и идеального (б) ФВЧ

Рис. 3. RC-фильтр верхних частот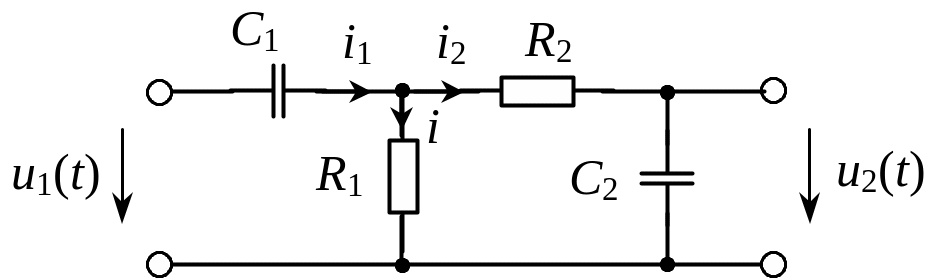

Рассмотрим варианты реализации пассивных ПФ. Простейший вариант полосового фильтра можно получить, соединив последовательно рассмотренные выше ФВЧ и ФНЧ (рис. 5). Однако частотная характеристика получившейся схемы не будет являться произведением частотных характеристик исходных фильтров, поскольку второй фильтр является нагрузкой для первого. Вычислим частотную характеристику ПФ методом комплексных амплитуд, записав несколько очевидных соотношений:

.

Решение этих уравнений относительно входного и выходного напряжений дает выражение для частотной характеристики:

,

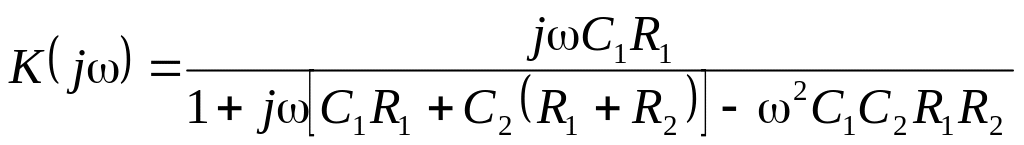которой соответствует АЧХ вида

.

(7)

Видно, что k(0) = k() = 0, а резонансная частота фильтра определяется выражением

.

Однако чаще в качестве полосового фильтра используют фильтр Вина, схема которого приведена на рис. 6. Его частотная характеристика определяется выражением

,

а АЧХ равна

.

(8)

Пользуясь выражениями (6) и (8) и определением резонансной частоты, найдем параметры фильтра Вина

.

АЧХ фильтра Вина и идеального полосового фильтра приведены на рис. 7. Заметим, что хотя в этой схеме сопротивления резисторов R и емкости конденсаторов C предполагаются равными, их небольшой разброс практически не влияет на значения частот среза фильтра, а лишь несколько смещает резонансную частоту и изменяет максимальное значение АЧХ.

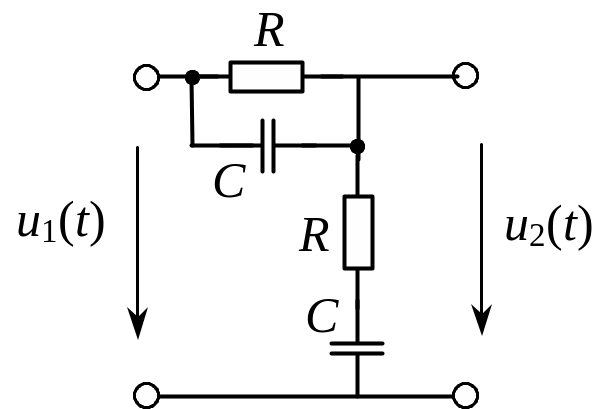
Рис. 6. Полосовой фильтр Вина		Рис. 7. АЧХ фильтра Вина (а) и идеального полосового фильтра (б)

1.4. Режекторный фильтр

АЧХ идеального режекторного фильтра (РФ) имеет следующий вид

причем k(0) = k() = k_max = 1. АЧХ реального РФ так же, как и ПФ может характеризоваться резонансной частотой, на которой достигается минимум частотной характеристики фильтра k_min, а нижняя и верхняя частоты среза определяются исходя из равенства

.

(9)

Величина Q = ₀/(_в – _н) называется добротностью РФ, а отношение  = k_max/k_min – глубиной режекции.

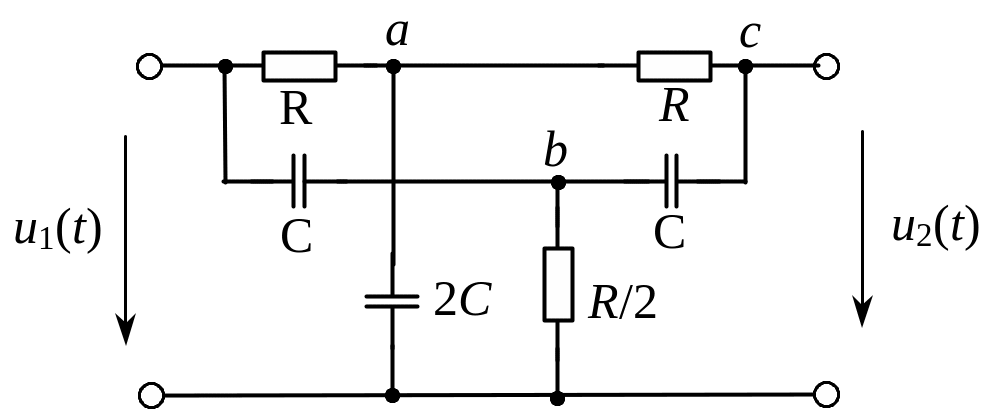
Существует несколько вариантов реализации пассивных режекторных RC-фильтров. Так, например, в качестве РФ можно использовать обратный фильтр Вина (рис. 8). Однако коэффициент режекции данной схемы невелик, поэтому чаще в качестве РФ используют мост Вина–Робинсона (рис. 9) или двойной Т-образный фильтр (рис. 10). Заметим, что входное и выходное напряжения моста Вина–Робинсона не имеют общего зажима, в отличие от двойного Т-образного фильтра. Поскольку в данной лабораторной работе используется именно последняя схема, приведем расчет ее частотной характеристики в рамках методов комплексных амплитуд и узловых потенциалов.

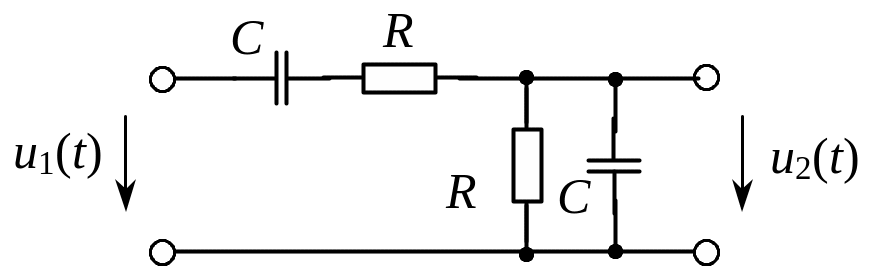
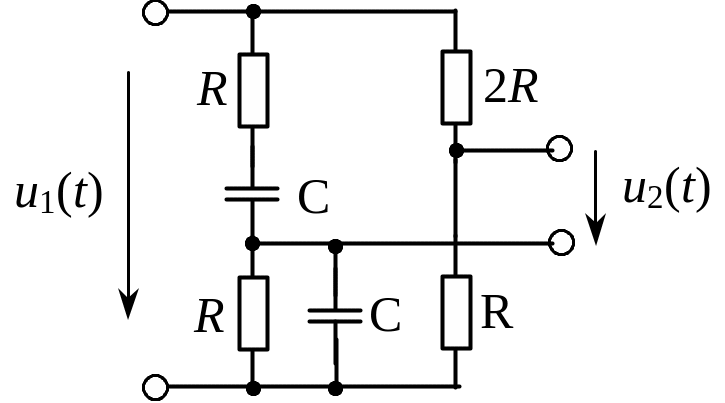
Рис. 8. Режекторный фильтр Вина		Рис. 9. Мост Вина–Робинсона

Рис. 10. Двойной Т-образный фильтр

Запишем уравнения Кирхгофа для узлов a, b и c, обозначив их потенциалы и соответственно:

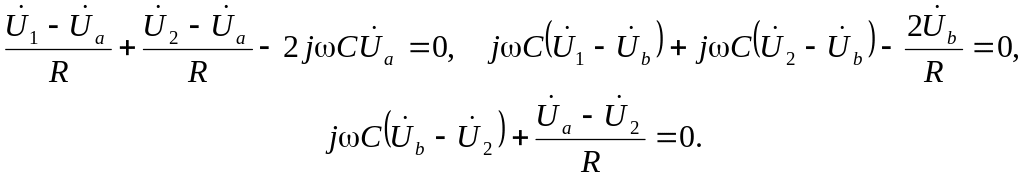
Исключая из этих уравнений потенциалы и , получим частотную характеристику двойного Т-образного фильтра

и его АЧХ

.

(10)

Сравнивая выражения (9) и (10), а также используя определение добротности, получим значения основных параметров РФ:

.

Значение коэффициента режекции данного фильтра стремится к бесконечности, однако это выполняется только при абсолютном равенстве сопротивлений резисторов R и емкостей конденсаторов C.

Заканчивая описание пассивных RC-фильтров, отметим, что все полученные нами частотные характеристики найдены для ненагруженных фильтров.
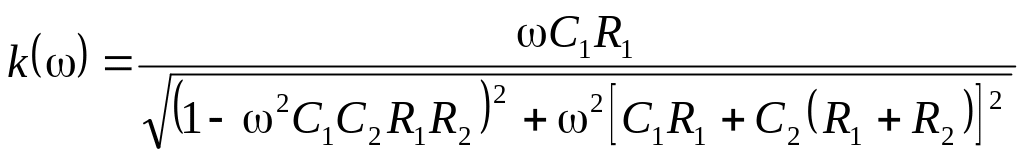