4.3 Реализация цф в виде подпрограмм

Так как ранее были выбраны 10-разрядные АЦП и ЦАП, то и могут принимать значения 0-1023. Это соответствует точности преобразования 0,1% от максимальной величины сигнала.

Для хранения 10-разрядных величин и коэффициентов, выделим в ОЗУ по два байта. Ввод значений осуществляется микропроцессором с аналого-цифрового преобразователя побайтно. После ввода каждого нового значения необходимо записать его в ОЗУ, вычислить управляющее воздействие , выдать его на ЦАП, переместить величину на место , а - на место . После этого процессор готов к вводу нового значения .

Для уменьшения объема ПЗУ, занятого программами, умножение, деление и сложение реализуется в виде подпрограмм.

ЦФ также реализуется в виде подпрограмм. Это позволяет применять их как в единой измерительной системе, так и отдельно. Подпрограммная реализация ЦФ позволяет использовать различную организацию микропроцессорной системы (одно- или многопроцессорную).

Дифференцирующее звено.

Разностное уравнение можно записать в виде:

где

Т.к. в ОЗУ записываются целые числа, а <1, то целесообразно заносить в память . Для того, чтобы это не повлияло на результат, произведение затем делится на 10. С учетом этого уравнение запишется:

Перед началом работы подпрограммы должны быть записаны в ОЗУ (рисунок 4.7).

Рисунок 4.7.

После записи с АЦП, указатель стека (SP) устанавливается на мл.байт .

Корректирующий дифференцирующий фильтр.

Его разностное уравнение перепишется в виде:

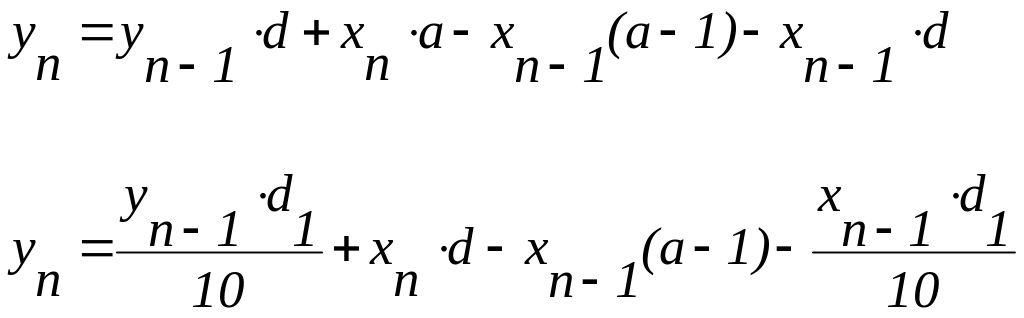
где

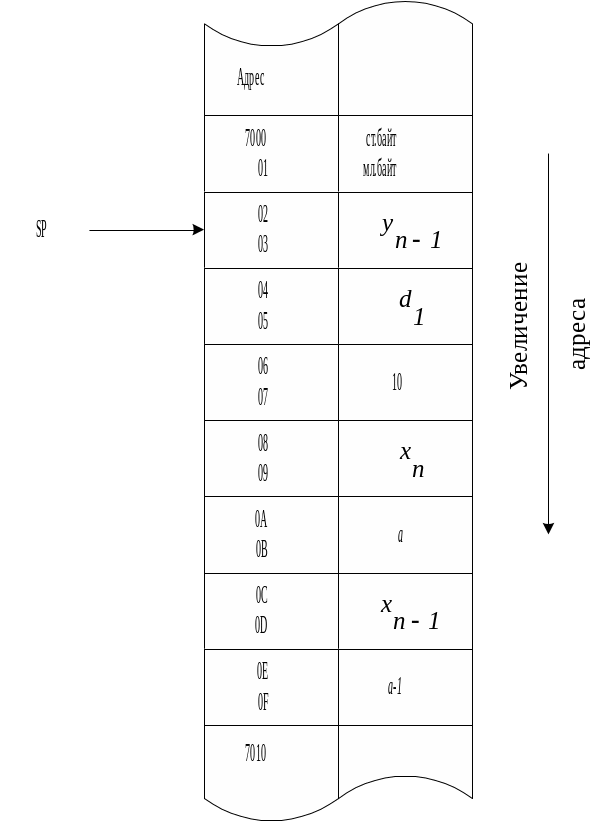
Рисунок 4.8.

Для работы программы данные заносятся в ОЗУ, в порядке указанном на рисунок 4.8.

Результат накапливается в ячейках ОЗУ 7002-7003 вместо .

После вычислений, записывается на место . А в ячейки 7008-7009 записывается новое значение при последующем цикле вычислений.

Корректирующий интегро-дифференцирующий фильтр, корректирующий фильтр с повышением порядка астатизма.

Так как разностное уравнение у обоих фильтров одинаково, очевидно, что и программная реализация их будет одна и та же. Разница лишь в числовых значениях коэффициентов.

Разностное уравнение можно переписать как:

Для того, чтобы избавиться от знаменателя, можно было бы коэффициенты при и разделить на е. Но это нецелесообразно, т.к. получатся дробные коэффициенты.

Для работы программы, и постоянные коэффициенты записываются в ОЗУ (рисунок 4.9).

Рисунок 4.9.

Для того, чтобы коэффициенты были положительными, в ОЗУ записываются -f, -g и -e.

Сумма накапливается в ячейках памяти 7100-7101, а после деления на -e результат заносится на место . Одновременно из этой ячейки извлекается . Затем заносится в ячейки 7106-7107 с одновременным извлечением из них . Аналогично переписываются и значения .

Лекция 5 анализ и синтез дискретных су

5.1 Обеспечение заданной точности

Частотные характеристики импульсных и цифровых систем в области низких частот для значений , где Т-период дискретности, практически совпадают с частотными характеристиками непрерывной части разомкнутого канала, это оказывается справедливым для цифровых систем при линеаризации задачи и в предположении, что передаточная функция самой цифровой машины D(z)=l или, в общем случае, D(z)== const.

Кроме того, следует заметить, что для обеспечения необходимого запаса устойчивости приходится всегда выбирать желаемую л.а.х., чтобы удовлетворялось условие , где - частота среза л.а.х.

В связи с этим на импульсные и цифровые системы можно распространить правила построения запретной области для л.а.х.

Рис.5.1. Запретная область для л.а.х.

Эта область практически построена в функции псевдочатоты . Для частот меньших, чем частота среза, , псевдочастота практически совпадает с обычной круговой частотой, .

Частота контрольной точки определяется формулой

, (5.1)

где , - максимальные значения скорости и ускорения воздействия g(t), действующего на входе.

Базовая частота

, (5.2)

где - добротность по ускорению, а - максимально допустимое значение ошибки.

Аналогичным образом могут быть построены запретные области других видов. При действии на входе случайных сигналов могут быть сформулированы требования к низкочастотной части л.а.х.

Рассмотрим влияние периода дискретности. Наличие квантования по времени в дискретных системах может вызвать потерю информации об изменении входной величины внутри интервала дискретности, что приводит к появлению дополнительной ошибки. Рассмотрим этот вопрос более подробно.

Пусть r - порядок астатизма исходной системы, а l - порядок экстраполятора (в импульсных системах l=-1). Покажем, что порядок используемого экстраполятора не влияет на результирующий порядок астатизма дискретной системы. Для этого рассмотрим дискретную передаточную функцию разомкнутой системы при t  , т.е. при р  0:

(5.3)

Здесь - общий коэффициент усиления системы с астатизмом r-го порядка. Из формулы 5.3 видно, что астатизм системы с экстраполятором 1-го порядка остался равным r.

Рассмотрим теперь влияние астатизма системы на порядок экстраполяции. Пусть входной сигнал меняется по закону

(5.4)

Тогда при k<r установившаяся ошибка системы управления , а при k=r, ошибка . Первые r-1 коэффициентов ошибки при этом равны нулю, т.е. (i=0,l,...,r-l). Следовательно, накапливающаяся ошибка на выходе экстраполятора 0-го порядка (1=0), при будет равна нулю.

Накапливающаяся ошибка на выходе экстраполятора 1-го порядка (1=1) будет равна 0, если , что соответствует k=r+l. Накапливающаяся ошибка на выходе экстраполятора 2-го порядка (1=2) накапливающаяся ошибка будет отсутствовать при изменении ошибки по закону , что допускает значение k=r+2.

Продолжая эти рассуждения, получаем, что на выходе экстраполятора 1-го порядка будет отсутствовать накапливающаяся ошибка, если

, (5.5)

где m=l+r - порядок экстраполяции системы, равный сумме порядка используемого экстраполятора и порядка астатизма исходной ситемы.

Это означает, что накапливающаяся ошибка на выходе экстраполятора может вызываться входным воздействием вида (5.4) при k>m=l+r.

Так как в дискретные моменты времени t=nT накопившаяся на выходе экстраполятора ошибка сбрасывается, то формула для накапливающейся ошибки внутри такта может быть представлена в виде

. (5.6)

Максимум ошибки будет в конце такта, при t=(n+l)T:

. (5.7)

Отсюда может быть найдено допустимое значение периода дискретности при заданном значении :

. (5.8)

В качестве величины должно выбираться максимальное значение производной (m+1)-го порядка от входной величины g(t).

Если входное воздействие представляет собой гармоническую функцию , то предыдущая формула приобретает следующий вид:

. (5.9)

Формулы 5.8 и 5.9 позволяют выбирать период дискретности Т из условия ограничения накапливающейся ошибки.

Так, например, если r=1 и 1=0, то m=1 и допустимое значение периода дискретности определяется максимальным значением ускорения на входе:

. (5.10)