
Лекція 16
Тверде тіло
Класична теорія теплоємності твердих тіл. Недоліки класичної теорії.
Квантова теорія теплоємностей Ейнштейна. Недоліки теорії Ейнштейна.
Теплове розширення тіл.
Дифузія в твердих тілах.
Фазові переходи 1- та 2-го роду. Рівняння Клапейрона-Клаузіуса.
Література: [1] стор. 321-334, [2] стор. 459-465, [7] стор. 224-232
Сформулюйте закон Дюлонга і Пті. Як отримати цей закон на основі класичної теорії теплоємностей? Які труднощі виникають в цій теорії при її застосуванні до металів?
В чому суть основної ідеї квантової теорії теплоємності твердих тіл?
В чому принциповий недолік моделі Ейнштейна для теплоємності твердого тіла?
Що таке фонон? Які інші елементарні збудження ви знаєте?
Модель Дебая.
Література: [1] стор. 383-386, [2] стор. 473-476
В чому головна відмінність механізму переносу в твердих тілах і рідинах від механізму переносу в газах?
Вкажіть три способи реалізації дифузії в твердих тілах. Якого порядку коефіцієнт дифузії в твердих тілах?
З яких величин складається енергія активації дифузії?
Література: [1] стор. 293-297, 334-343 [2] стор. 436-454, [7] стор. 443-455,
Дайте визначення і наведіть приклади фазових переходів 1 і 2-го роду.
Розкажіть про фазові перетворення речовин і накресліть відповідні криві фазових рівноваг в діаграмі Т – Р.
1. Класична теорія теплоємностей твердих тіл
Уявимо
собі кристал з N
атомів, які здійснюють коливання біля
положення рівноваги, що визначається
мінімумом потенціальної енергії. Згідно
теорії про рівнорозподіл середньої
енергії по ступеням вільності, на кожну
трансляційну та кожну обертальну ступені
вільності приходиться середня кінетична
енергія
![]() ,
на кожну коливальну ступінь вільності
енергія
,
на кожну коливальну ступінь вільності
енергія
![]() .
Кожен атом має три коливальні ступені
вільності. Моль твердого тіла матиме
внутрішню енергію
.
Кожен атом має три коливальні ступені
вільності. Моль твердого тіла матиме
внутрішню енергію
![]()
 .
(1)
.
(1)
А молярна теплоємність твердого тіла
молярна теплоємність твердого тіла
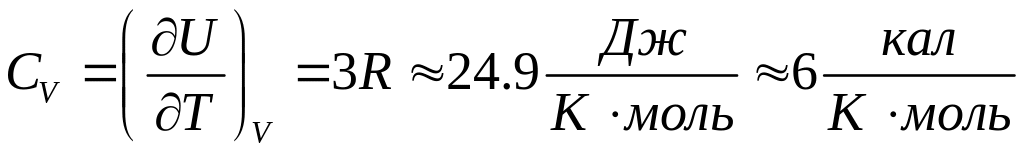 .
(2)
.
(2)
Це відомий закон
Дюлонга і Пті: добуток питомої
теплоємності хімічного елемента в
твердому стані на його атомну масу
приблизно однаковий для всіх елементів
і складає приблизно
![]() .
І, як бачимо, цей закон знаходить своє
пояснення в рамках класичної теорії
теплоємностей і мова йдеться про молярну
теплоємність при постійному об’ємі. В
таблиці представлені теплоємності
деяких елементів в твердому стані в
температурному інтервалі від 15 до 100 С
.
І, як бачимо, цей закон знаходить своє
пояснення в рамках класичної теорії
теплоємностей і мова йдеться про молярну
теплоємність при постійному об’ємі. В
таблиці представлені теплоємності
деяких елементів в твердому стані в
температурному інтервалі від 15 до 100 С
Елемент |
|
Елемент |
|
C |
1.44 |
Pt |
6.11 |
B |
2.44 |
Au |
5.99 |
Al |
5.51 |
Pb |
5.94 |
Ca |
5.60 |
U |
6.47 |
Ag |
6.11 |
|
|
Теорему
про рівнорозподіл енергії по ступеням
вільності можна застосувати і до твердих
тіл, які являють собою хімічні сполуки.
В цьому випадку моль речовини буде
містити в n
разів більше гармонічних осциляторів,
і, відповідно, молярна теплоємність
![]() .
Молярна
теплоємність твердої сполуки рівна
сумі молярних теплоємкостей елементів,
із яких вона складається.
.
Молярна
теплоємність твердої сполуки рівна
сумі молярних теплоємкостей елементів,
із яких вона складається.
Це правило було вперше висловлено Джоулем в 1844 р. і остаточно сформульовано і обґрунтовано великою кількістю дослідних даних в 1864 р. Коппом.
Недоліки класичної теорії теплоємностей.
1. Існує ряд дослідних фактів, які класична теорія поясніть не може.
Теплоємність
твердих тіл залежить від температури.
При наближенні до абсолютного нуля
теплоємності
![]() і
і![]() всіх тіл прямують нуля.
всіх тіл прямують нуля.
Можна було б спробувати пояснити теплоємності від температури негармонічністю коливальних ступенів вільності при великих амплітудах коливань. Для негармонійних коливань середня кінетична енергія, що приходиться на одну ступінь вільності, вже не дорівнює відповідній середній потенціальній енергії. Співвідношення між ними залежить від амплітуди коливань, тобто і від температури речовини. В цьому випадку пояснюється зміна теплоємності із зростанням температури. Але при низьких температурах, згідно класичним уявленням, амплітуди коливань малі і в більшій мірі відповідають гармонійним.
2. Класична теорія непослідовна.
Теорема
про рівнорозподіл енергії на виділяє
ступені вільності, тобто кожній ступені
вільності приписується одна і та ж
частина середньої кінетичної енергії.
Між тим при розрахунках теплоємності
речовини одні ступені вільності
враховується, а інші не приймаються до
уваги. Так класична теорія теплоємності
одноатомних газів досягає узгодженості
із дослідом, коли розглядає атом як
матеріальну точку із трьома ступенями
вільності. Але атом не є матеріальною
точкою. Якщо його вважати твердим тілом,
то необхідно йому приписати шість
ступенів вільності, а теплоємність
одноатомного газу буде складати
![]() .
Між тим атом не являється твердим тілом,
а має складну внутрішню будову і число
ступенів вільності набагато більше
шістьох. Тобто при послідовному розгляді
теплоємність одноатомного газу за
класичною теорією повинна бути на багато
більша, ніж
,
що протирічить фактам.
.
Між тим атом не являється твердим тілом,
а має складну внутрішню будову і число
ступенів вільності набагато більше
шістьох. Тобто при послідовному розгляді
теплоємність одноатомного газу за
класичною теорією повинна бути на багато
більша, ніж
,
що протирічить фактам.
3.
Класична теорія не може пояснити, чому
для знаходження теплоємності, наприклад
молекулярного водню при низьких
температурах, необхідно користуватись
моделлю одноатомного газу (![]() ),
при кімнатних – моделлю жорсткої гантелі
(
),
при кімнатних – моделлю жорсткої гантелі
(![]() ),
при дуже високих – моделлю гантелі, в
якій атоми можуть коливатись вздовж
вісі, що з’єднує атоми, (
),
при дуже високих – моделлю гантелі, в
якій атоми можуть коливатись вздовж
вісі, що з’єднує атоми, (![]() ).
).
4. Розглянемо теплоємність металів. В атомі присутні так звані вільні електрони, які досить слабо пов’язані з іонами ґратки, і наявністю яких пояснюється висока електропровідність в металах. Але класична теорія не приймає до уваги наявність вільних електронів. Якщо електрони розглядати матеріальні точки, то теплоємність електронного газу за класичною теорією буде того ж порядку, що і теплоємність ґратки. Однак дослід показує, що і вільні електрони майже не дають вкладу в теплоємність металів.
Перераховані труднощі долаються при послідовній розбудові теорії на квантовій основі.
