19

Глава 2. Моделирование случайных событий

2.1.Единичный жребий

Имитация функционирования стохастической системы на ЭВМ заключается в многократном прогоне модели системы. Результатом однократного прогона является одна реализация моделируемого процесса (явления). Реализация - это один экземпляр процесса. Реализации отличаются друг от друга за счет случайностей. Отдельная реализация случайного явления разыгрывается при помощи специального алгоритма, важную роль, в котором играет процедура "бросания жребия". Каждый раз, когда в ход процесса вмешивается случай, его влияние учитывается не расчетом, а жеребьевкой. Именно этим имитационное моделирование принципиально отличается от аналитического. К жеребьевке в имитационном моделировании прибегают каждый раз, когда дальнейшее развитие процесса (а значит и его результата) зависит от того, произошло или нет какое-то событие. Например, попал ли снаряд в цель, исправна ли аппаратура, устранена ли неисправность и т.п. Кроме случайных событий на ход и исход процесса могут влиять различного рода случайные величины, например, стартовая масса ракеты, толщина листового проката, пределы прочности и др. С помощью жребия можно разыграть значение любой случайной величины, любого случайного вектора.

Жеребьевка при помощи ЭВМ имеет свою специфику. Здесь не пригодны тиражные барабаны, лототроны и даже электронные генераторы из-за их низкой производительности. Для этой цели применяют специальные программные генераторы случайных величин. Величины, получаемые при помощи программы, конечно, не являются действительно случайными, но обладают многими свойствами случайных величин. Поэтому они называются псевдослучайными.

Основой для моделирования случайных событий и случайных величин с различными законами распределения служит базовая случайная величина, равномерно распределенная в интервале (0,1). Программные генераторы псевдослучайных величин используют рекуррентные математические методы, позволяющие каждое новое число получать из одного или нескольких предыдущих.

2.2.Базовая случайная величина

Так называется случайная величина, распределенная равномерно в интервале от 0 до 1. Обозначим ее символом R. Плотность распределения f(r) базовой случайной величины такова

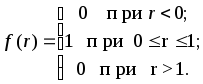
Математическое ожидание и дисперсия базовой случайной величины соответственно равны

M(R)=0.5; D(R) = 1/12.

2.3.Мультипликативный конгруэнтный генератор базовой случайной величины

Два целых числа A и B конгруэнтны (сравнимы) по модулю M, если их разность делится на M без остатка. То есть

A - B = k M,

где k - целое. Это определение записывается так

A = B (mod M).

Основная формула мультипликативного конгруэнтного метода генерирования случайных величин имеет вид:

где a и M положительные целые числа. Согласно этому выражению, для получения очередного числа следует взять последнее число, умножить его на постоянный множитель a, разделить на M и остаток приравнять. Иначе

(2.1)

где k выбирается так, чтобы

В алгоритмических языках программирования (Фортран, Паскаль) существует встроенная функция mod, выполняющая эту операцию.

График функции (2.1) изображен на рис. 2.1. От выбора a и M зависят статистические свойства программы - генератора. В качестве модуля M обычно выбирают максимально возможное целое число. При 32-разрядном двоичном коде это число равно Такой выбор обеспечивает наибольший период. Хорошие статистические свойства последовательности псевдослучайных чисел обеспечивается выбором a и стартового числа. Множитель a не должен быть каким-либо образом связан с модулем M. При

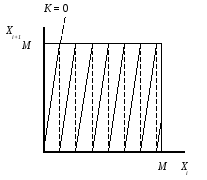
Рис. 2.1.

указанном значении M хорошие результаты получаются со следующими a: 16807, 477 211 307, 1 220 703 125, 6 469 693 231. В качестве следует использовать большое целое нечетное число.

Для того чтобы из получить величину, заключенную в интервале (0,1) достаточноразделить на модуль M. Наиболее распространенная программа-генератор (на Фортране) значений базовой псевдослучайной величины выглядит так.

Subroutin Randu (ix, iy, R)

iy = ix * 1 220 703 125

If (iy) 3, 4, 4

3 iy = iy + 2 147 483 647 + 1

4 R = iy * 0.4656613e-9

Return

End

Кроме рассмотренного применяются и другие более сложные генераторы, например, конгруэнтный аддитивный, использующий правило

Статистические свойства генераторов псевдослучайных величин проверяются при помощи многочисленных тестов. Так для проверки равномерности распределения единичный квадрат (куб, гиперкуб) разбивается (произвольно) на m частей с площадями (объемами) , так что сумма площадей равна единице. Затем генерируется 2N (в случае квадрата) чисел, из которых образуется N пар

Каждая пара представляет собой точку в квадрате. Если в каждой части квадрата окажется точек, частоты попадания точек равны

Принадлежность частот q распределению p проверяется одним из критериев согласия, например, критерием Пирсона.

Для проверки независимости друг от друга последовательно сгенерированных чисел, вычисляется оценка ковариации лага s:

Эта оценка должна мало отличаться от нуля для всех s, кроме s=0. Для больших N с вероятностью 99.73% статистика

Z = 0.5 ln((1 + K)/(1 - K))

должна быть заключена в интервале