73

Глава 7. Непрерывные цепи Маркова

7.1. Уравнения Колмогорова

Начнем с примера. Техническое устройство ТУ (например, станок-автомат) подвергается простейшему потоку отказов с интенсивностью . Отказ обнаруживается не сразу, а через случайное время, распределенное показательно с параметром . Как только отказ обнаружен, производится осмотр ТУ, в результате которого он либо отправляется в ремонт (вероятность этого p), либо списывается и заменяется новым. Время осмотра показательное с параметром , время ремонта и время замены, тоже показательные с параметрами  и  соответственно.

Возможные состояния ТУ изображены на графе рис.7,1:

s₀ - ТУ исправно,

s₁ - ТУ неисправно, но отказ не обнаружен, производится брак,

s₂ - неисправность обнаружена, ведется осмотр,

s₃ -ТУ ремонтируется,

s₄ - ТУ заменяется новым.





Рис. 7.1.

В отличие от примера с эскадрой в данном случае время должно рассматриваться как непрерывная переменная, а вероятность перехода системы в новое состояние, зависящей от длительности промежутка времени между переходами. Поэтому вместо условной вероятности перехода в подобных случаях вводится плотность вероятности ij, которая определяется как предел отношения вероятности перехода за малый промежуток времени , примыкающий к моменту времени t, к длине этого промежутка, когда он стремится к нулю:

(7.1)

При рассмотрении процессов в системах с дискретными состояниями и непрерывным временем удобно представлять переходы системы из состояния в состояние как происходящие под влиянием некоторых потоков событий, и, следовательно, плотности условной вероятности переходов получают смысл интенсивностей соответствующих потоков событий. Если все эти потоки пуассоновские (ординарные и не имеющие последействия), то процесс, протекающий в системе, будет марковским. В примере с ТУ в качестве таких интенсивностей выступают:

Для описания процесса, протекающего в системе - ТУ, введем вероятности состояний

Рассмотрим состояние s₀. В момент времени t вероятность этого состояния p₀(t). Дадим времени малое приращение t и найдем p₀(t+t). В момент t+t ТУ может оказаться в состоянии s₀ тремя различными способами:

а) в момент t ТУ находилось в этом состоянии и за время t не вышло из него; вероятность этого равна

б) в момент t ТУ находилось в состоянии s₃ и за время t перешло в s₀; вероятность этого равна

в) в момент t ТУ находилось в состоянии s₄ и за время t перешло в s₀; вероятность этого равна

Итак, Отсюда

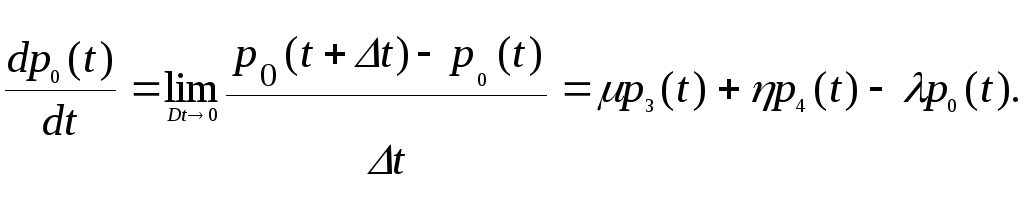
Рассмотрев аналогичным образом остальные состояния ТУ, получим следующую систему уравнений.

(7.2)

Приведенные рассуждения легко распространить на общий случай системы с конечным числом m дискретных состояний и непрерывным временем (см. рис.7,2):

(7.3)

Эта система называется системой уравнений Колмогорова. Уравнения Колмогорова удобно составлять, используя граф состояний. Назовем произведение потоком вероятности перехода из состояния s_i в состояние s_j.

. . .

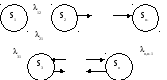
Рис. 7.2.

Тогда можно сформулировать следующее правило: производная вероятности каждого состояния системы равна сумме всех потоков вероятности, идущих из других состояния в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие.

Так как для любого момента времени выполняется условие нормировки

(7.4)

то одно из уравнений 7,2 (любое) должно быть заменено этим равенством.

Чтобы решить систему (7,2) нужно, конечно, иметь начальное распределение вероятностей

Если, в частности, при t = 0 состояние системы в точности известно, например, а вероятности остальных состояний равны нулю.

Если процесс в системе протекает достаточно долго, то представляет интерес предельное поведение вероятностей p_i(t) при . В ряде случаев в системе устанавливается стационарный режим, при котором существуют предельные (иначе, финальные) вероятности

В таком стационарном режиме система случайным образом переходит из состояния в состояние, но вероятности состояний не меняются, при этом каждая вероятность может быть истолкована как относительное время пребывания системы в данном состоянии.

Стационарный режим возможен, конечно, только в эргодической системе или для эргодического подмножества ее состояний, при условии, что потоки событий, изменяющие состояния системы, стационарны.

Финальные вероятности состояний (если они существуют), описываются системой линейных алгебраических уравнений, получаемой из дифференциальных уравнений Колмогорова, если приравнять производные нулю. Для ТУ, рассмотренного ранее, уравнения имеют вид:

Использование нормирующего условия при этом обязательно.

7.2. Схема гибели и размножения

На практике часто встречаются системы, граф состояний которых имеет вид, показанный на рис.7.3. Здесь все состояния вытянуты в одну линию, причем каждое из них, кроме крайних, связано прямой и обратной связью с двумя соседними. Такая схема называется схемой гибели и размножения. Это название заимствовано из биологических задач, где состояния sk популяции S означает наличие в ней k единиц.

Примером может служить техническое устройство (ТУ), состоящее из нескольких одинаковых узлов, (или цеховой участок однотипных станков), которые могут заменять друг друга. Для работы ТУ достаточно, чтобы работал хотя бы один узел. При выходе из строя некоторых узлов ТУ продолжает

. . .

. . .

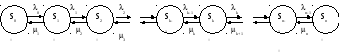
Рис. 7.3.

функционировать (возможно, менее эффективно) за счет работы остальных. При выходе из строя узла, он сразу же начинает ремонтироваться. Введем обозначения состояний ТУ:

s₀- исправны все узлы,

s₁- неисправен (ремонтируется) один узел, остальные исправны,

s_k- неисправны k узлов,

s_m- неисправны все m узлов.

На рис.7,3 интенсивности “размножения” неисправностей обозначены буквами  и проставлены у стрелок, ведущих слева на право, а интенсивности ремонтов, обозначенные буквами  - у стрелок, ведущих справа налево. Индексы обозначают состояния, которые покидает система.

Если в примере с ТУ поток отказов каждого из узлов простейший с интенсивностью , то ₀ = m, ₁ = (m-1) и т.д. Если время ремонта одного узла показательное с параметром , то ₁ = , ₂ = 2 ,..., _m = m.

Дифференциальные уравнения Колмогорова, описывающие схему гибели и размножения, имеют следующий вид.

1<k<m. (7.5)

Приравняв производные нулю, найдем финальные вероятности:

(7.6)

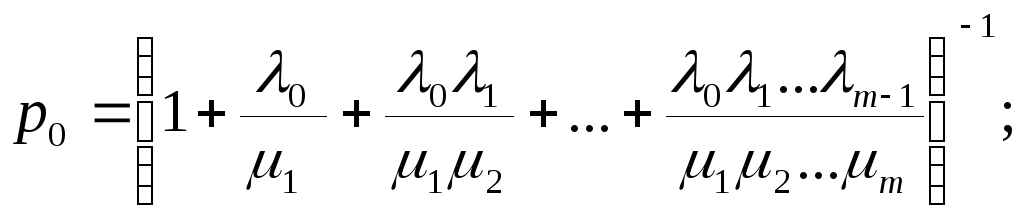
Легко заметить правило вычисления вероятности любого состояния (кроме крайнего левого): вероятность любого состояния в схеме гибели и размножения равна вероятности крайнего левого состояния, умноженной на дробь, в числителе которой стоит произведение всех интенсивностей “размножения”, стоящих левее данного, а в знаменателе - всех интенсивностей “гибели”, стоящих также левее данного.

7.3. Математическое ожидание численности популяции

Рассмотрим случайную функцию X(t) - число единиц элементов (станков и т.п.) в системе, описываемой схемой гибели и размножения. Математическое ожидание этой функции в момент времени t равно

Дифференцируя это выражение, найдем

Подставляя сюда (7,5) и приводя подобные члены, получим дифференциальное уравнение

(7.7)

Здесь следует полагать _m=₀ = 0.

Применим полученное уравнение для решения следующей задачи [5]. Производственная информация накапливается и хранится в базе данных ЭВМ. Интенсивность пуассоновского потока поступления единиц информации в базу данных равна (t) и не зависит от того, сколько их уже накоплено. Принятая на хранение, единица информации, хранится некоторое время, после чего по определенному признаку исключается. Поток исключений для каждой единицы информации - пуассоновский с интенсивностью (t).

Дифференциальное уравнение (7,7) для математического ожидания числа единиц информации, находящихся в базе данных, принимает вид

Учитывая, что , получаем

Если интенсивности пополнения и исключения информации постоянны, то при начальном условии mx (0) = m0, решение уравнения имеет вид

В стационарном режиме

Сведения о дисперсии численности популяции можно найти в [5].

7.4. Циклический процесс

Рассмотрим процесс в системе, граф состояний которой изображен на рис. 7.4. Соответствующие дифференциальные уравнения таковы

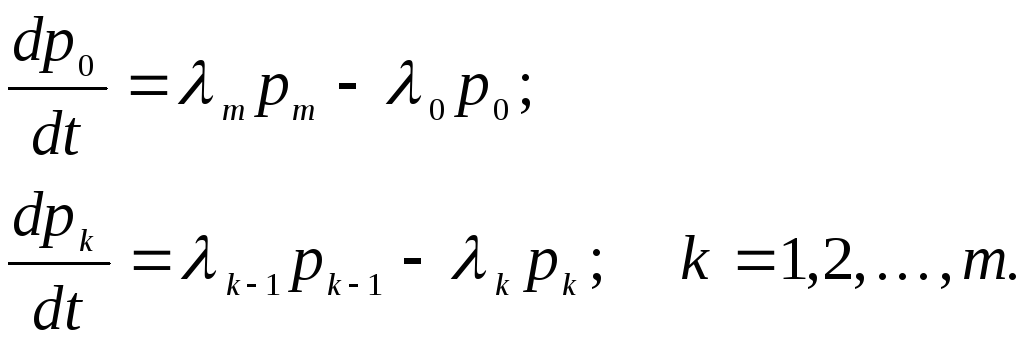
Финальные вероятности состояний в стационарном режиме найдутся из системы:

Отсюда

Рис. 7.4.

Из условия нормировки определяется p0

Примером циклического процесса может служить регулярно повторяемая транспортная или технологическая операция.