29

Глава 3.Моделирование непрерывных случайных величин

Толщина листового проката, ошибка любого измерения, стартовая масса ракеты - все это примеры непрерывных случайных величин. Их однозначное и полное определение дается законом распределения в виде функции или плотности распределения. В некоторых случаях закон распределения может быть получен теоретически (пример приведен в 6.2.), в других случаях закон распределения устанавливается экспериментально. Так на рис. 3.1 приведен полигон распределения толщины полки прессованного профиля из сплава Д16Т и выравнивающая кривая нормального закона. Данные получены автором [2] по результатам обмеров более 1000 образцов.

Прежде чем рассматривать моделирование непрерывных случайных величин на ЭВМ, напомним некоторые положения теории вероятностей.

3.1. Функции случайных аргументов

Рассмотрим функцию. Если аргумент функции – случайная величина, то и функция тоже величина случайная. Задача состоит в том, чтобы по известному закону распределения аргумента найти закон распределения функции.

Рассмотрим случай монотонно возрастающей функции . Рис. 3.2 иллюстрирует существо задачи и ее решение, основанное на равенстве площадей. Введем в рассмотрение функцию , обратную функции . Теперь функцию распределения случайной величины найдем при помощи следующей цепочки очевидных равенств:

Для определения плотности распределения f(y) необходимо определенный интеграл в полученном выражении продифференцировать по параметру y:

Этот результат легко обобщить на случай монотонно убывающей функции:

Напомним, что для вычисления математического ожидания Y закон ее распределения определять не нужно.

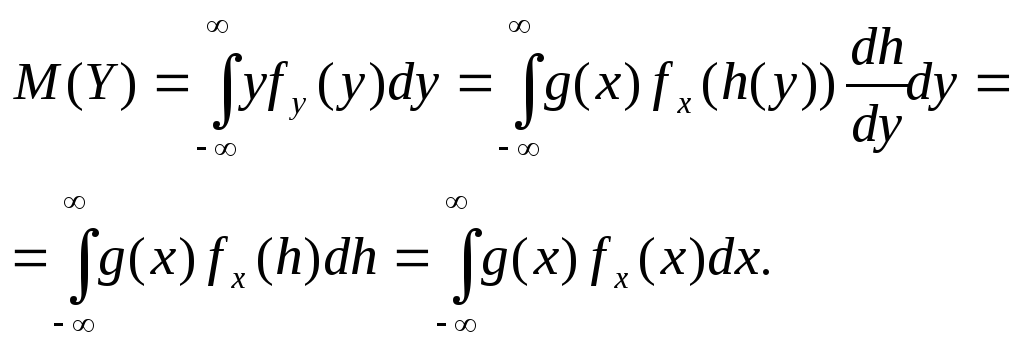
3.2. Метод обращения функции распределения

Рассмотрим алгоритм генерирования непрерывной случайной величины с заданным законом распределения, основанный на материале предыдущего параграфа.

Пусть случайная величина задана плотностью распределения . Функция ее распределения . Обозначим Введем также обратную функцию . Отметим, что вероятность неравенства < x, совпадает с функцией распределения

Теперь найдем функцию распределения случайной величины Y, учитывая, что функция неубывающая (см. рис. 3.3)

Соответствующая плотность распределения

при 0 < y <1 и 0 при других значениях.

Итак, если случайная величина распределена с плотностью, то случайная величина распределена равновероятно в интервале (0,1). Поскольку функции и монотонны, справедливо и обратное утверждение: если случайная величина распределена равновероятно в интервале (0,1) и есть функция обратная функции распределения случайной величины , то распределена с плотностью. Действительно

Следовательно, алгоритм моделирования непрерывной случайной величины с произвольным законом распределения, для которого известна функция обратная функции распределения , состоит в следующем:

1) генерируется реализация r базовой случайной величины R, распределенной равномерно в интервале (0,1);

2) определяется реализация случайной величины X из соотношения

Рассмотрим несколько примеров.

Известно, что длительность нормальной работы электронной аппаратуры между двумя ремонтами имеет экспоненциальное распределение

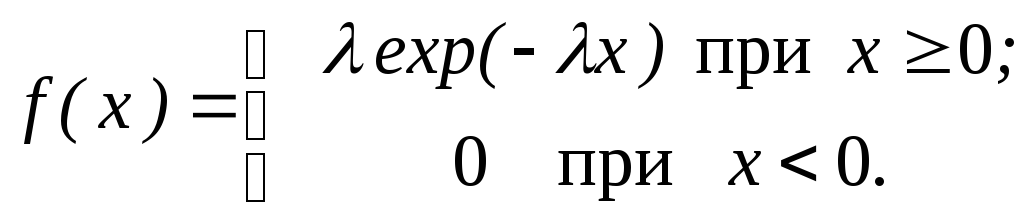
Здесь - среднее число отказов в единицу времени. Соответствующая функция распределения

Положим , отсюда . Следовательно, генератор экспоненциально распределенной случайной величины должен использовать следующее соотношение между случайной величиной X и базовой случайной величиной R

2. Рассеивание точек падения по дальности Y и боку Z при стрельбе снарядами распределены нормально. Если средние квадратичные отклонения по дальности и боку одинаковы и равны σ,то расстояние X от центра группирования до точки падения распределен по закону Рэлея

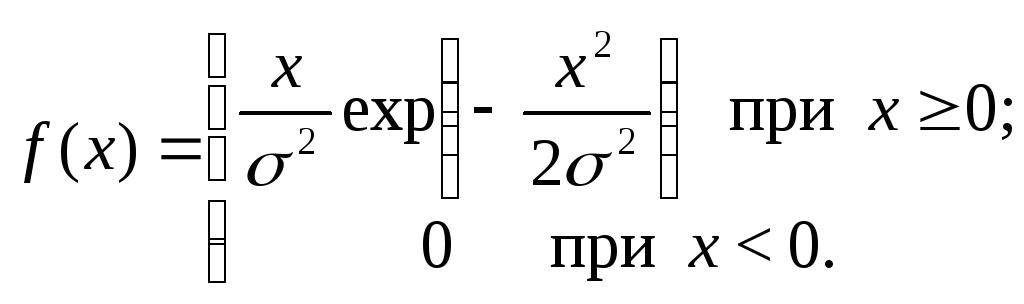
Соответствующая функция распределения

Следовательно, генератор случайной величины, распределенной по закону Рэлея, должен использовать соотношение

соответствующая программа на Фортране может иметь вид

Subroutine Ralay (S, Ix, Iy)

call Randu(Ix, Iy, R)

X= S*sqrt(-2.0*alog(R))

return

end

3.3. Нормальное распределение

Нормально распределенные случайные величины встречаются чаще других из-за того, что случайность - это обычно проявление многих одновременно действующих причин, и, следовательно, характер закона распределения подчиняется центральной предельной теореме. Пример нормального распределения толщины проката приведен на рис 3.1.

Плотность вероятности нормального распределения описывается выражением

Здесь - математическое ожидание и среднее квадратическое отклонение случайной величины.

К сожалению, функция распределения и обратная ей функция не могут быть выражены аналитически, поэтому метод, рассмотренный в 3.2, оказывается непригодным. Задача, тем не менее, может быть решена приближенно, если использовать подходящую аппроксимацию обратной функции. Например, случайная величина

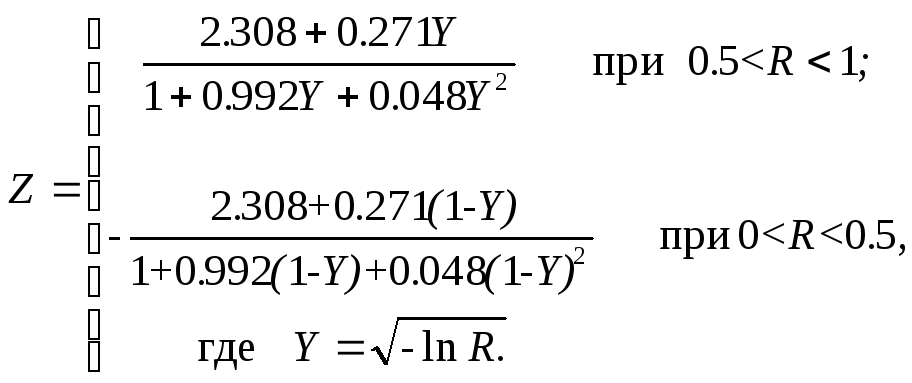
распределена приблизительно нормально с нулевым математическим ожиданием и дисперсией, равной единице. Как и раньше R равновероятна в интервале (0, 1). Следовательно, для Х имеем

Другой способ моделирования нормального распределения основан на применении центральной предельной теоремы. Если n случайных величин независимы и распределены равновероятно в интервале (0,1), то распределение случайной величины

тем ближе к нормальному, чем больше n, а математическое ожидание и дисперсия соответственно равны 0 и 1. Часто достаточно положить n=12, тогда

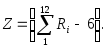
Соответствующая программа на Фортране имеет вид.

Subroutine Gauss(Ix, S, E, X)

A=0.0

do i = 1, 12

call Randu(Ix, Iy, R)

A= A + R

end do

X = E + S*(A - 6.0)

return

end

Входные параметры подпрограммы E и S - математическое ожидание и среднее квадратическое отклонение случайной величины X.

Этот вариант имеет малую точность за пределами . Пределы могут быть расширены до , если “хвосты” распределения подкорректировать следующим образом

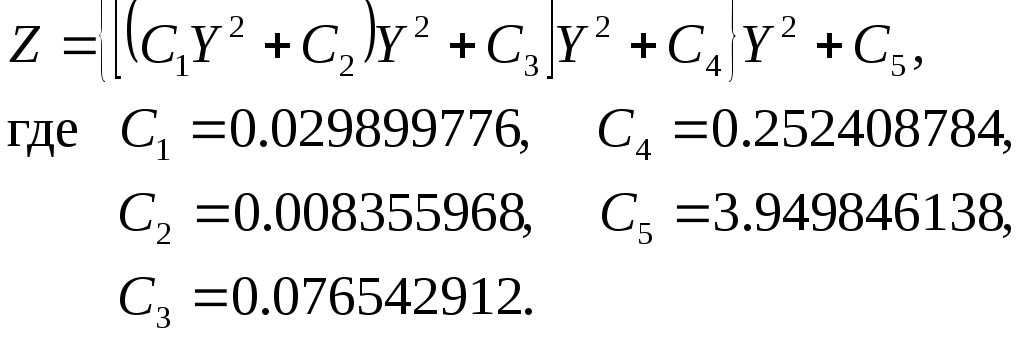
3.4. Метод Неймана

М

Нет

Да

етод Неймана или иначе метод исключения относится к числу универсальных, не накладывающий на моделируемый закон распределения жестких ограничений, как, например, первый из рассмотренных. Для применения этого метода достаточно двух условий:

1) интервал (a, b), на котором распределена случайная величина - конечен;

2) плотность распределения ограничена сверху

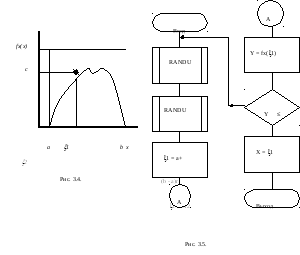
На плоскости (рис. 3.4) выделим прямоугольник с основанием (ab) и высотой c. Пусть точка М случайна и имеет равномерное распределение внутри этого прямоугольника. Для этого координаты точки должны быть независимы и иметь равномерное распределение в интервалах (a,b) и (0, c).

Алгоритм моделирования (см. блок-схему на рис. 3.5) состоит в следующем.

1. Генерируются две реализации базовой случайной величины .

Выполняются преобразования:

3. Вычисляется значение плотности вероятности моделируемого распределения

4. Выполняется сравнение Если , осуществляется возврат к п.1, иначе значение принимается в качестве реализации случайной величины X.

Несложное доказательство справедливости алгоритма состоит в следующем. Рассмотрим событие А, состоящее в том, что в одиночном испытании точка М окажется под кривой плотности распределения, т.е. Вероятность события A равна отношению площадей:

Условная вероятность события А, вычисленная при определенном значении , равна отношению отрезков: Следовательно, плотность условного распределения при условии, что точка М находится под кривой плотности распределения совпадает с плотностью моделируемого распределения:

Здесь - плотность распределения .

3.5. Точность косвенных измерений