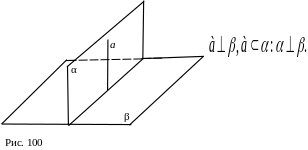
Признак перпендикулярности плоскостей

Если одна из плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны [5, с.49], [10, с. 33].

1.4. Дополнительный признак перпендикулярности прямых

Т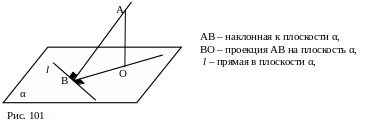 еорема о трёх перпендикулярах: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна к её проекции на эту плоскость, то она перпендикулярна и к самой наклонной [5, c. 42], [10, c. 31].

Справедлива и обратная теорема: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна к ней, то она перпендикулярна и к её проекции [5, c. 42], [10, c.31 ].

Обобщённая теорема о трёх перпендикулярах: любая прямая на плоскости, перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и наклонной [10, задача 33, с. 62].

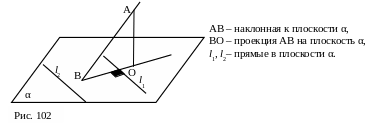
Справедлива и обратная теорема: любая прямая на плоскости, перпендикулярная наклонной к этой плоскости, перпендикулярна и её проекции.

1.5. Дополнительные признаки перпендикулярности прямой и плоскости

1. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости [5, с. 35], [10, с. 28].

Рис. 103

2. Если прямая перпендикулярна к одной из параллельных плоскостей, то она п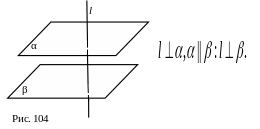 ерпендикулярна и к другой плоскости [5, с.40, задача 132], [8, с. 17].

3. Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она перпендикулярна и другой плоскости [10, стр. 41, задача 58].

4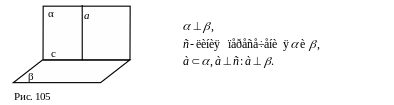 . Линия пересечения двух плоскостей, перпендикулярных к третьей плоскости, есть перпендикуляр к этой плоскости [8 ,c. 24].

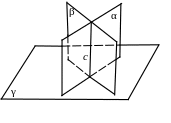
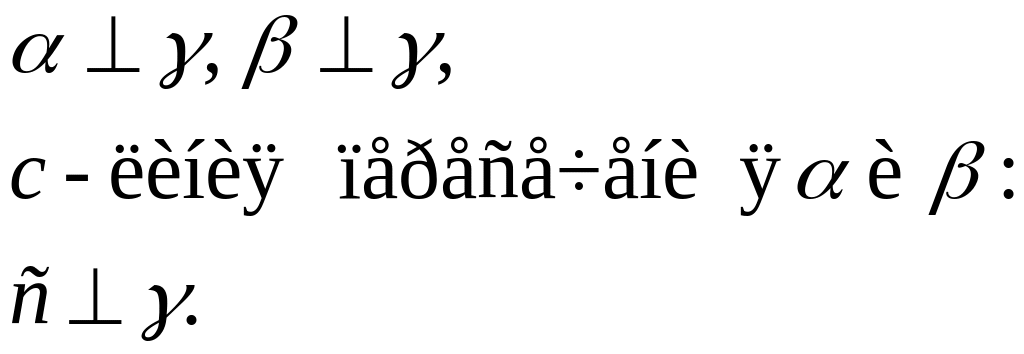
Рис. 106

1.6. Дополнительные признаки перпендикулярности плоскостей

1. Плоскость, перпендикулярная к прямой, по которой пересекаются две 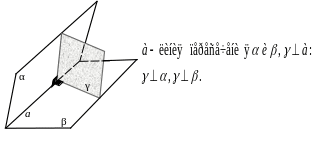данные плоскости, перпендикулярна к каждой из этих плоскостей [5, с. 49].

Рис. 107

2. Если две плоскости параллельны и одна из них перпендикулярна к третьей плоскости, то и вторая перпендикулярна к ней.

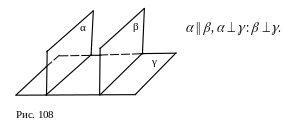
2. Доказательства утверждений теоретической карты №2

2.1. Перпендикулярность прямых

Доказательство признака перпендикулярности прямых (1) приводится в учебнике Атанасяна [5,с. 34].

Доказательство признака перпендикулярности прямых (2) приводится в учебнике Погорелова [10, с.25]

2.2. Перпендикулярность прямой и плоскости

Доказательство признака перпендикулярности прямой и плоскости приводится в учебниках [5, с. 36], [10, с. 26].

2.3. Перпендикулярность плоскостей.

Доказательство признака перпендикулярности плоскостей приводится в учебниках [5, с.49], [10, с. 33].

2.4. Дополнительный признак перпендикулярности прямых

Доказательство теоремы о трёх перпендикулярах приводится в учебниках

[5, c. 42], [10, c. 31]. Обобщённая теорема доказана в учебнике [10, задача 33, с. 50].

2.5. Дополнительные признаки перпендикулярности прямой и плоскости

Доказательство первого дополнительного признака перпендикулярности прямой и плоскости приводится в учебниках [5, с. 35], [10, с. 28].

Приведём доказательство второго дополнительного признака перпендикулярности прямой и плоскости [5, с.40, задача 13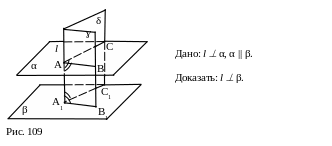2].

2.

Дополнительные построения

1. Построим любую плоскость АВ – линия пересечения А₁В₁ – линия пересечения

2. Построим любую плоскость АС – линия пересечения А₁С₁ – линия пересечения

Доказательство

1. ÐBAA₁=90°, так как l ^ α.

2. АВ || A₁B₁, так как α || β, тогда ÐBAA₁=ÐA A₁B₁=90°.

3. Аналогично ÐA A₁С₁=90°.

4. Из (1) и (2) следует, что l ^ β.

Ниже приведено доказательство третьего дополнительного признака

п

Рис. 110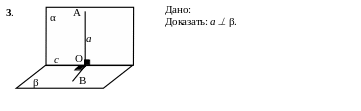

ерпендикулярности прямой и плоскости.

Доказательство.

Дополнительные построения.

Пусть АО  другое обозначение прямой а, где О – точка пересечения прямых а и с. Проведём в плоскости β прямую ОВ ^ с.

1. ÐАОВ – линейный угол двугранного угла, образованного перпендикулярными плоскостями α и β. ÐАОВ=90°.

2. АО^с ( по условию) и АО^ОВ ( пункт 1), следовательно АО  β.

4.Доказательство четвёртого дополнительного признака перпендикулярности плоскостей приведено в учебнике [5, с. 49].