3.4. Дополнительные признаки параллельности прямых

№ 37 (устно). SABCD – правильная пирамида. Как построить линию пересечения плоскостей граней SAD и SBC, SAB и SDC? Ответ обосновать.

№ 38 (устно). Изобразить параллелограмм ABCD и точку Р, не лежащую в плоскости этого параллелограмма. Отметить точки E, K, M, H – середины сторон AB, BC, CD и AD соответственно. Как построить линию пересечения плоскостей PEH и PKM? Ответ обосновать.

№ 39 (устно). АВСDA₁B₁C₁D₁ - куб. Как построить линию пересечения плоскости DA₁C₁ и плоскости грани АВС? Ответ обосновать.

№ 40 . Основание пирамиды SABCD – трапеция ABCD. Построить сечение пирамиды плоскостью, проходящей через ребро AD и точку М, принадлежащую грани BSC.

План построения.

1. KN || BC, МKN.

2. AK.

3. ND.

4. AKND – сечение.

5. Доказать, что сечение искомое.

Рис. 70

№ 41. Треугольники ABC и DBC не лежат в одной плоскости и имеют общую сторону, точки М, Н и К – середины соответственно сторон BD, CD, AC. 1) Построить l линию пересечения плоскостей МКН и АВС. 2) Построить точку Р пересечения плоскости МКН и прямой АВ. 3) Найти РК, если ВС=8.

4) Доказать, что отрезки РН и МК пересекаются и в точке пересечения делятся пополам.

1 . 2. 3.4.

1) План построения. 3)

1. Прямая l: l ABC, Kl, l || BC. 1. PK– средняя линия BAC.

2. Доказать, что l – искомая линия 2. PK=4.

пересечения плоскостей. 4)

2) План построения. 1.KH – параллелограмм,

1. P= l  AB. MK, PH – диагонали.

2. Доказать, что Р – искомая точка 2. Вывод.

пересечения прямой и плоскости.

№ 42. Треугольник APD и трапеция ABCD имеют общую сторону AD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка PD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если AD = 10.

План решения.

1. l – линия пересечения плоскостей

BCK и PAD.

l ADP, Kl, l || AD.

2. M – точка пересечения прямой АР

и плоскости ВСК.

3. МК – средняя линия APD, MK=5.

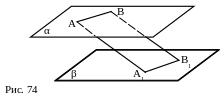
№ 43 (устно). Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны. Доказать по рисунку 74.

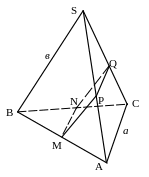
№ 44. В правильной треугольной пирамиде SABC сторона основания а и боковое ребро в. Провести в этой пирамиде плоскость через середины рёбер АВ и ВС параллельно ребру SB. Определить периметр полученного сечения.

План построения.

1. MN.

2. MPSAB, MP || SB.

3. NQBSC, NQ || SB.

4. PQ.

5. MNQР – сечение.

6. Обосновать построение сечения.

План вычисления.

1

Рис. 75

. MN. 2. MP. 3. P_MNQP.

Ответ:

№ 45. Построить сечение правильной четырёхугольной пирамиды, проходящее через середины двух смежных сторон основания и середину высоты. Вычислить периметр полученного сечения, если каждое ребро пирамиды равно а.

План построения.

Пусть точки K, F – середины смежных сторон АВ и ВС основания пирамиды,

Р  середина высоты .

1. KF.

2. В плоскости ASC через точку Р

построить MN || AC (рис. 76).

3. Q = KF  BD.

4. QP. 5. L = QP  SD (рис. 77).

6. Обосновать, что KMLNF–

искомое сечение (рис. 78).

План вычисления.

1. KF. 2. MK. 3. LQ. 4. LP. 5. Вид  MLN. 6. Вид  LPN. 7. PN. 8. LN. 9. P_KMLNF.

Ответ:

№46 (устно). Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершины А, С и точку М ребра A₁B₁.

1. MP || A₁C₁.

2. АМРС – искомое сечение.

3.Обосновать, что АМРС–

искомое сечение (рис. 79).

Рис. 79

№ 47 (устно). Через вершину тетраэдра проведена плоскость, параллельная противолежащей грани. Как построить линии пересечения этой плоскости с плоскостями остальных граней тетраэдра?

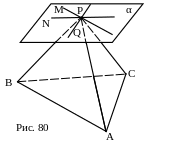
Назвать линии пересечения плоскости α с гранями BPA, APC, BPC и обосновать выбор.

№ 48. В кубе ABCDA₁B₁C₁D₁ середины К и L противолежащих рёбер АА₁ и СС₁ соединены отрезками прямых с вершинами куба В и D₁. Определить вид получившегося четырёхугольника KBLD₁ и найти его стороны и диагонали. Ребро куба равно а.

Ответ:

ромб;

№ 49. В правильной четырехугольной призме ABCDA₁B₁C₁D₁ AB=1, AA₁=4. Построить сечение призмы, параллельное АС и проходящее через точки D₁ и К – середину AA₁. Вычислить площадь полученного сечения.

План построения.

1. КК₁ || АС.

2. D₁K.

3. D₁K₁.

4. l: l || D₁K₁, K  l, KB.

5. p: p|| D₁K, K₁ p, K₁B.

6. Обосновать, что D₁KBК₁ – искомое

сечение.

План вычисления.

1. Вид сечения.

2. КК₁. 3. D₁В. 4. S .

Ответ: 3.

№ 50. Основанием правильной призмы служит шестиугольник со стороной 3 дм; высота призмы равна 13 дм. Определить площадь сечения, проведённого через две противолежащие стороны верхнего и нижнего оснований призмы.

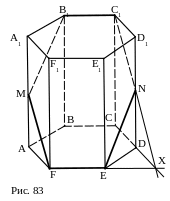
План построения.

1. Х – точка пересечения прямой FE и плоскости грани СС₁DD₁.

2. C₁Х, точка N.

3. MF || C₁N.

4. EN.

5. MB₁ || EN.

6. Обосновать, что FMB₁C₁NE – искомое сечение.

План вычисления.

1. =2S_FMNE.

2. MN. 3. NE. 4. PN. 5. PE. 6. S_FMNE.

7. Ответ: 63 дм².

№ 51. На параллельных плоскостях α и β выбрано по паре точек А₁, А₂ и В₁, В₂ соответственно так, что прямые А₁В₁ и А₂В₂ пересекаются в точке S. Вычислить SA₁ и SB₂, если А₁В₁=6 см, SA₂=2,5 см SB₂ : SA₂=3.

П лан решения.

1.  SB₁B₂ ~  SA₁A₂.

2. Коэффициент подобия.

3. SB₂.

4. Выразить SA₁через SB₁.

5. SA₁.

Ответ: 1,5 см; 7,5 см.

Рис. 85

Рассмотреть иное расположение заданных геометрических фигур (рис. 86) и решить задачу для второго случая.

Ответ: 3 см и 7,5 см.

№ 52. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А₁, В₁ и С₁, а другую – в точках А₂, В₂ и С₂. Докажите, что треугольники А₁В₁С₁ и А₂В₂С₂ подобны.

У казание.

Доказать пропорциональность сторон

треугольников А₁В₁С₁ и А₂В₂С₂ или равенство их углов.

Рассмотреть иное расположение заданных геометрических фигур и решить задачу для второго случая.

Рис. 87

№ 53. В правильной треугольной пирамиде SABC через SD и СЕ, где D – середина АВ, Е – середина SA проведены сечения пирамиды, параллельные между собой. Определить площадь большего из них, если площадь меньшего равна Q.

План построения.

1. ME || SD.

2. MC.

3. DР || MC.

4. SР.

5. SDР || EMC.

План вычисления.

1. SDР = EMС = . 2. Выразить площадь  SDР через SD, DР и .

3. Выразить SD через ME. 4. Выразить DР через MC.

5. Выразить площадь  SDР через ME, MC и  .

6. Выразить площадь  SDР через площадь  MEC. Ответ:

II. Перпендикулярность в пространстве

1. ТЕОРЕТИЧЕСКАЯ КАРТА №2

1.1 Перпендикулярность прямых

Определения

1 . Две прямые называются перпендикулярными, если они пересекаются под прямым углом [10, c. 25].

Рис. 89

2. Скрещивающиеся прямые называются перпендикулярными, если угол между ними равен 90 [10, c.50].

(Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым [10, c. 50]).

3. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°[5, c. 34].

Рис. 91

Признаки перпендикулярности прямых

1. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой [5, с. 34].

2. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они перпендикулярны [10, с.25].

1.2. Перпендикулярность прямой и плоскости

Определения

1. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости [10, c.34].

2. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения [10,с. 26].

Признак перпендикулярности прямой и плоскости

1. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости [5, с. 36], [10, с. 26].

1.3. Перпендикулярность плоскостей

Определения

1. Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым [10, с. 32].

2 . Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90° [5, с.52]. (Определение угла между плоскостями приведено на странице 73).