3 N .3.Параллельность плоскостей

№ 26 (устно). Верно ли утверждение, что если плоскости α и β параллельны и прямая а лежит в плоскости α, то эта прямая параллельна плоскости β (рис. 47).

№ 27 (устно). Доказать, что 1) противоположные грани параллелепипеда параллельны; 2) сечения параллелепипеда, проходящие через тройки его вершин А, В₁, С и А₁, С₁, D, параллельны между собой. Сколько пар таких сечений можно провести?

№ 28 (устно). Если две параллельные прямые одной плоскости параллельны двум прямым другой плоскости, то будут ли эти плоскости параллельны?

Рис. 50

№ 29 (устно). Верно ли утверждение: если две прямые, лежащие в одной плоскости, параллельны другой плоскости, то эти плоскости параллельны?

№ 30 (устно). Основание призмы - трапеция. Доказать, что призма имеет только одну пару параллельных боковых граней.

С₁

В₁

D₁

А₁

B

C

А

D

Рис. 52

№ 31 (устно). Дан тетраэдр DABC. Точки М, N, P являются серединами ребер DA, DB, DC. Доказать, что плоскости MNP и ABC параллельны.

№ 32 (устно). Две стороны треугольника параллельны плоскости α. Доказать, что и третья его сторона параллельна плоскости α.

№ 33. Три отрезка А₁А₂, В₁В₂ и С₁С₂, не лежащие в одной плоскости, имеют общую середину. Доказать, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны.

План доказательства.

1. A₁OB₁=A₂OB₂.

2. A₁B₁|| A₂B₂.

3. A₁OC₁=A₂OC₂.

4. A₁C₁|| A₂C₂.

5. Вывод.

В задачах №34 №35 выбираются два отрезка, лежащие на скрещивающихся прямых.

№ 34. Дана правильная треугольная пирамида. Построить два её параллельных сечения, проходящих через:

1 ) среднюю линию основания и среднюю линию боковой грани;

План построения.

MN, РQ – средние линии

1. МК || AD.

2. КN.

3. Плоскости MKN и ADC параллельны.

2) апофему и среднюю линию боковой грани;

План построения.

MN – средняя линия грани ADC,

DQ – апофема.

1. NP || DQ.

2. PM.

3. QC ||PM.

4. Плоскости PNM и QDC параллельны.

3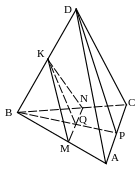 ) среднюю линию основания и медиану боковой грани;

План построения.

MN – средняя линия грани AВC,

DР –медиана боковой грани ADC.

1. ВDP.

2. Q – точка пересечения MN и BP.

3. QK || DP.

4. MKN.

Рис. 58

5.Плоскости MKN и ADC параллельны.

4) медианы двух боковых граней;

План построения.

DM –медиана боковой грани ADC,

АК – медиана боковой грани AВD

1. BDM.

2. KP || DM.

3. AP.

4. Q – точка пересечения АР и ВС.

5. QK.

6. MN || AQ.

7. DN.

8. Плоскости КАQ и DMN параллельны.

5) высоту пирамиды и среднюю линию боковой грани;

План построения.

MN – средняя линия грани ADC,

DО – высота пирамиды.

1. APD.

2. NQ ||DO.

3. MQ.

4. K – точка пересечения

5. KN. 6. DE || NK. 7. EC

8.Плоскости KNM и DEC параллельны.

6 ) высоту пирамиды и медиану боковой грани.

План построения.

DO – высота пирамиды,

ВN – медиана боковой грани.

1. DAM.

2. NK || DO.

3. ВК.

4. F – точка пересечения ВК и АС.

5. FN.

6. QP || BF, OQP.

7. DQ.

8. Плоскости ВNF и DQP – параллельны.

№ 35. Пусть АВСDA₁B₁C₁D₁  куб. Построить два его сечения, параллельных между собой и проходящие через:

1 ) АС и В₁D₁;

План построения.

1. А₁С₁.

2. BD.

3. Плоскости граней ABCD и A₁B₁C₁D₁

параллельны.

2) АС и С₁D;

План построения.

1. АВ₁. 2. В₁С.

3. А₁С₁. 4. А₁D.

5. Плоскости АСВ₁ и С₁DА параллельны.

3) АС и В₁D;

План построения.

1. OK ||B₁D.

2. AK. 3. KC.

4. MN || AC.

5. Q – точка пересечения MN и В₁D.

6. MB₁. 7. B₁N. 8. ND. 9. DM.

10.Плоскости треугольника АКС и четырёхугольника MB₁ND параллельны.

4) АС и О₁О₂, где О₁ и О₂ – центры граней

АА₁В₁В и А₁В₁С₁D₁.

План построения.

1.А₁С₁. 2. А₁В. 3. С₁В.

4. АС. 5. АD₁. 6. CD₁.

7. Плоскости А₁С₁В и АСD₁

параллельны.

№ 36. В правильном тетраэдре с ребром а DO – высота тетраэдра. Точка М – середина DO. 1) Провести через точку М сечение, параллельное плоскости ACD. 2) Вычислить периметр и площадь сечения.

План построения.

1. P – точка пересечения ВО и АС.

2. Плоскость BDP.

3. RQ || DP, MRQ.

4. KN || AC, Q KN.

5. RK.

6. RN.

7. Сечение KRN параллельно грани ADC.

2) 1.  KRN ~  ADC. 2. Коэффициент подобия k=RQ : DP. 3. Р_АDC.

4. Р_KRN. 5. S _АDC. 6. S_KRN.

Ответ: